
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантово-механические операторыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопросы: 1 Линейные операторы. 2 Коммутативные операторы. 3 Самосопряжённые (эрмитовы) операторы. 4 Основные квантово-механические операторы.
Принятые обозначения: · · · · · · ·
Основные формулы: · Оператор
· Операторы
· Оператор
где · Оператор проекции и квадрата импульса:
· Оператор полной энергии (гамильтониан):
· Оператор проекции момента импульса:
· Оператор квадрата момента импульса:
Задачи
1 Проверить следующее операторное равенство: 2 Найти результат действия операторов 3 Найти собственное значение оператора 4 Найти собственные функции 5 Проверить следующие правила коммутации: 6 С помощью правил коммутации, приведенных в предыдущей задаче, показать, что: Ответы
2. Уравнение Шредингера
Вопросы: 1 Временное уравнение Шредингера. 2 Стационарное уравнение Шредингера 3 Уравнение Шредингера в операторной форме 4 Стандартные условия, накладываемые на волновую функцию.
Принятые обозначения: · · · · · · · · ·
Основные формулы: · Временное уравнение Шредингера:
· Стационарное уравнение Шредингера:
если потенциал · Вероятность обнаружить частицу в интервале от x1 до x2:
· Оператор Лапласа в сферических координатах для функции
· Коэффициент прозрачности прямоугольного потенциального барьера конечной ширины:
где
Задачи
1 Написать уравнение Шредингера для: а) электрона, находящегося в водородоподобном атоме; б) линейного гармонического осциллятора. 2 Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины 3 Электрон наводится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы такова, что энергетические уровни расположены весьма густо. Найти плотность уровней 4 Электрон находится в одномерном потенциальном ящике шириной 5 6 Волновая функция частицы массы 7 Определить энергию электрона атома водорода в стационарном состоянии, для которого волновая функция 8 Волновая функция электрона в основном состоянии атома водорода имеет вид 9
Ответы
2.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.25.14 (0.008 с.) |

 – произвольная функция.
– произвольная функция. − оператор импульса.
− оператор импульса.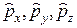 − операторы проекции импульса на оси координат.
− операторы проекции импульса на оси координат. − оператор полной энергии.
− оператор полной энергии.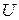 – потенциальная энергия.
– потенциальная энергия.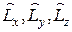 − операторы проекций момента импульса на оси координат.
− операторы проекций момента импульса на оси координат.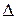 − оператор Лапласа.
− оператор Лапласа.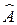 линейный, если:
линейный, если: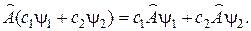
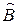 коммутативны, если их коммутатор:
коммутативны, если их коммутатор:

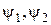 − произвольные функции.
− произвольные функции.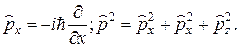
 .
.
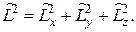
 .
.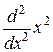 и
и 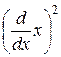 на функции: a)
на функции: a) 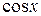 и б)
и б) 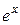 .
. , принадлежащее собственной функции
, принадлежащее собственной функции  , если:
, если: 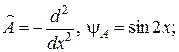


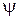 и собственные значения следующих операторов:
и собственные значения следующих операторов: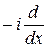 , если
, если 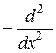 , если
, если 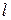 .
.


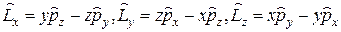 и
и 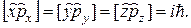
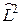 коммутирует с операторами
коммутирует с операторами 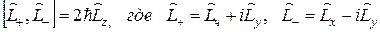 .
.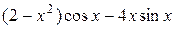 ;
;  ;
;  ;
; 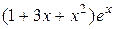 . 3. 4; 1;
. 3. 4; 1;  . 4.
. 4. 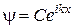 , где
, где 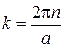 ,
, 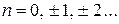 ;
; 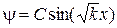 , где
, где  ,
, 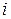 – мнимая единица,
– мнимая единица, 
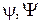 − волновая функция, описывающая состояние частицы.
− волновая функция, описывающая состояние частицы.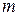 − масса частицы.
− масса частицы.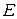 – полная энергия частицы.
– полная энергия частицы.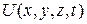 – потенциальная функция координат и времени.
– потенциальная функция координат и времени.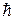 − постоянная Планка.
− постоянная Планка. − оператор Лапласа.
− оператор Лапласа. – вероятность.
– вероятность. – коэффициент прозрачности.
– коэффициент прозрачности.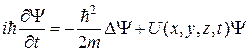 .
.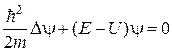 ,
,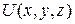 не зависит от времени.
не зависит от времени.

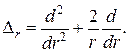
 ,
,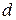 − ширина барьера.
− ширина барьера.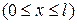 . Найти вероятность пребывания частицы в области
. Найти вероятность пребывания частицы в области 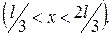 .
.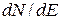 , т.е. их число на единичный интервал энергии, в зависимости от
, т.е. их число на единичный интервал энергии, в зависимости от 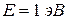 , если ширина ямы равна 1 см.
, если ширина ямы равна 1 см. электрона, если
электрона, если 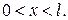
 Частица массы
Частица массы 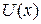 , вид которого показан на рисунке 2, где
, вид которого показан на рисунке 2, где  . Найти:
. Найти: 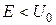 , привести это уравнение к виду:
, привести это уравнение к виду: 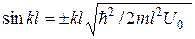 , где
, где 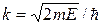 . Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы образуют дискретный спектр;
. Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы образуют дискретный спектр; 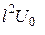 , при котором появляется первый энергетический ypoвeнь в области
, при котором появляется первый энергетический ypoвeнь в области 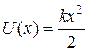 имеет вид
имеет вид  , где
, где  − нормировочный коэффициент,
− нормировочный коэффициент, 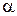 − положительная постоянная. Найти с помощью уравнения Шредингера постоянную
− положительная постоянная. Найти с помощью уравнения Шредингера постоянную 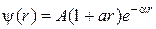 , где
, где 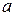 и
и 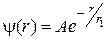 , где
, где  − первый боровский радиус. Найти:
− первый боровский радиус. Найти:  Электрон с энергией
Электрон с энергией  движется в положительном направлении оси
движется в положительном направлении оси  (смотри рисунок 3). Высота U потенциального барьера равна 5 эВ. При какой ширине d барьера вероятность
(смотри рисунок 3). Высота U потенциального барьера равна 5 эВ. При какой ширине d барьера вероятность 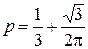 . 3. 0,8 107 уров/эВ. 4.
. 3. 0,8 107 уров/эВ. 4.  . 5. б)
. 5. б) 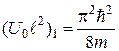 . 6.
. 6.  ;
;  7.
7.  . 8. rвф=r1;
. 8. rвф=r1; 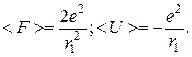 9.» 0,5 нм.
9.» 0,5 нм.


