
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операторы цикла и условные операторыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Язык ML имеет специальные управляющие конструкции, которые позволяют задавать последовательность выполнения команд в программах. Такие конструкции называются операторами управления и задаются с помощью ключевых слов. Это операторы цикла for и while, условный оператор if и оператор переключения (выбора) switch…case. Синтаксис и выполняемые действия этих операторов аналогичны соответствующим операторам известных языков программирования. Область действия каждой конструкции ограничивается словом end. MATLAB допускает вложенность операторов. Оператор цикла с параметром позволяет описывать действия, которые выполняются фиксированное количество раз:
for <параметр цикла>=<начальное значение>:<шаг>:<конечное <операторы> end
Для досрочного прерывания цикла используется оператор break. Если шаг изменения параметра цикла равен единице, то его можно не указывать. Параметры цикла, их начальное и конечное значения и шаг изменения могут быть целого и вещественного типа. Например, требуется вычислить значения у=x 2 для всех х на отрезке от 1 до 10 c шагом равным 3:
>>for x=1:3:10 y=x^2 end
Результат выполнения данного оператора: y = y = y = y =
Или вычислим значения у для всех х на отрезке от 0,1 до 1
>> for x=0.1:0.5:1 y=x^2 end
В результате получили
y = 0.0100 y = 0.3600
Везде, где возможно, в ML следует использовать не циклы, Пусть требуется составить вектор из пяти нечетных чисел натурального ряда. В ML решать эту задачу можно тремя способами: Первый способ – использовать оператор цикла
>> for i =1:5 x(i)=2*i-1 end
На экране получим
x = x = 1 3 x = 1 3 5 x = 1 3 5 7 x = 1 3 5 7 9 Этот способ очень неэффективен по времени, так как память не выделяется сразу под весь массив, а при каждой итерации цикла заново создается вектор х с размерностью на единицу большей, чем на предыдущем шаге, что и приводит к большим затратам времени. Это показывает распечатка результатов. Второй способ – сформировать вектор из нулей х = zeros (1,5),
>> x=zeros(1,5) x = 0 0 0 0 0 >> for i=1:5 x(i)=2*i-1 end
В результате получим
x =
1 0 0 0 0 x = 1 3 0 0 0 x = 1 3 5 0 0 x = 1 3 5 7 0 x = 1 3 5 7 9
В данном случае мы заранее определили размер вектора, в который записываются результаты работы цикла. Этот способ несколько быстрее первого. Третий способ – можно сформировать два вектора: вектор i=1:5 и вектор х=2*i-1
>> i=1: 5 i = 1 2 3 4 5 >> x=2*i-1 x = 1 3 5 7 9
В данном случае применяются векторные операции вместо использования циклов, и этот способ самый быстрый. Чтобы повысить эффективность работы программы, следует иметь в виду следующее правило: везде, где возможно, заменять фрагменты программы, содержащие циклы for и while, на матричные операции или матричные функции. Это объясняется тем, что скорость выполнения матричных и векторных операций выше. Если нельзя обойтись без циклов, то можно заставить их выполняться быстрее, если следовать правилу: создавать заранее каждый массив, в который требуется записывать результат работы цикла. Оператор цикла с предусловием позволяет запрограммировать цикл, в котором количество повторений зависит от выполнения некоторого условия:
while <логическое выражение, задающее условие продолжения цикла> <операторы> end
Сформируем вектор нечетных чисел:
>>x=zeros(1, 5) >> i=1; >> while i<=5 x(i)=2*i-1; i=i+1; end В результате получим вектор x = 1 3 5 7 9
Как видим, такой способ получения последовательности нечетных чисел тоже возможен, но он также является неэффективным, т. е. медленным. Найти наибольшее число, факториал которого< 150:
>>echo on % нахождение наибольшего числа, факториал, которого меньше 150 >>i=1; f=1; while f<150 i=i+1; f=f*i; end disp(i-1) на экране получим
или можно воспользоваться встроенной функцией:
>> i=1; while prod(1:i)<150 i=i+1; end; disp(i-1) на экране получим
Условный оператор позволяет организовать ветвления в программе и имеет следующую синтаксическую конструкцию:
if (<логическое выражение1>) <операторы> [elseif (<логическое выражение2>) <операторы> elseif (<логическое выражение3>) <операторы> …] [else <операторы>] end
В этой конструкции может быть произвольное количество вложений ветвей elseif,или их может не быть вовсе. Пусть необходимо по введенной с клавиатуры температуре воздуха охарактеризовать погоду. Введем следующий текст:
>> t=input('введи температуру') if (t<0) s='мороз' elseif and(t>0,t<=10) s='холодно' elseif and(t>10,t<=20) s='тепло' else s='жарко' end В результате выполнения этих команд получим на экране
введи температуру (например, ввели -4) -4 t = -4 s = мороз
Логическое выражение может быть записано и в такой форме: (t>0)&(t<=10)
Оператор переключения (выбора). Если необходимо сделать множественный выбор, можно воспользоваться оператором переключения, синтаксическая конструкция которого приведена ниже:
Switch <ключевое выражение> Case { <список значений1} <операторы> Case {<список значений2>} <операторы> ……. [Otherwise <операторы>] End
Сначала вычисляется значение ключевого выражения. Затем это значение ищется в списках значений. Если совпадение найдено, то выполняются операторы соответствующего блока, в противном случае выполняются операторы, стоящие после ключевого слова otherwise. Пусть необходимо по введенному с клавиатуры номеру месяца вывести название времени года. Ниже приведены команды, позволяющие решить эту задачу:
>>n=input('введи номер месяца: ') switch n case {1,2,12} disp('зима') case {3,4,5} disp('весна') case {6,7,8} disp('лето') case {9,10,11} disp('осень') otherwise disp('ошибка') end На экране получим: введи номер месяца: 11 n = осень Встроенные функции eval и menu Функция eval. В ML имеется возможность сформировать требуемую команду в виде строки символов, а затем выполнить ее, как обычную команду, набранную в командном окне. Для этого предназначена встроенная функция eval. Метод задания команд в виде текстовых строк и их выполнения с помощью этой функции используется при написании Функция еval (<текст>) предназначена для выполнения команды, заданной текстом, как команды ML. Например, eval (‘2*2+3’) выводит на экран 7. Аргументом функции может быть также строковая переменная. Команда eval (‘<имя скрипт-файла>’) вызовет выполнение операторов, находящихся в файле с соответствующим именем. Функция menu. Эта функция предназначена для вывода на экран окна с выпадающим меню, которое имеет заголовок и кнопки с названиями пунктов меню. Количество кнопок, равное количеству пунктов меню, определяется количеством параметров функции menu:
k= menu (‘<заголовок меню>’,’<назв. пункта 1>’,…,’<назв. пункта n>’)
Номер выбранной кнопки является результатом функции menu. П р и м е р. Пусть необходимо построить график функции на заданном интервале от 0 до 2 pi, цветом, выбранным из меню. Напишем script-файл:
k=menu ('цвет','красный', 'зеленый','синий') color=['r' 'g' 'b']; t=0:0.1:2*pi; s=sin(t); plot(t,s,color(k))
При нажатии на одну из кнопок с названием цвета номер этой кнопки становится результатом функции menu и попадает в переменную k. Вектор-столбец color содержит атрибуты цвета для построения графика. По номеру k нужный атрибут выбирается из массива color и указывается в команде plot. В результате, выбрав нужный пункт меню, получим график функции, построенный выбранным цветом. Для организации многократного выбора и выполнения нужных действий с помощью меню можно использовать цикл while и функцию eval. Для этого команды, реализующие необходимые действия, оформляются в виде скрипт-файлов: для каждого пункта меню – свой скрипт-файл. Затем необходимо задать символьную матрицу, например D, состоящую из названий файлов, соответствующих пунктам меню (заданий). Строки символьной матрицы должны иметь одинаковую длину. Команда return обеспечивает возврат из функции или скрипт-файла в точку вызова. В данном примере можно также использовать команду break, которая предназначена для досрочного прерывания цикла. Предположим, что необходимо выполнить по выбору три задания в любом порядке:
D=[‘f1 ’ ‘f2 ’ 'f3 ' ‘return‘]; n=1; while n<4 n=menu(‘меню’, ’пункт1’, ’пункт2’, ’пункт3’, ’выход’) eval(D(n,:)) end
Каждая строка символьной матрицы D содержит имя одного из файлов, реализующих соответствующий пункт меню. В n- й строке матрицы находится название файла, выполняющего n -й пункт меню. Обращение D(n,:) позволяет извлечь из матрицы
Создание и использование m -файлов
Эффективным способом выполнения команд в ML является применение m -файлов. Текстовый файл, содержащий набор инструкций на языке системы ML, называется m -файлом. Инструкции выполняются последовательно от начала до конца файла. Существует возможность досрочного выхода из m -файла, для этого используется оператор return. При необходимости прервать работу с ML используется оператор exit. Как уже говорилось, m -файлы бывают двух видов: script m- файл и function m- файл. Script-файлы
Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m -файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Такие файлы используются для автоматизации выполнения большого набора инструкций. В одной строке программы можно размещать несколько операторов, тогда они разделяются либо запятой, либо точкой с запятой. Если оператор длинный и не умещается на одной строке, то в конце строки ставятся три точки и дальше на другой строке продолжается набор этого оператора.
Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Перед запуском программы на выполнение необходимо установить свой каталог в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна. Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения. Создадимscript-файл, в который поместим текст программы, позволяющей вычислить длину окружности по величине ее радиуса. В текстовом редакторе наберем следующий текст:
% Вычисление длины окружности r=input (‘Введите радиус окружности ’) l=2*pi*r; disp(‘Длина окружности равна’) disp(l)
Сохраним его на диске с именем dl_okr в своей папке. Затем вызовем его для выполнения, указав в окне Command Window в командной строке имя файла dl_okr.
>> dl_okr Получим на экране: Введите радиус окружности 12 r = Длина окружности равна 75.3982 Файлы-функции
Система ML позволяет описать свои пользовательские функции и обращаться к ним, как к встроенным. В отличие от script -файла файл-функция имеет входные параметры и может передавать результат в виде выходных параметров. Файлы-функции часто применяют при решении задач вычислительной математики. Можно создавать файл-функцию с любым количеством входных и выходных параметров. Файл-функция всегда состоит из заголовка и тела функции. Заголовок функции:
function[<список вых. параметров>]=<имя функции>(<список
Заголовок функции включает ключевое слово function, имя функции, входные и выходные параметры. После заголовка записываются операторы, реализующие алгоритм поставленной задачи. Они составляют тело функции. Если функция содержит только один выходной параметр, то квадратные скобки не нужны, а если несколько, то они указываются через запятую в квадратных скобках, образуя вектор. Переменным из списка выходных параметров присваиваются значения, вычисленные в функции. Список входных параметров указывается через запятую в круглых скобках после имени функции. Имя При вызове файла-функции нужно указать ее имя и список фактических параметров. Это можно осуществить либо в командном режиме, либо из других файлов-программ или файлов-функций. Вызов (активизация) файла-функции c одним выходным параметром может иметь вид
<имя функции>(<список входных фактических параметров>)
и может использоваться в операторах присваивания или в выражении:
<имя переменной>=<имя функции>(<список входных фактических параметров>)
Выходных параметров может быть столько, сколько необходимо, тогда их список перечисляется через запятую в квадратных скобках:
function[<z1, z2,…,zn>]=<имя функции>(< список входных параметров >) < операторы, в результате которых выходные параметры получают значения>
Вызвать такую функцию можно так:
[y1, y2,…,yn]=<имя функции>(<список вх. факт. параметров>) Все переменные, используемые внутри файла-функции, а также входные и выходные параметры являются локальными. Они доступны только внутри функции. Напишемфайл-функцию, позволяющую вычислить факториал любого числа. Не будем использовать оператор цикла, а используем функцию prod(1:n). В редакторе наберем следующий текст:
% нахождение факториала любого числа function f=factorial(x) f=prod(1:x);
Сохраним файл на диске с именем factorial. Этот файл получит расширение .m. Обратимся к функции для вычисления факториала числа 5:
>> factorial(5) ans = или >> f=factorial(5) f = Отличия файла-функции от script-файла: 1. Файл-функция имеет входные и выходные параметры, а script- файл – нет. 2. Все переменные, используемые внутри файла-функции, локальны. Файл-программа работает с переменными рабочего пространства, т.е. в script- файле можно использовать глобальные данные. 3. Функция перед выполнением компилируется. Script- файл не компилируется целиком, а выполняется в режиме интерпретации. 4. Имя файла, в котором записана функция, должно совпадать с именем функции, а имя script- файла может быть любым. Программа будет выполняться быстрее, если вместо script- файла использовать файл - функцию(в случае, если это возможно).
Использование файлов-функций Файлы-функции широко используются в ML. Пользователь может с их помощью описывать свои функции для многократного выполнения, также с их помощью могут решаться следующие задачи: 1) построение графика функций; 2) численное интегрирование; 3) нахождение корней трансцендентного уравнения; 4) поиск экстремумов функции; 5) решение систем дифференциальных уравнений. Построение графика
График функции на заданном отрезке, символьное выражение (формула) которой записано в файле-функции, можно построить, используя команду
fplot (fun, interval),
где fun – имя функции или символьное выражение, задающее формулу вычисления; interval – отрезок, который задается вектором из двух значений: начального и конечного значения отрезка. В качестве примера построим график функции х 2 -1 на отрезке от 0 до p. Для функции х 2 -1 напишем файл-функцию. В текстовом редакторе наберем следующий текст:
function f=func(x) f=x.^2-1;
Сохраним его в файле с именем func.m. Для построения графика (рис. 30) выполним команду
>> fplot('func',[0 pi])
Или используем вместо имени функции символьное выражение
>> fplot('sin(x)',[0 pi])
Рис. 30
Вычисление интеграла
Самым простым численным методом нахождения определенных интегралов является метод трапеций, который реализован функцией trapz (x, y),где x и y – векторы, задающие значения аргумента и функции в пределах интегрирования. Для ее использования не требуется оформление подынтегральной функции в качестве файла-функции. Вычислим интеграл >> x=0:pi/100:pi; >> y=sin(x); >> z=trapz(x,y); z = 1.9998
Получили приближенное значение интеграла. Увеличив шаг интегрирования до pi/1000, получим более точное значение – 2. Более точные методы реализованы в функциях quad, quad8, quadl. Функция quad основана на квадратурной формуле Симпсона, а функция quadl предназначена для вычисления интеграла по более точным формулам Гаусса–Лейбница. Функция quad8 реализует метод Ньютона–Котеса восьмого порядка. Все три функции имеют одинаковый набор параметров:
[i, n]=quad(fun, a, b, tol, trace),
где fun – имя файла-функции или символьное выражение, определяющее подынтегральную функцию (оно должно быть заключено в апострофы); a, b – пределы интегрирования; tol – погрешность вычислений; trace – признак; если его значение равно единице, то при выполнении функции строится график подынтегральной функции (рис. 31), если нулю, то не строится. Последние два >> [i, n]=quad8('func', 0, pi, 1e-8, 1) i = 7.1938 n =
Рис. 31 При использовании этих численных методов задаётся тре- Функция может быть задана символьным выражением:
>> [i,n]=quad8('sin(x)', 0, pi, 1e-8, 0) i = 2.0000 n =
Такой же результат получим, если не укажем два необязательных параметра:
>> [i, n]=quad8('sin(x)', 0, pi) i = 2.0000 n =
Тот же интеграл можно вычислить с использованием функции quadl:
>> [i, n]=quadl('sin(x)',0,pi,1e-8,0) i = 2.0000 n =
Для достижения одной и той же точности понадобилось различное количество вычислений. Можно при вызове функции не указывать выходной параметр n. Тогда команда обращения к функции будет такой:
>> i=quadl('sin(x)', 0, pi, 1e-8, 0) i = 2.0000
В этом случае не используется количество значений функции, которое потребовалось вычислить для нахождения значения интеграла.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.243 (0.013 с.) |

 При выполнении этого скрипт-файла функция menu выводит на экран окно, изображенное на рис. 29.
При выполнении этого скрипт-файла функция menu выводит на экран окно, изображенное на рис. 29.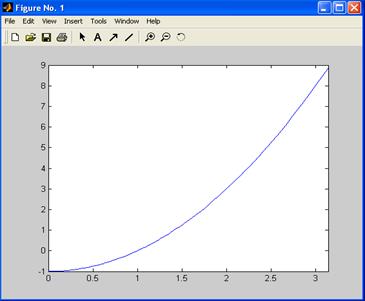
 :
:



