
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовые свойства света. ФотоэффектСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА (национальный исследовательский университет)"
КВАНТОВАЯ МЕХАНИКА АТОМНАЯ ФИЗИКА И СПЕКТРОСКОПИЯ ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ
Задачи для аудиторной и самостоятельной работы
Самара 2012 УДК 535.853 Составители: Е.А.Китаева, В.Г. Макарян, И.Л. Стукалина
Квантовая механика. Атомная физика и спектроскопия. Элементы ядерной физики: Задачи для аудиторной и самостоятельной работы / Самарский гос. аэрокосм. ун-т. Сост. Е.А.Китаева, В.Г. Макарян, И.Л. Стукалина; Самара, 2012. 32 с.
Пособие содержит вопросы для самоконтроля, принятые обозначения и основные формулы. Методические указания составлены в соответствии с программой по физике для студентов дневного отделения радиотехнического факультета. Подготовлено на кафедре физики.
Печатается по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П. Королёва.
Рецензент: к.т.н., доцент А.И. Колпаков
Тепловое излучение Вопросы: 1 Энергетическая светимость. 2 Испускательная и поглощательная способность тел. 3 Абсолютно чёрное тело. 4 Закон Кирхгофа. 5 Закон Стефана-Больцмана. 6 Закон смещения Вина. 7 Распределение энергии в спектре абсолютно чёрного тела. 8 Формула Рэлея-Джинса. 9 Квантовая гипотеза и формула Планка.
Принятые обозначения: · ω – циклическая частота. · Т – термодинамическая температура. · R · · · u · · σ – постоянная Стефана-Больцмана. · · k – постоянная Больцмана. · ħ, h – постоянная Планка. · с – скорость света. · ε – степень черноты серого тела.
Основные формулы: · Закон Кирхгофа:
где · Зависимость максимальной спектральной плотности энергетической светимости от температуры:
где · Закон Стефана-Больцмана:
· Энергетическая светимость серого тела:
где · Закон смещения Вина:
где · Формула Рэлея-Джинса:
где k – постоянная Больцмана · Формула Планка:
· Объемная плотность энергии:
· Связь универсальной функции Кирхгофа со спектральной плотностью энергии:
Задачи 1 Температура абсолютно черного тела изменилась при нагревании от 1000 К до 3000 К. Во сколько раз увеличилась при этом его энергетическая светимость? На сколько изменилась длина волны, на которую приходится максимум спектральной плотности энергетической светимости? Во сколько раз увеличилась его максимальная спектральная плотность энергетической светимости? 2 Абсолютно черное тело имеет температуру 3 Радиус вольфрамовой нити в электрической лампочке равен 0,2 мм, длина равна 5 см. При включении лампочки в цепь с напряжением 220 В через лампочку течет ток силой 0,27 А. Найти температуру нити лампочки. Считать, что в состоянии равновесия все выделяющееся в нити тепло теряется в результате лучеиспускания. Коэффициент черноты для вольфрама при этой температуре равен 0,31. 4 Энергетическая светимость абсолютно черного тела равна 3 Вт/см 2. Определить длину волны, отвечающую максимуму испускательной способности этого тела. 5 Излучение солнца по спектральному составу близко к излучению абсолютно черного тела, для которого длина волны, соответствующая максимуму спектральной плотности энергетической светимости равна 0,48 мкм. Найти массу, теряемую солнцем ежесекундно за счет излучения. Оценить время, за которое масса солнца уменьшится на 1%. 6 Два абсолютно черных тела имеют одинаковую температуру 1000 К. Площадь поверхности одного тела в два раза меньше площади поверхности второго тела. Первое тело охлаждают на 500 К. На сколько нужно нагреть второе тело, чтобы общая энергетическая светимость тел не изменилась? 7 Медный шарик радиусом 0,6 см поместили в откачанный сосуд, температура стенок которого поддерживается близкой к абсолютному нулю. Начальная температура шарика 300 К. Считая поверхность шарика абсолютно черной, найти, через сколько времени его температура уменьшится в 2 раза. 8 Поверхность тела нагрета до температуры 1000 К. Затем одна половина этой поверхности нагревается на 100 К, а другая охлаждается на 100 К. Во сколько раз изменится энергетическая светимость поверхности этого тела? 9 Какую мощность надо подводить к зачерненному металлическому шарику радиусом 2 см, чтобы поддерживать его температуру на 27 К выше температуры окружающей среды? Температура окружающей среды равна 293 К. Считать, что тепло теряется только вследствие излучения. 10 Температура абсолютно черного тела равна 2 кК. Определить: а) спектральную плотность энергии для длины волны λ=600 нм; б) объемную плотность энергии в интервале длин волн от λ1=590 нм до λ1=610 нм. Принять, что средняя спектральная плотность энергии тела в этом интервале равна значению, найденному для длины волны λ=600 нм. 11 Исследование спектра излучения солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны λ=500 нм. Принимая солнце за абсолютно черное тело, определить: а) энергетическую светимость солнца; б) поток энергии, излучаемый солнцем; в) массу электромагнитных волн (всех длин), излучаемых солнцем за 1 с. 12 Муфельная печь потребляет мощность Р = 1 кВт. Температура ее внутренней поверхности при открытом отверстии площадью S = 25 см 2 равна 1,2 кК. Считая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками.
Ответы
1. 81; 1,93 мкм; в 243 раза. 2. 290 К. 3. 2700 К. 4. 3,4 мкм. 5. Задачи
1 При поочередном освещении поверхности некоторого металла светом с длиной волны 0,35 мкм и 0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в два раза. Найти работу выхода с поверхности этого металла. 2 Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра: а) ультрафиолетовым излучением с длиной волны 3 Определить красную границу λο фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны λ=400 нм максимальная скорость фотоэлектронов равна 0,65 Мм/с. 4 Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов 5 Определить максимальную скорость фотоэлектронов, вылетающих из металла при облучении 6 Максимальная длина волны света, вызывающего фотоэффект с поверхности пластины равна 0,5 мкм. Если на эту пластину подать задерживающий потенциал, равный 2 В, то при какой минимальной частоте начнётся фотоэффект? 7 Лазер мощностью 1 мВт генерирует монохроматическое излучение с длиной волны равной 0,6 мкм. За какое время лазер испускает фотоны, суммарная масса которых равна массе покоя протона ( 8 Сетчатка глаза начинает реагировать на жёлтый свет с длиной волны 600 нм при мощности падающего на него излучения 9 Найти массу фотона, импульс которого равен импульсу молекулы водорода при температуре t = 20 ° С. Скорость молекулы считать равной средней квадратичной скорости. 10 Найти частоту ν света, вырывающего из металла электроны, которые полностью задерживаются разностью потенциалов 3 В. Фотоэффект прекращается при частоте света 11 Фотон с λ=0,170 12 При некотором максимальном значении задерживающей разности потенциалов фототок с поверхности лития (
Ответы
1. 1,9 эВ. 2.
Задачи
1 Стенка колбы у электролампы накаливания представляет собой посеребренную сферу радиусом 4 см. Лампа потребляет мощность 50 Вт, 90% которых затрачивается на излучение. Во сколько раз давление газа в колбе, равное 1,5 мкПа, меньше светового давления? 2 Небольшое идеально отражающее зеркальце массы 10 мг подвешено на невесомой нити длины 10 см. Найти угол, на который отклонится нить, если по нормали к зеркальцу в горизонтальном направлении произвести выстрел коротким импульсом лазерного излучения с энергией 13 Дж? 3 Пучок монохроматического света с длиной волны 663 нм падает нормально на зеркальную плоскую поверхность. Поток энергии имеет мощность 0,6 Вт. Определить силу давления, испытываемую этой поверхностью, а также число фотонов, падающих на нее за время 5 с. 4 Параллельный пучок света длиной волны λ=500 нм падает нормально на зачерненную поверхность, производя давление p = 10 мкПа. Определить: а) концентрацию фотонов в пучке; б) число фотонов, падающих на поверхность площадью 1 м 2 за время 1 с. 5 Русский астроном Ф.А. Бредихин объяснил форму кометных хвостов световым давлением солнечных лучей. Найти световое давление солнечных лучей на абсолютно черное тело, помещенное на таком же расстоянии от Солнца, как и Земля. Какую массу должна иметь частица в кометном хвосте, помещенная на этом расстоянии, чтобы сила светового давления на нее уравновешивалась силой притяжения частицы Солнцем? Площадь частицы, отражающую все падающие на нее лучи, считать равной S =0,5·10-12 м 2. Солнечная постоянная K = 1,37 кВт/м 2. 6 Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. При этом длина волны излучения, рассеянного под углами 60 и 120 градусов отличаются друг от друга в два раза. Считая, что рассеяние происходит на свободных электронах, найти длину волны падающего излучения. 7 Фотон с энергией 1 МэВ рассеялся на свободном покоившемся электроне. Найти кинетическую энергию электрона отдачи, если в результате рассеяния длина волны фотона изменилась на 25%. 8 В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол θ=90°. Энергия рассеянного фотона равна 0,4 МэВ. Определить энергию фотона до рассеяния. 9 Фотон с энергией 0,75 МэВ рассеялся на свободном электроне под углом θ=60°. Принимая, что кинетическая энергия и импульс электрона до соударения с фотоном были пренебрежимо малы, определить: а) энергию рассеянного фотона; б) кинетическую энергию электрона отдачи; в) направление его движения. 10 При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния
Ответы
1. 10. 2.
Задачи
1 Найти длину волны де Бройля для: а) электрона, движущегося со скоростью 2 α-частица движется по окружности радиусом r = 8,3 мм в однородном магнитном поле, напряженность которого Н = 18,9 кА/м. Найти длину волны де Бройля для α-частицы. 3 4 Какую энергию необходимо дополнительно сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 пм до 50 пм. 5 Параллельный пучок моноэнергетических электронов падает на диафрагму с узкой прямоугольной щелью ширины 1,0 мкм. Определить скорость этих электронов, если на экране, отстающем от щели на расстояние 50 см, ширина центрального дифракционного максимума 0,36 мм. 6 Пучок электронов с кинетической энергией 10 кэВ проходит через тонкую поликристаллическую фольгу и образует систему дифракционных колец на экране, отстоящем от фольги на 10 см. Найти межплоскостное расстояние, для которого максимум отражения третьего порядка соответствует кольцу с радиусом 1,6 см. 7 Частица массы 8 Оценить наименьшие ошибки, с которыми можно определить скорость электрона, протона и шарика массы 1 мг, если координаты частиц и центра шарика установлены с неопределенностью 1 мкм. 9 Показать, что для частицы, неопределенность местоположения которой 10 Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы 11 Частица массы
Ответы
1. 730 10-12 м; 145 10-12 м; 6,6 10-29 м. 2. 10,5 пм. 3. увеличится в 2 раза. 4. 0,45 кэВ. 5. 2 Мм/с. 6. 2,3 Задачи
1 Проверить следующее операторное равенство: 2 Найти результат действия операторов 3 Найти собственное значение оператора 4 Найти собственные функции 5 Проверить следующие правила коммутации: 6 С помощью правил коммутации, приведенных в предыдущей задаче, показать, что: Ответы
2. Уравнение Шредингера
Вопросы: 1 Временное уравнение Шредингера. 2 Стационарное уравнение Шредингера 3 Уравнение Шредингера в операторной форме 4 Стандартные условия, накладываемые на волновую функцию.
Принятые обозначения: · · · · · · · · ·
Основные формулы: · Временное уравнение Шредингера:
· Стационарное уравнение Шредингера:
если потенциал · Вероятность обнаружить частицу в интервале от x1 до x2:
· Оператор Лапласа в сферических координатах для функции
· Коэффициент прозрачности прямоугольного потенциального барьера конечной ширины:
где
Задачи
1 Написать уравнение Шредингера для: а) электрона, находящегося в водородоподобном атоме; б) линейного гармонического осциллятора. 2 Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины 3 Электрон наводится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы такова, что энергетические уровни расположены весьма густо. Найти плотность уровней 4 Электрон находится в одномерном потенциальном ящике шириной 5 6 Волновая функция частицы массы 7 Определить энергию электрона атома водорода в стационарном состоянии, для которого волновая функция 8 Волновая функция электрона в основном состоянии атома водорода имеет вид 9
Ответы
2.
Задачи
1 Сколько спектральных линий будет испускать атомарный водород, который возбуждают на 2 Найти наименьшую 3 Какие линии содержит спектр поглощения атомарного водорода в диапазоне длин волн от 94,5 до 130 нм? 4 Какую наименьшую энергию 5 В каких пределах должны лежать длины волн l монохроматического света, чтобы при возбуждении атома водорода квантами этого света наблюдались три спектральные линии? 6 На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Постоянная решетки 7 Вычислить постоянную Ридберга, если известно, что для ионов 8 Найти длину волны головной линии той спектральной серии ионов 9 Энергия связи электрона в основном состоянии атома гелия равна 10 Покоившийся атом водорода испустил фотон, соответствующий головной линии серии Лаймана. Какую скорость приобрел атом? 11 Покоящийся ион
Ответы 1.
Свойства атомов
Вопросы: 1 Принцип Паули. 2 Связь периодичности структуры электронных оболочек атомов с периодической таблицей элементов Менделеева. 3 Электронные слои атомов и их обозначения. 4 Термы атомов и их обозначения. 5 Квантовые числа: главное, орбитальное, магнитное, спиновое и полного момента. 6 Механические моменты атома. 7 Правила отбора при излучении атомов. 8 Правила Хунда.
Принятые обозначения: · · · · · ·
Основные формулы: · Спектральные обозначения термов: где · Орбитальный механический момент атома:
· Спиновой механический момент атома:
· Полный механический момент атома:
· Мультиплетность: · Правила отбора для квантовых чисел · · Правила Хунда: а) наименьшей энергией обладает терм с максимальным значением спинового квантового числа б) орбитальное квантовое число в) внутреннее квантовое число
Задачи
1 Выписать спектральные о6означения термов атома водорода, электрон которого наводится в состоянии с главным квантовым числом n =3. 2 Найти возможные значения полных механических моментов атомов, находящихся в состояниях: а) 3 Выписать спектральные символы термов двухэлектронной системы
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.143 (0.022 с.) |


 − энергетическая светимость.
− энергетическая светимость. − испускательная способность тела (спектральная плотность энергетической светимости).
− испускательная способность тела (спектральная плотность энергетической светимости). − поглощающая способность тела.
− поглощающая способность тела.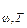 − спектральная плотность энергии теплового излучения.
− спектральная плотность энергии теплового излучения. − объёмная плотность энергии теплового излучения.
− объёмная плотность энергии теплового излучения. – постоянная Вина.
– постоянная Вина. ,
, – универсальная функция Кирхгофа (испускательная способность абсолютно чёрного тела).
– универсальная функция Кирхгофа (испускательная способность абсолютно чёрного тела). ,
,
 .
. ,
, – степень черноты серого тела.
– степень черноты серого тела.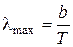 ,
, – это длина волны, на которую приходится максимальная энергия излучения.
– это длина волны, на которую приходится максимальная энергия излучения. ,
, ,
,  .
. .
.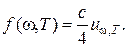
 =2900 К. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на 9 мкм. До какой температуры
=2900 К. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на 9 мкм. До какой температуры 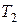 охладилось тело?
охладилось тело? ;
;  . 6. 100 К. 7. 3 часа. 8. 1,06. 9. 3 Вт. 10. 30 109 Вт/м 3. 11. 64 МВт/м 2; 3,9 1026 Вт; 4,3 109 кг. 12. 0,71.
. 6. 100 К. 7. 3 часа. 8. 1,06. 9. 3 Вт. 10. 30 109 Вт/м 3. 11. 64 МВт/м 2; 3,9 1026 Вт; 4,3 109 кг. 12. 0,71.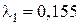 мкм; б)
мкм; б)  -излучением с длиной волны
-излучением с длиной волны  пм, если работа выхода электронов из серебра равна 4,7 эВ.
пм, если работа выхода электронов из серебра равна 4,7 эВ. =3,7 В. Если платиновую пластинку с работой выхода
=3,7 В. Если платиновую пластинку с работой выхода  эВ заменить другой пластинкой, то задерживающую разность потенциалов придется увеличить до 6 В. Определить работу выхода
эВ заменить другой пластинкой, то задерживающую разность потенциалов придется увеличить до 6 В. Определить работу выхода  электронов с поверхности этой пластинки.
электронов с поверхности этой пластинки. )?
)? Вт. Сколько фотонов при этом падает на сетчатку каждую секунду?
Вт. Сколько фотонов при этом падает на сетчатку каждую секунду? Гц. Найти работу выхода электрона из металла.
Гц. Найти работу выхода электрона из металла. вырывает из покоившегося атома электрон, энергия связи которого Е = 69,3 кэВ. Найти импульс, переданный атому в результате этого процесса, если электрон вылетел под прямым углом к направлению падающего фотона.
вырывает из покоившегося атома электрон, энергия связи которого Е = 69,3 кэВ. Найти импульс, переданный атому в результате этого процесса, если электрон вылетел под прямым углом к направлению падающего фотона. ), освещаемого светом с длиной волны λo, прекращается. Изменив длину волны света в n =1,5 раза, установили, что для прекращения тока необходимо увеличить задерживающую разность потенциалов в
), освещаемого светом с длиной волны λo, прекращается. Изменив длину волны света в n =1,5 раза, установили, что для прекращения тока необходимо увеличить задерживающую разность потенциалов в  2,0 раза. Вычислить λο.
2,0 раза. Вычислить λο. м/с;
м/с;  м/с. 3. 651 нм. 4. 4 эВ. 5.
м/с. 3. 651 нм. 4. 4 эВ. 5.  м/с. 6.
м/с. 6.  Гц. 7.
Гц. 7.  с. 8.
с. 8.  . 9.
. 9.  кг. 10.
кг. 10.  Гц. 11.
Гц. 11.  кг м/с. 12.
кг м/с. 12. 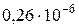 м.
м. . Найти энергию и импульс рассеянного фотона.
. Найти энергию и импульс рассеянного фотона. . 3.
. 3.  ;
;  . 4.
. 4.  ;
;  . 5.
. 5.  ;
;  . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  9.
9.  ;
;  ;
;  . 10.
. 10. 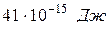 ;
;  .
. м/с; б) атома водорода, движущегося со средней квадратичной скоростью при температуре 300 К; в) шарика массой 1 г, движущегося со скоростью V = 1 см/с.
м/с; б) атома водорода, движущегося со средней квадратичной скоростью при температуре 300 К; в) шарика массой 1 г, движущегося со скоростью V = 1 см/с. Частица движется слева направо в одномерном потенциальном поле, показанном на рисунке 1. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы Т = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер.
Частица движется слева направо в одномерном потенциальном поле, показанном на рисунке 1. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы Т = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер.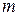 находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы
находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы  . Найти возможные значения энергии частицы, имея в виду, что реализуются лишь такие состояния ее движения, для которых в пределах данной ямы укладывается целое число дебройлевских полуволн.
. Найти возможные значения энергии частицы, имея в виду, что реализуются лишь такие состояния ее движения, для которых в пределах данной ямы укладывается целое число дебройлевских полуволн. , где
, где  − ее дебройлевская длина волны, неопределенность скорости равна по порядку величины самой скорости частицы.
− ее дебройлевская длина волны, неопределенность скорости равна по порядку величины самой скорости частицы. (гармонический осциллятор). Оценить с помощью соотношения неопределенностей минимально возможную энергию частицы в таком поле.
(гармонический осциллятор). Оценить с помощью соотношения неопределенностей минимально возможную энергию частицы в таком поле. . 7.
. 7.  . 8. 100 м/с; 0,1 м/с; 10-22 м/с. 9.
. 8. 100 м/с; 0,1 м/с; 10-22 м/с. 9.  . 10.
. 10.  . 11.
. 11.  .
. .
.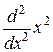 и
и 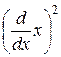 на функции: a)
на функции: a) 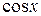 и б)
и б) 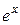 .
.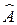
 , если:
, если: 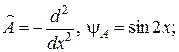


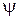 и собственные значения следующих операторов:
и собственные значения следующих операторов: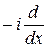 , если
, если 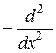 , если
, если 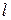 .
.


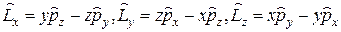 и
и 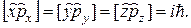
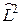 коммутирует с операторами
коммутирует с операторами 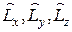
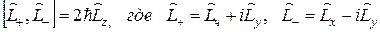 .
.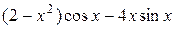 ;
;  ;
;  ;
; 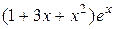 . 3. 4; 1;
. 3. 4; 1;  . 4.
. 4. 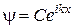 , где
, где 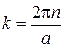 ,
, 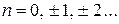 ;
; 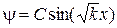 , где
, где  ,
, 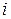 – мнимая единица,
– мнимая единица, 
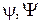 − волновая функция, описывающая состояние частицы.
− волновая функция, описывающая состояние частицы. – полная энергия частицы.
– полная энергия частицы.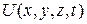 – потенциальная функция координат и времени.
– потенциальная функция координат и времени.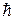 − постоянная Планка.
− постоянная Планка. − оператор Лапласа.
− оператор Лапласа. – вероятность.
– вероятность. – коэффициент прозрачности.
– коэффициент прозрачности.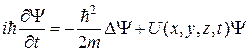 .
.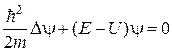 ,
,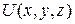 не зависит от времени.
не зависит от времени.

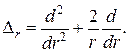
 ,
,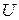 – высота потенциального барьера,
– высота потенциального барьера, 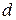 − ширина барьера.
− ширина барьера.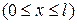 . Найти вероятность пребывания частицы в области
. Найти вероятность пребывания частицы в области 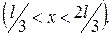 .
.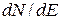 , т.е. их число на единичный интервал энергии, в зависимости от
, т.е. их число на единичный интервал энергии, в зависимости от 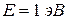 , если ширина ямы равна 1 см.
, если ширина ямы равна 1 см. электрона, если
электрона, если 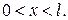
 Частица массы
Частица массы 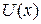 , вид которого показан на рисунке 2, где
, вид которого показан на рисунке 2, где  . Найти:
. Найти: 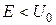 , привести это уравнение к виду:
, привести это уравнение к виду: 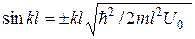 , где
, где 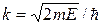 . Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы образуют дискретный спектр;
. Показать с помощью графического решения этого уравнения, что возможные значения энергии частицы образуют дискретный спектр; 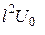 , при котором появляется первый энергетический ypoвeнь в области
, при котором появляется первый энергетический ypoвeнь в области 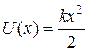 имеет вид
имеет вид  , где
, где  − нормировочный коэффициент,
− нормировочный коэффициент, 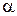 − положительная постоянная. Найти с помощью уравнения Шредингера постоянную
− положительная постоянная. Найти с помощью уравнения Шредингера постоянную 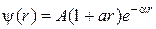 , где
, где 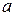 и
и 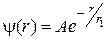 , где
, где  − первый боровский радиус. Найти:
− первый боровский радиус. Найти:  Электрон с энергией
Электрон с энергией  движется в положительном направлении оси
движется в положительном направлении оси  (смотри рисунок 3). Высота U потенциального барьера равна 5 эВ. При какой ширине d барьера вероятность
(смотри рисунок 3). Высота U потенциального барьера равна 5 эВ. При какой ширине d барьера вероятность 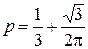 . 3. 0,8 107 уров/эВ. 4.
. 3. 0,8 107 уров/эВ. 4.  . 5. б)
. 5. б) 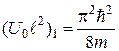 . 6.
. 6.  ;
;  7.
7.  . 8. rвф=r1;
. 8. rвф=r1; 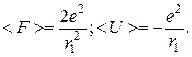 9.» 0,5 нм.
9.» 0,5 нм. -ый энергетический уровень?
-ый энергетический уровень? и наибольшую
и наибольшую  (в электронвольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серии спектра водорода? Какую наименьшую скорость
(в электронвольтах) должны иметь электроны, чтобы при возбуждении атомов водорода ударами этих электронов появились все линии всех серии спектра водорода? Какую наименьшую скорость  должны иметь эти электроны?
должны иметь эти электроны? , разность длин волн между головными линиями серии Бальмера и Лаймана составляет 133,7 нм.
, разность длин волн между головными линиями серии Бальмера и Лаймана составляет 133,7 нм.
 . Найти энергию, необходимую для удаления обоих электронов из этого атома.
. Найти энергию, необходимую для удаления обоих электронов из этого атома. где n = 1, 2, 3,… 2. 365 нм; 656 нм. 3. 121,6 нм; 102,6 нм; 97,3 нм. 4. 13,6 эВ; 2,2 Мм/с. 5. (102,3¸121,5) нм. 6. n1=2, n2=3. 7. 2,07 1016 1/ c. 8. 0,47 мкм. 9. 7,9 эВ. 10. 6 км/с. 11. 3,1 106 м/с.
где n = 1, 2, 3,… 2. 365 нм; 656 нм. 3. 121,6 нм; 102,6 нм; 97,3 нм. 4. 13,6 эВ; 2,2 Мм/с. 5. (102,3¸121,5) нм. 6. n1=2, n2=3. 7. 2,07 1016 1/ c. 8. 0,47 мкм. 9. 7,9 эВ. 10. 6 км/с. 11. 3,1 106 м/с. – орбитальное квантовое число.
– орбитальное квантовое число. – спиновое квантовое число.
– спиновое квантовое число. – внутреннее квантовое число.
– внутреннее квантовое число. − мультиплетность.
− мультиплетность. – орбитальный, спиновой и полный механический моменты.
– орбитальный, спиновой и полный механический моменты.  ,
, – буквенный символ орбитального квантового числа L=0,1,2,3,4,5,6,…(n-1), а соответствующий буквенный символ:
– буквенный символ орбитального квантового числа L=0,1,2,3,4,5,6,…(n-1), а соответствующий буквенный символ:  .
. .
. .
. .
. .
. :
: .
. должно быть наибольшим;
должно быть наибольшим; , если подоболочка заполнена не более, чем наполовину, и по формуле
, если подоболочка заполнена не более, чем наполовину, и по формуле  , если подоболочка заполнена более, чем наполовину.
, если подоболочка заполнена более, чем наполовину. и б)
и б)  .
.


