Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К.2. Фотоэффект.законы столетоваСодержание книги Поиск на нашем сайте К. 3. Закономерности в атомных спектрах. Впервые линии в спектре водорода наблюдал и подробно описал немецкий физик И. Фраунгофер. Вначале Фраунгофер обнаружил всего 4 линии, которые впоследствии стали называться линиями H α, H β, H γ, и H δ. 1885 году И. Бальмер, (Швейцария), тщательно проанализировал снимки и заметил следующее. Если ввести некоторое (как его назвал Бальмер, основное) число k, то длины волн линий H α, H β, H γ, и H δ могут быть выражены таким образом: Вскоре были обнаружены другие линии в спектре поглощения водорода (сейчас известно около 30 линий только в видимой области спектра). Ридберг записал формулу Бальмера в «перевернутом виде, где ввел постянную ридберга вместо основного числа и получил обобщенную формулу Бальмера
этой формуле для каждой серии линий число m имеет постоянное значение от 1 до 5: m =1, 2, 3, 4, 5, а внутри данной серии число n принимает ряд возрастающих численных значений, начиная от m + 1. Существуют серии: серия Бальмера (переход с верхних эн уровней на второй), серия Лаймана (с верх эн уровней на 3) и т.д… Постулаты Бора. Целью работы было объединить в единое целое следующее: эмпирические закономерности в спектре атома водорода; ядерную модель атома Резерфорда; квантовый характер испускания и поглощения света. Первоначально в теории Бора сохранялась классическое описание движения электронов, но для достижения цели ему пришлось наложить некоторые ограничения, которые он сформулировал в виде постулатов: 1 Постулат стацион. состояний: сущ-ют некоторые стацион-е состояния атома, находясь в которых атом не излучает энергии, этим стац-ым состояниям соответствуют опред-е (стац-е) орбиты, по которым движ-ся электрон. 2 Правило квантования орбит: в стац-ых состояниях атом электрона двигаясь по круговой орбите должен иметь строго опред-ое квантованные значения момента импульса, удовл-ие условию: (4) mυnrn = nħ; n=1,2,3,…-N стац-ой орбиты; r-радиус стац-ой орбиты; υ–скорость движ-ия электрона по орбите rn; 3 Правило частот: при переходе из одного стац-го состояния в другое, испускается или поглощается один квант энергии: Еn < Еm -поглощение энергии Еn-Еm = h υnm Еn > Еm –излучение энергии Постулаты 1 и 3 были подтверждены опытом Франка и Герца (1914г.):
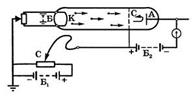
в трубке заполненной парами ртути под небольшим давлением(~1 мм рт ст), имелись три электрода: катод К, сетка С и анод А; электроны, вылетавшие из К вследствие термоэлектронной эмиссии, ускорялись разностью потенциалов U, приложенной между К и С; эту разность потенциалов можно было плавно менять с помощью потенциометра П; между С и А создавалось слабое электр-ое поле, тормозившее движ-е электронов к А. Исследовалась зависимость силы тока в цепи анода от напряжения между К и С: сила тока измерялась гальванометром Г, напряжение – вольтметром В; видно, что сила тока вначале монотонно возрастает, достигая max приU=4,9 В, после чего с дальнейшим увеличением U резко падает, достигая min, и снова начинает расти; такой ход кривой объясняется тем, что вследствие дискретности энергетич-х уровней атомы могут воспринимать энергию только порциями: ∆Е1=Е2-Е1 либо ∆Е2=Е3-Е1 и т.д., где Е1,Е2,Е3…-энергия 1-го, 2-го, 3-го и т.д. стац-ых состояний. Таким образом, в опытах непосредственно обнаруживается сущ-ие у атомов дискретных энергетических уровней могут воспринимать энергию только порциями:
Уравнение Шредингера. Уравн-е Шред-ра – основное уравнение квантовой механики. Квант-я механика – теория устанавливающая способописания и законы движ-я микрочастицы и их систем, а также связь величин характериз-х микроч-цу системы с физич-ми велич-ми, непосредственно измеренные на опыте. наличие волновых свойств микрочастицы не позволяет использовать ур-ие (1). Ур-ие движ-ия микрочастицы было предложено Шред-ом в 1926г. ψ = ψ(x,y,z,t)-(ВФ)→ уравнение движ-ия микрочастицы должно быть относительно этой функции → уравнение должно быть волновым, т.к. с его помощью мы должны объяснить эксперименты по дифракции микрочастицы.
Временное урвнение Шредингера: (2) – основное уравн-е нерелятивистской квантовой механики, т.е справедливо для любой частицы движ-ся со скоростью << скорости света.
Уравнение Шр-ра добавляется важными условиями, накладывающимися на ВФ: 1.ВФ должна быть конечна, однозначна и непрерывна. 2. Первые производные должны быть непрерывны. 3. функция должна быть квадратично интегрируема: -∞∫∞|Ψ|2 dV = const=1 Во многих случаях потенциальная энергия частицы зависит только от координаты, т.е. U=U(x,y,z). В этом случае можно получить стационарное уравнение Шредингера, в котором исключена зависимость ВФ от времени t.
Принцип Паули. Распределение электронов по состояниям, управляется принципом Паули(ПП) установленном на обобщении экспериментальных рез-ов. ПП утверждает, что в каждом состоянии характериз-ся 4 квант-ми числами (n-главное квант.(n=1,2,3); l-орбитальное (l=0,1,2…n-1); ml – магнитное (ml = -l…,-1,0,1,…+l); ms- магнитное спиновое (ms =+1/2, -1/2)) может нах-ся не >> 1 электрона. В соответствии с ПП каждый вновь присоед-ый электрон будет занимать состояния с большей энергией. Совокупность электронов нах-ся во всех возможных состояниях с одинаковой знач-ем n(главное квант-е число) будем наз-ть электронным слоем или оболочкой. (K,L,M). Заполненный слой – слой, в котором все входящие в него состояния в атоме реализованы. Ядерные силы. Нуклоны связаны между собой особыми силами притяжения – ядерными силами. Основные свойства: 1. fяд >> fкул, fграв. 2.они короткодействующие, т.е. действуют на расстояниях ~ 10-15 м = 1 Ф. 3. они явл-ся силами особого рода, их природа и свойства изучены недостаточно. Модели атомного ядра. 1. Капельная модель(первая): в основе модели лежит аналогия между свойствами ядра и капли жидкости. Общее: а) силы, действующие между молекулами жидкости, имеют малый радиус действия. б) ядерные частицы, также как и молекулы жидкости, обладают достаточной подвижностью. Доказательством этого служит установление у p и n значительных моментов импульсов. в) плотность вещества в жидком состоянии при данной темпер-ре и давлении постоянна и не зависит от числа молекул, а ядро имеет постоянну удельную энергию связи, и плотность, не зависящую от числа нуклонов в ядре. Отличие: ядро-капля заряжено и подчиняется законам квантовой механики. Капельная модель хорошо поясняет многие свойства ятомных ядер. С ее помощью установлен критерий устоячивости атомных ядер: Рассмотр ядра с А=const Z =А/(1,98+0,015А2/3) → Z = А/2 (Nр ≈ Nn) – для легких ядер. 2. оболочечная модель(аналогия со строением электр оболочки атома) Согласно ОМ нуклоны дв-ся независимо в поле, создав-ом самими нукл-ми. Из ОМ след.: 1.нуклоны в ядре обр-т определенные электронные оболочки и подоболочки. 2.существ 2е сист-мы нуклонных сост-ий: протонная и нейтронная(заполн не завис др от др)3.Ядра имеющие только заполненые нукл-е оболочки обладают повышенной устойчивостью и большей распространненостью. Рассчеты по оболочечной модели показали, что наиболее устойчивыми пол-ми оказались с числом p или n: 2,8,20,28,50,82,126,152 (магические числа). Дважды магические элементы(и n и p):24He, 816O, 2040Ca,82208Pb.
К.8. Радиоактивность. Природа α, β, γ распадов. Закон радиоакт-го распада. Период полураспада. Активность радиоакт-го вещества. р/акт - испускание ядрами некот-х элем-ов различных частиц сопровождающийся переходом ядра в др. состояние и изменение его параметра. У достаточно тяжелых элементов(после 82Pb) ядерные силы уже не обеспечивают устойчивости ядра. Такие ядра могут самопроизвольно распадаться, превращаясь в ядра более легких элементов. Это явление наз-ся р/акт распадом. Распад атомных ядер сопровожд-ся испусканием различных видов з/акт излучений и некоторых элементов частиц. 1896г –Анри Беккерель обнаружил, что соли урана испускают невидимые лучи со сле-ми свойствами: 1.способны вызывать люминисценцию 2.проникать сквозь слои непрозрачных веществ. 3.ионизируют газы. 4.обладают фотографич-им действием. Дальнейшее исследование было проделано Марией и Пьером Кюри, Э.Резерфордом. Ими были установлено, что естественная р/акт свойственна не только урану, но и многим тяжелым элементам: 89Ас, 90Тh, 84210Ро, 88Ra. Все эти элементы были названы р/акт, а испускаемые ими лучи-р/акт-ым излучением. Радиоактивное излучение явл-ся сложным и состоит из трех видов излучения. Анализ его состава был сделан Кюри по отклонению в магн-ом поле. Характер отклонения лучей в магн-ом поле показывает, что α-лучи несут полож-ый, β-лучи отриц-ый заряд, γ-лучи не заряжены. α-лучи – поток ядер гелея (24Не → Zα = +2e). пролетая сквозь вещество α-частица ионизирует его атомы действуя на них своим электр-им полем. Израсходовав свою энергию, α-частица останавл-ся, захватывает электрон из вещ-ва и превращается в нейтральный атом гелия. Пробег (проникающая способность)-путь, проходимый р/акт излучателем в вещ-ве. Ионизирующая способность - число пар ионов, создаваемых излучением на пробеге. β-лучи – поток быстрых электронов(υβ~108м/с). β-частицы обладают меньшей иониз-ей спос-тью, но большим пробегом, чем α-частицы. Энергия β-частиц идет на: ионизацию; возбуждение вторичного рентген-го излучения, источником которого явл-ся оболочка атома. Γ-лучи – эл/магн волна(λγ ~ 10-12м). источником γ-излучения явл-ся атомное ядро. Энергия идет на: фотоэффект, эффект Комптона; образование электронно-позитронных пар εγ ≥ 1,02 МэВ – ядро распадается на отриц-ый электрон и полож-ый.
Закон р/акт распада. Радиоакт.распад- естеств-е радиоакт-е превращ-е ядер, происходящее самопроизвольно. р/акт распад ведет к постепенному уменьшению числа атомов р/акт излучения. Пусть dN-число атомов, распадающихся за время dt: dN =-λNdt (1), где λ-постоянная распада (минус указывает на уменьшение числа атомов). dN/N характе-ет относительное уменьшение dt атомных ядер в единицу времени. dN/N = - λdt → ln N = -λt + ln с (2), ln c-определ-ся из нач-ых условий: t=0 → N=N0/ N = N0 e-λt (3) – закон р/акт распада. N0-число атомов р/акт элемента в нач-ый момент времени, N-число атомов этого же элемента, оставшихся к моменту времени t. Для характер-ки быстроты рапада вводят понятие периода полураспада (время, в течение которого распадается половина атомов ядер р/акт вещ-ва). Т = ln 2/λ = 0,693/λ Время жизни р/акт атома – величина обратно пропорц-ая постоянной распада: τ = 1/λ = Тln2 =1,44 Т Активность р/акт распада – число атомных распадов, совершающихся в р/акт элементе за един-цу времени: а = |dNdt| = λ N. Продукт р/акт распада сам может бать р/акт и проходить несколько промежуточных стадий, образуя цепочку р/акт элементов, заканчивающуюся стабильным элементом. Такая цепочка элементов наз-ся семейством: 1-ое семейство урана: 2-ое сем-во нептуния: 3-е сем-во актиноурана: 4-ое сем-во тория: К. 10. Твердые тела. Любое твердое тело представляет собой систему многих микрочастиц. Существует два способа описания систем многих частиц: термодинамическое и статистическое описание. При термод-ом описании систему рассматривают как макроскопич-ую систему, не интересуясь частицами. Такая система характериз-ся макропараметрами: р, Т, V. Этот способ не дает возможности исследовать свойства системы, которые зависят от микроструктуры вещества (проводимость). Статистич-ий метод позволяет найти наиболее вероятные распределения частиц системы по координатам, импульсам, энергиям. Математически задача стат-го метода сводится к описанию функции распределения частиц(ФР). ФР характер-ет плотность вероятности распределения частиц системы по фазовому пространству координат и импульсов (для классич-х частиц) и по квантовым состояниям (для кван-х частиц). Характер ФР зависит от индивидуальных свойств частиц системы. Идеальный газ подчиняется распределению Максвелла-Больцмана, а электронный газ – распределению Ферми-Дирака. Донорная примесь От латинского «donare» — давать, жертвовать.Рассмотрим механизм электропроводности полупроводника с донорной пятивалентной примесью мышьяка As, которую вводят в кристалл, например, кремния. Пятивалентный атом мышьяка отдает четыре валентных электрона на образование ковалентных связей, а пятый электрон оказывается незанятым в этих связях Энергия отрыва (энергия ионизации) пятого валентного электрона мышьяка в кремнии равна 0,05 эВ = 0,08⋅10-19 Дж, что в 20 раз меньше энергии отрыва электрона от атома кремния. Поэтому уже при комнатной температуре почти все атомы мышьяка теряют один из своих электронов и становятся положительными ионами. Положительные ионы мышьяка не могут захватить электроны соседних атомов, так как все четыре связи у них уже укомплектованы электронами. В этом случае перемещения электронной вакансии — «дырки» не происходит и дырочная проводимость очень мала, т.е. практически отсутствует. Донорные примеси — это примеси легко отдающие электроны и, следовательно, увеличивающие число свободных электронов. При наличии электрического поля свободные электроны приходят в упорядоченное движение в кристалле полупроводника, и в нем возникает электронная примесная проводимость. В итоге мы получаем полупроводник с преимущественно электронной проводимостью, называемый полупроводником n-типа. (От лат. negativus — отрицательный). Поскольку в полупроводнике n-типа число электронов значительно больше числа дырок, то электроны являются основными носителями заряда, а дырки — неосновными. Акцепторная примесь От латинского «acceptor» — приемщик. В случае акцепторной примеси, например, трехвалентного индия In атом примеси может дать свои три электрона для осуществления ковалентной связи только с тремя соседними атомами кремния, а одного электрона «недостает». Один из электронов соседних атомов кремния может заполнить эту связь, тогда атом In станет неподвижным отрицательным ионом, а на месте ушедшего от одного из атомов кремния электрона образуется дырка. Акцепторные примеси, захватывая электроны и создавая тем самым подвижные дырки, не увеличивают при этом числа электронов проводимости. Основные носители заряда в полупроводнике с акцепторной примесью — дырки, а неосновные — электроны. Акцепторные примеси — это примеси, обеспечивающие дырочную проводимость. Полупроводники, у которых концентрация дырок превышает концентрацию электронов проводимости, называются полупроводниками р-типа (От лат. positivus — положительный.). Необходимо отметить, что введение примесей в полупроводники, как и в любых металлах, нарушает строение кристаллической решетки и затрудняет движение электронов. Однако сопротивление не увеличивается из-за того, что увеличение концентрации носителей зарядов значительно уменьшает сопротивление. Если в полупроводник одновременно вводятся и донорные, и акцепторные примеси, то характер проводимости полупроводника (n- или p-тип) определяется примесью с более высокой концентрацией носителей заряда.
К.2. Фотоэффект.законы столетова Явление было открыто в 1887г.Г.Герцом.Он-обнаружил, что при облучении ультра фиолетовым светом отриц.разрядника-ультр. лучами разряд происходит при меньшем напряжении между-электродами. Подробно это явление было исследовано в 1888 – 1890гг. А.Г. Столетовым. Схема опыта: К - металлич. пластина, отриц.Заряженафотокатод. М -мет.сетка, ТИ - токоизмерит. Прибор ИП - ист. пит Столетов обнаружил, что при-уменьшении Напряжения в разряднике, обуславливается выби-ванием под действием света из катодо-разрядника отриц. зарядов. При облучении светом фотокатода в цепи появляется ток, т.е. фототок. Фотоэлектр. Эффект – испускание электронов твердыми телами и жидк. Под-действием-эл/м излу-чения, в вакуум или др. среду. Внешний ФЭ – явление вырывания электронов из твердых тел под действием света. Экспериментально-было показано, что ВФЭ у металлов зависит не только от природы металла, но и от состояния его поверхности.
наличие фототока в области тормо-зящего напряжения – объясняется тем, что электроны обладают нач. кин. энергией сообщаемой светом. eU0= mV Iн=n*e; Iн-ток насыщения, пропорц. числу электронов вылетив. в единицу времени. Из ВАХ можно определить нач. кин. энергию и число электронов вырыв. светом из катода. Законы ВФЭ Столетова: 1 максим. начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности. 2.для каждого металла существует так называемая красная граница ФЭ(min частота света), ниже которой ФЭ не происходит.υ 0 – зависит от хим. природы металла и состояния его поверхности. 3.число-электронов выры-ваемых из катода за единицу времени пропорционально интенсивности света. ФЭ-практически безинерционен.При объяснении 1 и 2 закона с волновой точки зрения встретились трудности: ни наличие кр. границы ФЭ, ни не зависим. скорости электронов-от инте-нсивности, ни без инерциальность ФЭ, не может быть объяснено с точки зрения волновых представлений о свете. Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского или g) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой, длина волны при рассеянии меняться не должна, поскольку электрон под действием волны колеблется с частотой волны и излучает волны той же частоты. Объяснение эффекта Комптона даётся на основе квантовых представлений о природе света. Если считать, что излучение имеет корпускулярную природу, т.е. представляет собой поток фотонов, то эффект Комптона – результат упругого столкновения рентгеновских фотонов со свободными электронами вещества. В процессе столкновения фотон передаёт электрону часть своей энергии и импульса. Рассмотрим упругое столкновение двух частиц – налетающего фотона, обладающего импульсом pn = hn / c и энергией en = hn, с покоящимся свободным электроном (энергия покоя Wo = moc2). Фотон, столкнувшись с электроном, передаёт ему часть своей энергии и импульса и изменяет направление движения (т.е., рассеивается). Уменьшение энергии фотона означает увеличение длины волны (или уменьшение частоты) рассеянного излучения. Естественно, при упругом столкновении выполняются законы сохранения энергии и импульса. Согласно закону сохранения энергии: Wo + en = W + en’. Согласно закону сохранения импульса: pn = pe + pn’, где Wo = moc2 – энергия электрона до столкновения, en = hn - энергия налетающего фотона, W = moc2 + hn = Решая эти уравнения получим: moc2 (n - n’) = hnn’ (1 – cos q). Поскольку n = с / l, n’ = c / l’ и Dl = l’ - l, получим Dl = h/moc = lc – комптоновская длина волны (2.426 пм). Наличие в составе рассеянного излучения фотонов с исходными частотами объясняется соударениями фотонов со связанными электронами атома, что означает взаимодействие фотона как бы со всем атомом в целом. Поскольку атом намного тяжелее электрона, то переданная часть энергии атому, налетевшим фотоном, пренебрежимо мала и n» n’. Эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешние электроны нельзя считать свободными. Как эффект Комптона, так и фотоэффект обусловлены взаимодействием фотонов с электронами. В первом случае фотон рассеивается, во втором – поглощается. Рассеяние происходит при взаимодействии фотона со свободным электроном, а фотоэффект – со связанными электронами. При столкновении фотона со свободным электроном не может произойти поглощение фотона, поскольку это находилось бы в противоречии с законами сохранения – фундаментальными законами природы. Происходит именно рассеяние, то есть – эффект Комптона!
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.015 с.) |

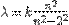 , где n = 3, 4, 5 и 6 соответственно для линий H α, H β, H γ, и H δ
, где n = 3, 4, 5 и 6 соответственно для линий H α, H β, H γ, и H δ

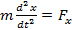 (1)
(1)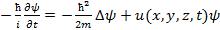 - временное ур-ие Шредингера, где m – масса мкч; U=U(x,y,z,t) – потенц-ая эн-я мкч.
- временное ур-ие Шредингера, где m – масса мкч; U=U(x,y,z,t) – потенц-ая эн-я мкч. 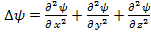 – оператор Лапласа
– оператор Лапласа , где Е –полная энерг-ия частицы.
, где Е –полная энерг-ия частицы.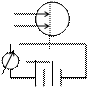
 Для характеристики используется ВАХ: (зависим. фототока от напряжения)
Для характеристики используется ВАХ: (зависим. фототока от напряжения)
 - энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем-то весьма значительна), en’ = hn’ – энергия рассеянного фотона. Подставив соответствующие значения в формулы законов сохранения, получим:
- энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем-то весьма значительна), en’ = hn’ – энергия рассеянного фотона. Подставив соответствующие значения в формулы законов сохранения, получим: P
P