
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое толкование волн де бройля.Содержание книги
Поиск на нашем сайте Физический смысл волн де Бройля заключ-ся в том, что интенсивность волн де Бройля в данной точке пространства пропорц-но вероятности обнаруженной частицы в этой точке простр-ва. Пояснение на основе опыта Тартаковского:
на Э наблюдалась дифр-я картина в виде пучок колец, при прохождении элект-ов через ме фольгу пучка электронов, они Э рассеивались. Точка 1–дифр-ый max–электр-ы попадают – I=Imax Точка 2 - между дифр-ми max - электроны не попадают-I=0; и тогда IБ ~ ne – волна де Бройля будет пропорц-а числу электронов (ne) в данной точке попадания электронов. Таким образом, волны де Бройля имеют вероятностный характер и их наз-ют волнами вероятности. Де Бройлем было показано и в последствии подтверждено опытами по дифр-ии электронов, что уравнение волны де Бройля свободного электрона описывается следующей формулой: Ψ(x,y,z,t)=C ei (Eħ t - pħ r) (1) – функция описывающая движ-ие свободного электрона наз-ся волновой функцией. C –амплитуда волны де Бройля. Квадрат модуля волновой функции определяет вероятность местонахождения частицы в данной точке пространства в данный момент времени. для всех случаев движения микрочастиц не только свободных электронов используется для описания их состояния функция координат времени, квадрат модуля которой определяется плотностью вероятности или вероятности местонахождения в данной точке пространства.
Соотношение неопределенностей Гейзенберга. Для микрочастицы из-за наличия волновых свойств, не все физич-е величины характер-ие движ-ие микрочастицы могут быть одновременно измерены точно (например, корд-ты и проекции на эти оси-коорд. не могут определить). т.е. для квантовых частиц классическое описание может быть приемлемо с определенными ограничениями или неопределенностями. Докажем, что наличие у электрона волновых свойств приводит к этому; пусть нам известно положение микрочастицы движущейся вдоль оси Х с точностью до ∆х; учтем наличие волн-х св-в у частицы, тогда частицы-это волна де Бройля и
х волн-ой функции х х+∆х не равна нулю, лишь на промежутке ∆х. таким образом, волновая функция такой частицы может быть в виде волнового пакета соответствующего набору волн-ых векторов ∆kx. Волновой пакет - волн-я функция движущейся частицы, возможная локализация которой в каждый момент времени ограничена некоторой небольшой областью координат. Для ВП известно соотношение: ∆х ∆kx ≥1 (6); для 3-мерного ВП: ∆y ∆ky ≥1, ∆z ∆kz ≥1; p=ħ k → проекция импульса: px= ħ kx; py=ħ ky pz=ħ kz → ∆ px=ħ ∆kx (7). Выражение ∆kx,y,z из (7) и подставляем в (6): ∆х ∆px ≥ ħ соотношение неопределенностей ∆y ∆py ≥ ħ } (8) Гейзенберга для корд-ты и ∆z ∆pz ≥ ħ проекции имп-са на эту ось коорд. Из (8) → невозможно одновременно точно измерить корд-ты микрочастицы и проекции импульса на эту же ось координат; ∆х, ∆у, ∆z точности определения координаты частицы; px,y,z точности определения проекции импульса. когда размеры области движения частицы велики по сравнению с λБ частицы, то для описания движения частицы можно применить законы классической физики. однако если линейные размеры сравнимы с λБ , то законы и понятия классической физики теряют силу. Уравнение Шредингера. Уравн-е Шред-ра – основное уравнение квантовой механики. Квант-я механика – теория устанавливающая способописания и законы движ-я микрочастицы и их систем, а также связь величин характериз-х микроч-цу системы с физич-ми велич-ми, непосредственно измеренные на опыте. наличие волновых свойств микрочастицы не позволяет использовать ур-ие (1). Ур-ие движ-ия микрочастицы было предложено Шред-ом в 1926г. ψ = ψ(x,y,z,t)-(ВФ)→ уравнение движ-ия микрочастицы должно быть относительно этой функции → уравнение должно быть волновым, т.к. с его помощью мы должны объяснить эксперименты по дифракции микрочастицы.
Временное урвнение Шредингера: (2) – основное уравн-е нерелятивистской квантовой механики, т.е справедливо для любой частицы движ-ся со скоростью << скорости света.
Уравнение Шр-ра добавляется важными условиями, накладывающимися на ВФ: 1.ВФ должна быть конечна, однозначна и непрерывна. 2. Первые производные должны быть непрерывны. 3. функция должна быть квадратично интегрируема: -∞∫∞|Ψ|2 dV = const=1 Во многих случаях потенциальная энергия частицы зависит только от координаты, т.е. U=U(x,y,z). В этом случае можно получить стационарное уравнение Шредингера, в котором исключена зависимость ВФ от времени t.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.009 с.) |

 метал-я фольга
метал-я фольга след-но - амплитуда
след-но - амплитуда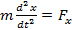 (1)
(1)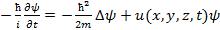 - временное ур-ие Шредингера, где m – масса мкч; U=U(x,y,z,t) – потенц-ая эн-я мкч.
- временное ур-ие Шредингера, где m – масса мкч; U=U(x,y,z,t) – потенц-ая эн-я мкч. 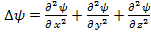 – оператор Лапласа
– оператор Лапласа , где Е –полная энерг-ия частицы.
, где Е –полная энерг-ия частицы.


