
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операторы в квантовой механикеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Гипотеза де Бройля утверждает существования волновых свойств у частиц. Опыты по дифракции подтверждают, если есть волновые свойства у объекта, то должна быть волновая функция отражающие эти свойства. Это Оператор-это любое математическое действие преобразующую некоторую функцию в другую функцию относящиеся к тому же классу. Простейшими операторами является сложения, умножение, дифференцирование, интегрирование. Операторы обозначаются
У оператора может быть такая функция которую он действуя на него не изменяет или в результате действия оператора получается та же функция, может быть умноженное на какое-то число, такая функция которая не изменяется при действия оператора называется собственной этого оператора, а число на которое она может быть умножено (она может быть=1) называется собственным значением данного оператора.
У одного оператора может быть несколько собственных функции со своими собственными значениями. Кроме того возможно, что одному собственному значению соответствует только одна собственная функция (состояние не вырожденное), а может быть одному собственному значению соответствует несколько Операторы можно складывать: Операторы можно умножать: Применение оператора начинается справа. Произведение операторов в общем случае не обладают свойством коммутитативности.
То есть результат последующих действий некоторых операторов из произведений зависит от очередности их применения.Но могут быть такие пары операторов, которые свойству коммуникативности удовлетворяют то есть результат их действия не зависит от очередности их применения. Такие операторы называются коммутирующими Среди операторов выделяют линейные операторы, такие операторы удовлетворяющие условия
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 функция, которой Борн дал статистическое толкование. Из формулы длины волны де Бройля следует, что импульс и координата не могут быть одновременно характеристиками состоянии частицы, но импульс и координата, это те характеристики, которые позволяют в классической механике определить траекторию движение частицы, то есть определить положение частицы в любое заданное момент времени. Если импульс и координата, не являются одновременно характеристиками состояния, то траекторию частицы построить нельзя, к такой частице понятие траектория вообще не применима. В квантовой механике не имеют смысла говорить о траектории, как о линии по которой движется частица, поэтому уравнение классической механики не применима в квантовой механике, говорят только о вероятности обнаружения частицы в том или в ином месте заданном момент времени
функция, которой Борн дал статистическое толкование. Из формулы длины волны де Бройля следует, что импульс и координата не могут быть одновременно характеристиками состоянии частицы, но импульс и координата, это те характеристики, которые позволяют в классической механике определить траекторию движение частицы, то есть определить положение частицы в любое заданное момент времени. Если импульс и координата, не являются одновременно характеристиками состояния, то траекторию частицы построить нельзя, к такой частице понятие траектория вообще не применима. В квантовой механике не имеют смысла говорить о траектории, как о линии по которой движется частица, поэтому уравнение классической механики не применима в квантовой механике, говорят только о вероятности обнаружения частицы в том или в ином месте заданном момент времени  , кроме того во многих случаях физической величины не могут принимать любые значения совокупность их возможных значениях (спектр) часто дискретный, а это означает не применимость операции интегрирования и дифференцирования. Из всего этого следует, что математический аппарат квантовой механики отличается от математического аппарата классической физики, ее математический аппарат операторы исчисление. В квантовой механике действия выполняются с операторами физических величин, а не самими физическими величинами.
, кроме того во многих случаях физической величины не могут принимать любые значения совокупность их возможных значениях (спектр) часто дискретный, а это означает не применимость операции интегрирования и дифференцирования. Из всего этого следует, что математический аппарат квантовой механики отличается от математического аппарата классической физики, ее математический аппарат операторы исчисление. В квантовой механике действия выполняются с операторами физических величин, а не самими физическими величинами. -титло.
-титло. 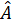 -оператор
-оператор  ,
,  -оператор координаты
-оператор координаты  ,
,  -оператор составляющих импульса.
-оператор составляющих импульса. (2.4.1.1)
(2.4.1.1) (2.4.1.2)
(2.4.1.2) (2.4.1.3)
(2.4.1.3)
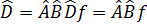
 (2.4.1.4)
(2.4.1.4) , коммутаторы
, коммутаторы  Важно, что коммутация или не коммутация операторов физических величин связано с возможностью одновременного определения соответствующих величин, то есть связано соотношением неопределенности. [20,21]
Важно, что коммутация или не коммутация операторов физических величин связано с возможностью одновременного определения соответствующих величин, то есть связано соотношением неопределенности. [20,21] . Линейные операторы имеют особые значение в квантовой физике, механике то есть соответствующие им собственные функции удовлетворяют принципу суперпозиции, то есть принципу которому удовлетворяет волновая функция
. Линейные операторы имеют особые значение в квантовой физике, механике то есть соответствующие им собственные функции удовлетворяют принципу суперпозиции, то есть принципу которому удовлетворяет волновая функция  . Среди операторов выделяют самосопряженные или эрмитовые операторы.
. Среди операторов выделяют самосопряженные или эрмитовые операторы.  две функции удовлетворяющие естественным условиям, то есть тем которым удовлетворяет волновая функция однозначность, дифференцированность, равенство нулю на бесконечности, квадратичные интегрированность и другие, то оператор
две функции удовлетворяющие естественным условиям, то есть тем которым удовлетворяет волновая функция однозначность, дифференцированность, равенство нулю на бесконечности, квадратичные интегрированность и другие, то оператор  называется самосопряженным, если
называется самосопряженным, если  интегрирование по всему пространству.
интегрирование по всему пространству. сопряжение, то есть замена
сопряжение, то есть замена  эрмитовые операторы имеют. В квантовой механике применяются только эрмитовые операторы, потому что у них собственное значение действие не мнимое.
эрмитовые операторы имеют. В квантовой механике применяются только эрмитовые операторы, потому что у них собственное значение действие не мнимое.


