
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельный переход от квантовой механики к классическойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Таблица-1. Операторы основных величин
Схема-6. Предельный переход квантовой механики к классический Содержание квантовой механики в контрольных вопросах Вопросы входного контроля
Квантовая механика занимает особое место в структуре физики, изучаемой в ВУЗе. Она представляет собой первую дисциплину, которая полностью посвящена вопросам формирования современной физики и некоторым проблемам, которые удалось решить на основе нерелятивистской квантовой механике Шредингера-Гейзенберга. Квантовая механика достаточно сложна для усвоения в связи с тем, что ее описание состояния физических систем и математический аппарат принципиально отличается от классической механики Ньютона и электродинамики Максвелла. Повышению качества освоения данного изучаемого предмета может способствовать представление его в виде системы вопросов, которые студенты могут использовать в процессе обучения, а преподаватель в процессе контроля. Система вопросов можно разделить на несколько групп.
· Пререквизиты. В эту группу включаются вопросы, актуализация знаний, по которым необходимо для изучения квантовой механики. В нее целесообразно включение вопросов классической физики: классической механики Ньютона-Галлилея, электродинамики Фарадея-Максвелла, а также вопросов, по которым классическая физика встретилась с затруднениями. Вопросы пререквизита могут быть использованы на этапе входного контроля, который проводится на первых неделях семестра и дает возможность студентам обратить внимание на вопросы, знание которых необходимо для успешного освоения изучаемой квантовой механики. Преподователь получает информацию об уровне знаний студентов, дает студентам необходимые рекомендации и делает выводы о дальнейших своих действиях. [22,23] · Вопросы для самоконтроля. Это группа вопросов относится к изучаемому курсу квантовой механике. Она включает в себя следующие разделы: ü библиография; знание имен ученых, внесших значительный вклад в развитие изучаемой дисциплины; ü основные понятия, величины, явления; ü законы и формулы; ü количественные задачи; Вопросы подготовлены на основе тестов используемых в различные годы при сдаче экзамена по тестовой форме контроля. К вопросам для самоконтроля приводятся ответы. · Задания для текущего и итогового контроля. Эти задания сформированы по трем видам: ü открытые тесты, составленные на основе вопросов для самоконтроля; разработано 5 вариантов по 30 вопросов для промежуточного контроля и 5 вариантов по 10 вопросов для итогового контроля; ü вопросы качественного характера, ответ на которые предполагает обзор некоторой проблемы или темы на уровне понимания без глубокого математического обоснования; разработано 25 вопросов такого типа; ü вопросы, требующие математического обоснования решения особо значимой проблемы квантовой механики; разработано 25 вопросов такого типа;
Пререквизиты. 1. Физика · Классическая физика: частицы и волны как принципиально различные объекты природы. · Характеристики состояния частиц в классической механике. Роль законов Ньютона в изучении механических систем. · Уравнения, описывающие движения частиц и распространения волн в классической физике. · Координаты импульс, энергия, момент импульса, магнитый момент- как характеристики частиц. · Двойственная природа света · Явления, подтверждающие волновые свойства света. · Явления, подтверждающие квантовые свойства света. · Структура атома. Модель Резерфорда. · Теория Бора. · Закон сохранения заряда в интегральной и дифференциальной формах. · Сила и энергия взаимодействия заряженных частиц. 2. Математика
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.125 (0.008 с.) |

 (2.5.1)
Показал, что импульс и координата не могут быть одновременно характеристиками сотояния, если учитывать волну де Бройля. Но именно на этих характеристиках построена классическая механика Ньютона. Они являются составляющими уравнения траектории движения частиц. К частице, обладающей волновыми свойствами, в принципе не применим. А это означает, что у такой частицы траектории не существует.
Классическая механика, разработанная Ньютоном, Гамильтоном, Якоби нашла широкое практическое применение, поэтому естественно возник вопрос о соотношении классической и квантовой механики. Квантовая механика является более общей теорией по отношению к классической подобно тому, как специальная теория относительности также является более общей по отношению к механике Ньютона. [22,23]
Более общая теория не отвергает менее общую, она только указывает границы ее применения. Например, если в формулах СТО учесть, что при
(2.5.1)
Показал, что импульс и координата не могут быть одновременно характеристиками сотояния, если учитывать волну де Бройля. Но именно на этих характеристиках построена классическая механика Ньютона. Они являются составляющими уравнения траектории движения частиц. К частице, обладающей волновыми свойствами, в принципе не применим. А это означает, что у такой частицы траектории не существует.
Классическая механика, разработанная Ньютоном, Гамильтоном, Якоби нашла широкое практическое применение, поэтому естественно возник вопрос о соотношении классической и квантовой механики. Квантовая механика является более общей теорией по отношению к классической подобно тому, как специальная теория относительности также является более общей по отношению к механике Ньютона. [22,23]
Более общая теория не отвергает менее общую, она только указывает границы ее применения. Например, если в формулах СТО учесть, что при  содержащих их слагаемых значительно меньше слагаемых, не содержающих это отношение и пренебреч ими, но из формул СТО получаются формулы классической механики.
содержащих их слагаемых значительно меньше слагаемых, не содержающих это отношение и пренебреч ими, но из формул СТО получаются формулы классической механики.
 (2.5.2)
Рассматривая квантовую и классическую механику можно различным образом определить условия предельного перехода от квантовой механики к классической. Классическая механика применима если можно пренебреч длиной волны де Бройля, то есть длина волны мала. Но, понятие мало - относительное. Длина волны де Бройля сравнивается с размером исследуемой системы.
(2.5.2)
Рассматривая квантовую и классическую механику можно различным образом определить условия предельного перехода от квантовой механики к классической. Классическая механика применима если можно пренебреч длиной волны де Бройля, то есть длина волны мала. Но, понятие мало - относительное. Длина волны де Бройля сравнивается с размером исследуемой системы.
 (2.5.3)
Из формулы де Бройля следует соотношение неопределенности:
(2.5.3)
Из формулы де Бройля следует соотношение неопределенности:
 (2.5.4)
(2.5.4)
 и
и  не могут быть одновременно характеристиками состояния, но они используются.
не могут быть одновременно характеристиками состояния, но они используются.  неопределенность координат, можно пренебреч если
неопределенность координат, можно пренебреч если  - неопределенность импульса, можно пренебреч, если
- неопределенность импульса, можно пренебреч, если  . Классическая механика применима, если
. Классическая механика применима, если  мала,
мала,  .
В классической механике величина, измеряемая Дж*с обозначается
.
В классической механике величина, измеряемая Дж*с обозначается  , не означает, что
, не означает, что  стало переменной. Эта запись означает, что в условиях данной задачи величина
стало переменной. Эта запись означает, что в условиях данной задачи величина  - содержит уравнение Якоби. Поэтому легче всего показать, что уравнение Шредингера переходит в уравнение Якоби.
- содержит уравнение Якоби. Поэтому легче всего показать, что уравнение Шредингера переходит в уравнение Якоби.
 (2.5.5)
(2.5.5)
 - радиус вектор выбранной частицы относительно системы отсчета.
- радиус вектор выбранной частицы относительно системы отсчета.
 (2.5.6)
(2.5.6)
 (2.5.7)
(2.5.7)
 (2.5.8)
(2.5.8)
 (2.5.9)
(2.5.9)
 (2.5.10)
Подставим в уравнение Шредингера и сократим на
(2.5.10)
Подставим в уравнение Шредингера и сократим на  .
.
 (2.5.11)
(2.5.11)
 (2.5.12)
При предельном переходе к классической механике слагаемое, содержащее сомножителем
(2.5.12)
При предельном переходе к классической механике слагаемое, содержащее сомножителем  , оказывается значительно меньше и им можно пренебреч.
, оказывается значительно меньше и им можно пренебреч.
 Схема-1. Развитие представлений о природе света
1.4
Схема-1. Развитие представлений о природе света
1.4  1.5
1.6 Схема-2. Атом
1.7
1.5
1.6 Схема-2. Атом
1.7  1.8
1.9 Схема-3. Двойственность природы
1.10
1.8
1.9 Схема-3. Двойственность природы
1.10  1.11
1.12 Схема-4. Волновое уравнение Шредингера
1.13
1.14
1.11
1.12 Схема-4. Волновое уравнение Шредингера
1.13
1.14  1.15 Схема-5. Математический аппарат
1.15 Схема-5. Математический аппарат





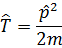




 -гaмильтониaн
-гaмильтониaн




