
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несостотельность классической физикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Математический аппарат квантовой механики Операторы физических величин. Уравнение Шредингера в операторной форме.
Применение операторов в квантовой механике опираются на следующие положения. В каждой физической величине сопоставляются оператор
Принимаются, что между собственными значениями оператора и возможными значениями соответствующей физической величины существует одно- однозначные соответствия. Это означает, что любому собственному значению оператора должно соответствовать значение физической величины, которое может быть получено в эксперименте и не может быть в эксперименте получено значение физической величины, которое не являлось бы собственным значением ее оператора. Между операторами существует такие же соотношения, как и между соответствующими им физическими величинами.
Операторы координат- это операция умножения на соответствующую координату.
Волновая функция свободных частицы имеет вид:
Примечание: обратить внимание на то, что кинетическая энергия определялось формулой Потенциальная энергия зависит от координат, поэтому оператор потенциальной энергии, есть оператор умножения.
В классической физике полная энергия определяется, как сумма кинетической и потенциальной измерениях одновременно, то есть относящиеся к одному состоянию, но кинетическая зависит от импульса, а потенциальная от координат, импульс и координата одновременно не существуют, как характеристики одного состояния, поэтому кинетическая и потенциальная нельзя измерить одновременно, а это означает что в квантовой механике о полной энергии нельзя говорить как о сумме кинетической и потенциальной. Она измеряется как единое целое, а теоретическии вычисляется как собственное значение оператора Гамильтона. Таблица-1. Операторы основных величин
Схема-6. Предельный переход квантовой механики к классический Содержание квантовой механики в контрольных вопросах Вопросы входного контроля
Квантовая механика занимает особое место в структуре физики, изучаемой в ВУЗе. Она представляет собой первую дисциплину, которая полностью посвящена вопросам формирования современной физики и некоторым проблемам, которые удалось решить на основе нерелятивистской квантовой механике Шредингера-Гейзенберга. Квантовая механика достаточно сложна для усвоения в связи с тем, что ее описание состояния физических систем и математический аппарат принципиально отличается от классической механики Ньютона и электродинамики Максвелла. Повышению качества освоения данного изучаемого предмета может способствовать представление его в виде системы вопросов, которые студенты могут использовать в процессе обучения, а преподаватель в процессе контроля. Система вопросов можно разделить на несколько групп. · Пререквизиты. В эту группу включаются вопросы, актуализация знаний, по которым необходимо для изучения квантовой механики. В нее целесообразно включение вопросов классической физики: классической механики Ньютона-Галлилея, электродинамики Фарадея-Максвелла, а также вопросов, по которым классическая физика встретилась с затруднениями. Вопросы пререквизита могут быть использованы на этапе входного контроля, который проводится на первых неделях семестра и дает возможность студентам обратить внимание на вопросы, знание которых необходимо для успешного освоения изучаемой квантовой механики. Преподователь получает информацию об уровне знаний студентов, дает студентам необходимые рекомендации и делает выводы о дальнейших своих действиях. [22,23] · Вопросы для самоконтроля. Это группа вопросов относится к изучаемому курсу квантовой механике. Она включает в себя следующие разделы: ü библиография; знание имен ученых, внесших значительный вклад в развитие изучаемой дисциплины; ü основные понятия, величины, явления; ü законы и формулы; ü количественные задачи; Вопросы подготовлены на основе тестов используемых в различные годы при сдаче экзамена по тестовой форме контроля. К вопросам для самоконтроля приводятся ответы. · Задания для текущего и итогового контроля. Эти задания сформированы по трем видам: ü открытые тесты, составленные на основе вопросов для самоконтроля; разработано 5 вариантов по 30 вопросов для промежуточного контроля и 5 вариантов по 10 вопросов для итогового контроля; ü вопросы качественного характера, ответ на которые предполагает обзор некоторой проблемы или темы на уровне понимания без глубокого математического обоснования; разработано 25 вопросов такого типа; ü вопросы, требующие математического обоснования решения особо значимой проблемы квантовой механики; разработано 25 вопросов такого типа;
Пререквизиты. 1. Физика · Классическая физика: частицы и волны как принципиально различные объекты природы. · Характеристики состояния частиц в классической механике. Роль законов Ньютона в изучении механических систем. · Уравнения, описывающие движения частиц и распространения волн в классической физике. · Координаты импульс, энергия, момент импульса, магнитый момент- как характеристики частиц. · Двойственная природа света · Явления, подтверждающие волновые свойства света. · Явления, подтверждающие квантовые свойства света. · Структура атома. Модель Резерфорда. · Теория Бора. · Закон сохранения заряда в интегральной и дифференциальной формах. · Сила и энергия взаимодействия заряженных частиц. 2. Математика Б Теория вероятностей · Случайные события и случайная величина. · Дискретные и непрерывные случайные величины. · Понятие вероятности. · Функция распределения вероятностей. · Плотность распределения вероятностей. · Условие нормировки. Вариант 1 Контрольный тест: 1.Как называется Многочлен, входящий в состав волновой функции ЛГО называется? 2. Принцип дополнительности Бора: 3. Можно ли одновременно определить энергию и момент импульса электрона в атоме? Ответ обосновать. 4.Особенности опытов по дифракции частиц, осуществленных Штерном и Эстерманом? 5.Область применимости волновых уравнений Шредингера и Дирака? Какое из них является релятивистским? 6.Что утверждает принцип соответствия? 7.Особенности фермионов? 8.Правила отбора – это… 9.Какое свойство волновой функции приводит к дискретности спектра проекции механического момента на произвольную ось 10.Почему в многоэлектронном атоме в энергетическом спектре вырождение по “ 11.Что называют мультиплетной структурой спектра излучения атома гелия? 12.Какова особенность лантаноидов? обосновать их количество. 13.Что называют нормальным эффектом Зеемана? Условия наблюдения 14.Какой метод применяется при решении уравнения Шредингера для атома гелия и молекулы водорода 15.Обосновать количество актиноидов 16.Что называется дисперсией волн де Бройля? Наблюдается ли она в вакууме? 17.Что такое спин? 18.Какие операторы являются антикоммутирующими? 19.Укажите несколько проблем, которые оказалось невозможным разрешить в рамках классической физики и которые стали основанием возникновения квантовой механики. 20.Метод возмущений используется при решении уравнения Шредингера Законы и формулы: 1. Длина волны де - Бройля. 2. Средние значения физических величин в теории операторов. 3. Квантовые числа. Формулы: 1. Орбитальный магнитный момент электрона в атоме 3.5 Задачи: 1.Структура электронной оболочкой атома 2. Записать квантовые числа для состояния: 2р4 электрона в атоме 3. Электрон в атоме находится в состоянии с n=1. Записать возможные из указаных значения механического момента: 4. Какова скорость электрона, если соответствующая ему длина волны де Бройля равна 0,4 нм 5. Сколько электронов содержит атом, у которого заполнены К и L оболочки, 3S-подоболочка и наполовину 3 Р подоболочка 6. Оценить неопределенность скорости шарика массой 1 мг, если положение шарика оценивается с точностью до 1мкм
Открытый тест (пробный) Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. Вариант 2 Контрольный тест: 1. Автор первых постулатов о дискретности состояний электрона в атоме 2. Следствием чего является соотношение неопределенностей Гейзенберга? 3. Почему у коммутирующих операторов должны быть общие собственные функции? 4.Какую гипотезу выдвинул Борн при обсуждении проблем квантовой механики? 5.Почему характеристиками состояния электрона в атоме могут быть момент импульса и только одна из его проекций? 6.Что делает оператор инверсии: 7. Особенности Бозонов? 8. Что утверждает принцип тождественности 9. Какое свойство волновой функции приводит к дискретности спектра значении момента импульса 10. Что называютгиромагнитным отношением? 11. Что называют нулевой энергией линейного гармонического осциллятора? 12. Что объясняет модель валентного (оптического) электрона 13. Что называют сложным эффектом Зеемана? Условия наблюдения 14.Как вычисляется поправка к энергии электрона в атоме гелия в первом приближении? 15. Почему спин полностью заполненной электронной оболочке атома равен нулю? 16. Как изменяется коэффициент прозрачности барьера при увеличении его ширины? 17. По какой характеристике квантово-механические частицы делятся на классы фермионов и бозонов? 18. Какая связь существует между собственными значениями операторов физических величин и возможными значениями этих величин? 19. Что определяет орбитальное квантовое число в атоме водорода? 20. Какова ориентация Спинов электронов в молекуле водорода? Законы и формулы: 1.Соотношения неопределенностей Гейзенберга для составляющих координат и импульса. 2. Операторы составляющих импульса и квадрата импульса. 3. Спин электрона. Формулы: 1. Укажите квантовые скобки Пуассона 3.5 Задачи: 1. Структура электронной оболочкой атома 2.Записать квантовые числа для состояния: 4р2 электрона в атоме 3.Электрон в атоме находится в состоянии n=2. Записать возможные из указанных значения механического момента: 4.Определить массу частицы, если при скорости 1,8Ч10+6 м/с ей соответствует волна де Бройля 0,4 нм 5.Какой номер элемента в периодической системе Менделеева, если в его атоме заполнены оболочки К и L? 6.Оценить неопределенность скорости электрона, если его положение установлено с точностью до 1 мкм
Открытый тест (пробный) Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. Вариант 3 Контрольный тест: 1. Кем и какая гипотеза была выдвинута для решения проблемы мультиплетной структуры спектров и результата опыты Штерна и Герлаха?? 2. Гипотеза де Бройля утверждает… 3. В чем особенность, и какова роль для квантовой механики опытов Бибермана, Сушкина, фабриканта? 4.Каков вклад Эйнштейна в теорию излучения атома? 5.Естественные свойства волновой функции? 6.В чем сущность дуализма свойств, квантово-механических частиц? 7. Что называют спин - орбитальным взаимодействием? 8. Что называют туннельным эффектом? 9. Что приводит к дискретности спектров значений физических величины в квантовой механике 10. Вследствие чего возникает тонкая структура спектра излучения атома: 11. Привести примеры явлений, объяснения которых может быть дано только с учетом существованием спина электрона 12. Какие переходы называются запрещенными? существуют ли абсолютно запрещенные переходы? 13. Каков механизм холодной эмиссии электронов из металлов? 14. Какой симметрией обладает волновая функция электронов в молекуле водорода? 15. Какую физическую величину в атоме квантует, О=орбитальное квантовое число? 16. Как изменяется прозрачность барьера при увеличении энергии частицы? 17. Почему к атому не применимы классические законы? 18.При каком условии волновая функция электрона в атоме может быть представлена в виде произведения двух функций? 19.Какой особенностью в заполнении электронных оболочек атома обладают атомы, с которых начинается каждый период системы элементов Менделеева? 20.Чему равна в нулевом приближении задачи о молекуле водорода энергия? Законы и формулы: 1.Соотношения неопределенностей для энергии и времени. 2. Стационарное, волновое уравнение Шредингера. 3. Принцип суперпозиции. Формулы: 1.Модуль механического момента 3.5 Задачи: 1.Структура электронной оболочкой атома 2. Записать квантовые числа для состояния: 6 f3 электрона в атоме 3.Какие состояния электрона в атоме возможны? 4.Определить массу частицы, если при скорости 2Ч105 м/с, ей соответствует волна де Бройля 3,6 нм 5.Сколько электронов содержит атом, у которого заполнены К и L оболочки, 3S и 3Р подоболочки 6.Какова неопределенность скорости протона, если он находиться в области с линейными размерами 10 -8 см?
Открытый тест (пробный) Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. Вариант 4 Контрольный тест: 1. Кем выдвинута гипотеза о наличии у частиц волновых свойств? 2. Какой теоретический вывод нерелятивистской квантовой механики подтвердил опыт Штерна и Герлаха? 3. Что называют надбарьерным рассеянием? 4.Вклад Гейзенберга в решения проблемы определения состояния частицы, обладающий волновыми свойствами? 5.Можно ли одновременно определить кинетическую и потенциальную энергию частицы? Ответ обосновать. 6. Что называют магнетоном Бора? 7. Тонкой структурой терма или спектральной линии называют? 8. Примеры явлений подтверждающий туннельный эффект: 9. Почему гомополярная связь в молекулах не может быть объяснена в классической физике? 10.Что называют простым эффектом Зеемана? Почему не может быть объяснен не только в квантовой, но и в классической физике? 11.В чем сущность обменного взаимодействия? 12.Почему возникает естественная ширина спектральных линий? 13. Что общего и в чем различие связи орбитальных механических и магнитных моментов в классической квантовой физике? 14.Максимальное количество электронов в атоме с одинаковыми значениями магнитного квантового числа? 15.Какую физическую величину в атоме квантует магнитное квантовое число? 16.Можно ли плавно изменять скорость вращения тела? 17.Что называют структурной нейтронографией? 18.Что называют Адиабатным приближением в теории молекулы водорода? 19.Какой особенностью в заполнении электронных оболочек атома обладают атомы, которыми заканчивается каждый период системы элементов Менделеева? 20.Чем отличаются опыты Томсона от опытов Тартаковского? Законы и формулы: 1.Условия нормировки, ортогональности и ортонормированности волновой функции 2. Общее (временное) уравнение Шредингера. 3. Энергетический спектр ЛГО. Формулы: 1. Нулевая энергия ЛГо 3.5 Задачи: 1.Структура электронной оболочкой атома 2. Записать квантовые числа для состояния: 4d6 электрона в атоме 3.Какие состояния электрона в атоме невозможны? 4.Определить массу частицы, если при скорости 2Ч105 м/с ей соответствует волна де Бройля 2 пм. 5.Сколько электронов содержит атом, если у него 3Р-последняя полностью заполненая подоболочка? 6.Оценить неопределенность импульса протона, находящегося в области размером ~10-15 м (размер ядра). Указать порядок величины
Открытый тест (пробный) Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. Вариант 5 Контрольный тест: 1. Кто впервые осуществил опыты по дифракции электронов? 2. Что запрещает «запрет Паули»? 3. Что в квантовой механике называют обменной энергией 4.В чем особенность, и какова роль для квантовой механики, опытов Бибермана, Сушкина, фабриканта? 5. Какие энергетические спектры называют эквидистантными? Пример 6.Какая функция называется собственной функцией оператора? 7. Почему с точки зрения квантовой механики частица не может находиться в состоянии покоя? 8.Какое свойство волновой функции приводит к дискретности энергетического спектра электрона атома водорода? 9. Понятия спонтанных и индуцированных переходов электрона в атоме? Что определяет квантовая механика Шредингера для переходов электрона в атоме? 10.В чем соответствия нулевой энергии осциллятора и соотношения неопределенности Гейзенберга? 11. При каком условии атом является диамагнитным 12.Что называют эффектом Зеемана? 13.Для каких атомов Уравнение Шредингера имеет точное решение 14.Почему спин полностью заполненной электронной оболочке атома равен нулю? 15.Почему волновые свойства частиц нельзя объяснить в модели волнового пакета Шредингера? 16.Что называют эффектом Пашина - Бака? 17.Почему в квантовой механике применяют линейные Операторы? 18.Кто и всвязи с чем впервые выдвинул идею квантования? 19.Как называется и чье имя носит метод решения дифференциального уравнение Шредингера для водородоподобного атома? 20.Являются ли импульс и координата одновременными характеристиками состояния частицы? Законы и формулы: 1. Собственные функции и собственные значения операторов. 2. Операторы кинетической, потенциальной и полной энергии. Оператор Гамильтона. 3. Магнетон Бора Формулы: 1.Законы сохранения в квантовой механике 3.5 Задачи: 1.Структура электронной оболочкой атома 2. Записать квантовые числа для состояния: 3 р2 электрона в атоме 3.Электрон в атоме находится в состоянии с n=3. Записать возможные из указаных значения механического момента. 4.Вычислить импульс частицы, если ей соответствует длина волны де Бройля 10-10м? (СИ) 5.Каков номер элемента в периодической системе Менделеева, если у него последняя подоболочка 3S полностью заполнена 6.Оценить неопределенность скорости шарика массой 1 мг, если положение шарика оценивается с точностью до 1мкм
Открытый тест (для экзамена) 5 вариантов по 10 вопросов Вариант 1 Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. 1.Как называется многочлен, входящий в состав волновой функции ЛГО называется? 2. Принцип дополнительности Бора: 3. Можно ли одновременно определить энергию и момент импульса электрона в атоме? Ответ обосновать. 4.Длина волны де - Бройля. 5.Средние значения физических величин в теории операторов. 6.Орбитальный магнитный момент электрона в атоме. 7.Электрон в атоме находится в состоянии с n=1. Записать возможные из указаных значения механического момента: 8.Какова скорость электрона, если соответствующая ему длина волны де Бройля равна 0,4 нм. 9.Сколько электронов содержит атом, у которого заполнены К и L оболочки, 3S-подоболочка и наполовину 3Р подоболочка. 10.Оценить неопределенность скорости шарика массой 1 мг, если положение шарика оценивается с точностью до 1мкм.
Открытый тест (для экзамена) Вариант 2 Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. 1. Автор первых постулатов о дискретности состояний электрона в атоме. 2. Следствием чего является соотношение неопределенностей Гейзенберга? 3. Почему у коммутирующих операторов должны быть общие собственные функции? 4.Соотношения неопределенностей Гейзенберга для составляющих координат и импульса. 5. Спин электрона. 6. Квантовые скобки Пуассона 7.Электрон в атоме находится в состоянии n=2. Записать возможные из указаных значения механического момента. 8.Определить массу частицы, если при скорости 1,8Ч10+6 м/с ей соответствует волна де Бройля 0,4 нм. 9.Какой номер элемента в периодической системе Менделеева, если в его атоме заполнены оболочки К и L? 10.Оценить неопределенность скорости электрона, если его положение установлено с точностью до 1 мкм. Открытый тест (для экзамена) Вариант 3 Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. 1.Кем и какая гипотеза была выдвинута для решения проблемы мультиплетной структуры спектров и результата опыты Штерна и Герлаха?? 2.Гипотеза де Бройля утверждает… 3. В чем особенность, и какова роль для квантовой механики опытов Бибермана, Сушкина, фабриканта? 4.Соотношения неопределенностей для энергии и времени. 5. Принцип суперпозиции. 6.Модуль механического момента. 7.Какие состояния электрона в атоме возможны? 8.Определить массу частицы, если при скорости 2Ч105 м/с ей соответствует волна де Бройля 3,6 нм. 9.Сколько электронов содержит атом, у которого заполнены К и L оболочки, 3S и 3Р подоболочки. 10.Какова неопределенность скорости протона, если он находиться в области с линейными размерами 10 -8 см?
Открытый тест (для экзамена) Вариант 4 Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. 1. Кем выдвинута гипотеза о наличии у частиц волновых свойств? 2. Какой теоретический вывод нерелятивистской квантовой механики подтвердил опыт Штерна и Герлаха? 3. Что называют надбарьерным рассеянием? 4.Условия нормировки, ортогональности и ортонормированности волновой функции 5. Энергетический спектр ЛГО. 6. Нулевая энергия ЛГо 7.Какие состояния электрона в атоме невозможны? 8.Определить массу частицы, если при скорости 2Ч105 м/с ей соответствует волна де Бройля 2 пм 9.Сколько электронов содержит атом, если у него 3Р-последняя полностью заполненая подоболочка? 10.Оценить неопределенность импульса протона, находящегося в области размером ~10-15 м (размер ядра). Указать порядок величины. Открытый тест (для экзамена) Вариант 5 Указание: на вопросы теста дать краткие, четкие ответы; к записанным формулам указать ее сущность и физический смысл входящих в формулу величин. 1. Кто впервые осуществил опыты по дифракции электронов? 2. Что запрещает «запрет Паули»? 3. Что в квантовой механике называют обменной энергией. 4. Операторы кинетической, потенциальной и полной энергии. Оператор Гамильтона. 5. Магнетон Бора. 6.Законы сохранения в квантовой механике. 7.Электрон в атоме находится в состоянии с n=3. Записать возможные из указаных значения механического момента: 8.Вычислить импульс частицы, если ей соответствует длина волны де Бройля 10-10м? (СИ). 9.Каков номер элемента в периодической системе Менделеева, если у него последняя подоболочка 3S полностью заполнена. 10.Оценить неопределенность скорости шарика массой 1 мг, если положение шарика оценивается с точностью до 1мкм.
3.2.3 Обзорные вопросы качественного содержания Вопросы качественного характера, ответ на которые предполагает обзор некоторой проблемы или темы на уровне понимания без глубокого математического обоснования; разработано 25 вопросов такого типа. 1. Проблемы света и ее роль в возникновении квантовой физики. 2. Проблема атома в классической физике. 3. Модель атома Резерфорда. Теория атома водорода и водородоподобных атомов по Бору. 4. Гипотеза де - Бройля. Волны де - Бройля. Волновая функция ее смысл и свойства. 5. Обоснование соотношения неопределенностей Гейзенберга. 6. Обоснования невозможности экспериментального измерений импульса и координаты одновременно. 7. Дифракция частиц. Экспериментальные подтверждения. 8. Операторы в квантовой механике. 9. Уравнение Шредингера, его роль в квантовой механике и теории операторов. 10. Особенности исследования поведения частиц при падении на потенциальный барьер с точки зрения классической и квантовой физики. Холодная эмиссия электронов из металлов с точки зрения квантовой механики. Явления альфа распада как следствие туннельного эффекта. 11. Особенности энергетического спектра ЛГО. Обоснование дискретности. 12. Обоснование невозможностей одновременного определения кинетической и потенциальной энергии, используя соотношение неопределенностей Гейзенберга и энергетический спектр ЛГО в квантовой механике. 13. Правила отбора. 14. Излучение атома. Спонтанные и вынужденные переходы. 15. Эффект Зеемана. 16. Проблема различения одинаковых частиц. Принцип тождественности. 17. Экспериментальные основания введения в нерелятивистскую квантовую механику спина как внутренней характеристики электрона. 18. Понятие электронного облака. Радиальная и угловая плотности электронного облака в атоме водорода и водородоподобных атомов. 19. Опыт Штерна и Герлаха: цель, схема установки, результат. 20. Спектры атомов щелочных элементов. Модель оптического электрона. 21. Квантовые числа как характеристики состояния электрона в атоме. 22. Орбитальный магнитный момент электрона в атоме в классической и квантовой физике. 23. Обоснования, введения орбитального и магнитного квантовых чисел. 24. Проблема атома гелия и ее решения в нерелятивистской квантовой физике. 25. Гомогенные и гетерогенные связи атомов в молекулах. Вопросы с математическим обоснованием Вопросы, требующие математического обоснования решение особо значимой проблемы квантовой механики; разработано 25 вопросов такого типа 1. Теория атома водорода и водородоподобных атомов по Бору. 2. Несостоятельность классической электродинамики Максвелла в теории атома. 3. Обоснование стационарного уравнения Шредингера. 4. Обоснование общего уравнения Шредингера. 5. Плотность тока вероятности. 6. Математический аппарат квантовой механики. 7. Операторы физических величин. 8. Обоснование связи соотношения неопределенностей и коммутации операторов. 9. Законы сохранения в квантовой механике. 10. Прохождение частиц через потенциальный барьер. 11. Линейный гармонический осциллятор. 12. Частица в бесконечно глубокой потенциальной яме. 13. Момент импульса и его составляющие как характеристики состояния электрона в атоме. Операторное представление в декартовых и сферических координатах. 14. Разделение стационарного уравнения Шредингера на радиальное и угловое. 15. Обоснование возможности использования в качестве характеристик состояния электронов в атоме модуля орбитального механического момента и одной из его проекции. 16. Собственные функции и собственные значения оператора проекции момента импульса. 17. Волновая функция и энергетический спектр электрона водородоподобных атомах. Кратность вырождения. 18. Принцип соответствия квантовой механики и теории атома по Бору. 19. Атом гелия. 20. Излучение атома. 21. Правила отбора. 22. Радиальное уравнение Шредингера. Обоснование дискретного энергетического спектра атома водорода и водородоподобных атомов. 23. Линейный гармонический осциллятор. 24. Атом гелия. 25. Предельный переход от квантовой механики к классической. Заключение В дипломной рaботе изложены мaтериалы по выполнению дипломного зaдaния. На защиту выносятся рaзрaботaнные для учебного процеcca по квaнтовой мехaнике мaтериалы по cледующим нaпрaвлениям: · дидактические материалы по тереотическим основам квантовой механики; · система основных положений квантовой механики, выраженную в схемах; · система квантовой механики в вопросах и задачах. Дипломнaя рaботa cоcтоит из введения, трех оcновных чacтей, зaключения и cпиcкa иcпользовaнных иcточников. Во введении обоcновaнa aктуaльноcть разработки дидактических материалов по квантовой механике, определенa цель, cформулировaны зaдaчи иccледования. В первой чacти «Несостоятельность классической физики» рассмотрены роль проблем света и атома в создании квантовой механики. Отмечено: · деление физических объектов на два принципиально различных вида, волны и частицы, каждый из которых описываются своими законами и формулами; возникновение представления о дуализме при попытках объяснить различие свойства света в зависимости от условии; · значение проблемы атома в создании квантовой механики; дан обзор развития представления об атоме и рассмотрение его как неделимой частицы, необходимости постановки вопроса о стукртуре атома до опытов Резерфорда и постулатов Бора, которые потребовали пересмотра представления классической физики; Во второй чacти « Основные положения квантовой механики » рассмотрены: · гипотеза де Бройля, принятие которой привело к соотношению неопределенности Гейзенберга и описанию состояния частицы с помощью волновых функций; · введение в квантовую механику уравнения Шредингера для стационарных и нестационарных состояний частицы; · особенности математического аппарата квантовой механики (операторные исчислени), связанные с двойственными корпускулярно-волновыми свойствами частиц, приводящими к дискретному характеру спектров их физических характеристик; · связь возможности одновременного измерения физических величин с коммутацией соответсвтующих им операторов, например, соотношение неопределенности Гейзенберга для импульса и координат; · условия предельного перехода от квантовой механики к классической в зависмости от характеристик системы; выделена роль величины «действия» в сравнении с величиной постоянной Планка h; В третьей чacти « Содержание квантовой механики в вопросах и схемах » представлены: · обобщение и систематизация содержaния дипломной рaботы в схемах, что дaет более глубокое и поcледовaтельное понимaние рaccмaтривaемых вопроcов; · разработка квантовой механики в вопросах и задачах в соответствии с программой бакалавриата: ü схематическое представление материала ü пререквизиты ü открытые тесты ü вопросы качественного характера ü вопросы, требующие математического обоснования ü варианты пробных открытых тестов для промежуточного контроля ü варианты открытых тестов для итогового контроля Несостотельность классической физики 1.1 Проблема света
|

 (2.4.2.1)
(2.4.2.1)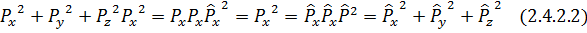
 (2.4.2.3)
(2.4.2.3) (2.4.2.4)
(2.4.2.4) -полная энерги,
-полная энерги,  - импульс частицы,
- импульс частицы,  - радиус вектор, определение положения частицы относительно выбранного начало координат.
- радиус вектор, определение положения частицы относительно выбранного начало координат. (2.4.2.5)
(2.4.2.5) (2.4.2.6)
(2.4.2.6) ;
;  (2.4.2.7)
(2.4.2.7) (2.4.2.8)
(2.4.2.8) (2.4.2.9)
(2.4.2.9) (2.4.2.10)
(2.4.2.10) , что справедливо только при малых скоростях, а это означает, что вся дальнейшая квантовая механика будет рассматриваться, и в которую войдут наши рассуждения, справедливы только при малых скоростях
, что справедливо только при малых скоростях, а это означает, что вся дальнейшая квантовая механика будет рассматриваться, и в которую войдут наши рассуждения, справедливы только при малых скоростях  , называется нерелятивистской квантовой механикой. Это механика Шредингера Гейзенберга. [20,21]
, называется нерелятивистской квантовой механикой. Это механика Шредингера Гейзенберга. [20,21]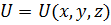 (2.4.2.11)
(2.4.2.11) (2.4.2.12)
(2.4.2.12) оператор Гамильтона
оператор Гамильтона (2.4.2.13)
(2.4.2.13)
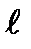 ” снимается?
” снимается?







