

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Основные положения квантовой механики
2.1 Двойственная природа частиц
2.1.1 Гипотеза де-Бройля
Решение проблемы атома началось с гипотезы де Бройля. Эта гипотеза утверждает, что не только свет, но и все материальные объекты обладают двойственной природой, то есть имеют и волновые и корпускулярные свойства. Тогда, он, используя свойства характеристики света в, 1924 году выдвинул гипотезу, что двойственность характерно не только для света, но и для любых тел и частиц.
 (2.1.1.1)
Он преполагает, что эти формулы применимы к любому объекту, свойственна некоторая длина волны, определяемая формулой: (2.1.1.1)
Он преполагает, что эти формулы применимы к любому объекту, свойственна некоторая длина волны, определяемая формулой:
 (2.1.1.2) (2.1.1.2)
 -длина волны соответствующей частице или телу имеющего импульс -длина волны соответствующей частице или телу имеющего импульс  . .  это длина волны де Бройля.[13]
Почему в классической физике не заметили, что частица не обладает свойствами волны?
Электрон это длина волны де Бройля.[13]
Почему в классической физике не заметили, что частица не обладает свойствами волны?
Электрон 
 (2.1.1.3) (2.1.1.3)
 В В  (2.1.1.4) (2.1.1.4)
 Возникает вопрос, почему волновые свойства частиц не замечают. Волновые свойства проявляются в интерференции и дифракции. Для их наблюдения необходимы условия. Для наблюдения дифракции волн необходимы препятствия, размеры которых сравнимы с длиной волны
Возникает вопрос, почему волновые свойства частиц не замечают. Волновые свойства проявляются в интерференции и дифракции. Для их наблюдения необходимы условия. Для наблюдения дифракции волн необходимы препятствия, размеры которых сравнимы с длиной волны  . Чтобы подтвердить гипотезу де Бройля, надо экспериментально показать, что для частиц характерно явление интерференции и дифракции. У рентгеновской лучей. Дифракция рентгеновских лучей к моменту гипотезы де Бройля уже была подтверждена, это была дифракция на кристаллах, поэтому опыты о дифракции частиц осуществлялись по методам разработанным для дифракции рентгеновских лучей.
2.1.2 Дифракция частиц
Основным свойством волны является спообность к дифракции и интерференции. Чтобы подтвердить экспериментально гипотезу де Бройля, необходимо знать порядок длины волны де Бройля, для того чтобы определить необходимые параметры постоянной дифракционной решетки. Для осуществления опыта необходим поток частиц, а потоки частиц сравнительно легко получаются, если частицы заряжены, они ускоряются под действием электрического поля. Если меньше масса частиц, тем больше длина волны де Бройля. Поэтому волновые свойства частиц, если они существуют, легче всего обнаружить на электронах, у них малые и есть электрические заряды. Поэтому первые опыты проводились на электронах. Для получения потока электронов использовалось их ускорение в электрическом поле за счет работы поля. . Чтобы подтвердить гипотезу де Бройля, надо экспериментально показать, что для частиц характерно явление интерференции и дифракции. У рентгеновской лучей. Дифракция рентгеновских лучей к моменту гипотезы де Бройля уже была подтверждена, это была дифракция на кристаллах, поэтому опыты о дифракции частиц осуществлялись по методам разработанным для дифракции рентгеновских лучей.
2.1.2 Дифракция частиц
Основным свойством волны является спообность к дифракции и интерференции. Чтобы подтвердить экспериментально гипотезу де Бройля, необходимо знать порядок длины волны де Бройля, для того чтобы определить необходимые параметры постоянной дифракционной решетки. Для осуществления опыта необходим поток частиц, а потоки частиц сравнительно легко получаются, если частицы заряжены, они ускоряются под действием электрического поля. Если меньше масса частиц, тем больше длина волны де Бройля. Поэтому волновые свойства частиц, если они существуют, легче всего обнаружить на электронах, у них малые и есть электрические заряды. Поэтому первые опыты проводились на электронах. Для получения потока электронов использовалось их ускорение в электрическом поле за счет работы поля.
 (2.1.2.1)
Характерным параметром, то есть постоянной решеткой в 1 (2.1.2.1)
Характерным параметром, то есть постоянной решеткой в 1  обладают кристаллы. У рентгеновских лучей также порядка обладают кристаллы. У рентгеновских лучей также порядка  . После их обнаружения для докозательства их волновой природы использовались опыты рентгеновских лучей их кристаллов. Поэтому опыты по дифракции частиц также осуществляется по тем же.[13,14]
Первым опытом по дифракции электронов был опыт- Дэвисона-Джемера, затем были опыты Томсона и Талтоновского, затем опыты Штермана-Эстевона. Опыты по дифракции подтвердили, что частицы обладают волновыми свойствами. Но это поставило вопрос о том, что такое волны де Бройля, какова их природа. Наличие темных полос в дифракционной картине света легко объясняется положением волн в противофазе. Но частицы друг друга уничтожать не могут, в связи с этим в физике возникла дискуссия, что такое волны де Бройля. Были самые различные предположения. Одно из предположений: в природе существуют только волны, а то, что воспринимается как частицы, рассматривается как волновой пакет.
Для понимания этого необходимо рассмотреть известное в механике биение. Оказывается, если накладываются механические волны в узком интервале частот . После их обнаружения для докозательства их волновой природы использовались опыты рентгеновских лучей их кристаллов. Поэтому опыты по дифракции частиц также осуществляется по тем же.[13,14]
Первым опытом по дифракции электронов был опыт- Дэвисона-Джемера, затем были опыты Томсона и Талтоновского, затем опыты Штермана-Эстевона. Опыты по дифракции подтвердили, что частицы обладают волновыми свойствами. Но это поставило вопрос о том, что такое волны де Бройля, какова их природа. Наличие темных полос в дифракционной картине света легко объясняется положением волн в противофазе. Но частицы друг друга уничтожать не могут, в связи с этим в физике возникла дискуссия, что такое волны де Бройля. Были самые различные предположения. Одно из предположений: в природе существуют только волны, а то, что воспринимается как частицы, рассматривается как волновой пакет.
Для понимания этого необходимо рассмотреть известное в механике биение. Оказывается, если накладываются механические волны в узком интервале частот  , то результирующая суммарная волна имеет амплитуду отличную от нуля, только в очень узкой области , то результирующая суммарная волна имеет амплитуду отличную от нуля, только в очень узкой области  . Эта узкая область называется волновой пакет. Существенно то, что они так и распространяются в пространстве. Предположим, что частицы, это волновые пакеты каких-то волн. Но это объяснение встретило затруднение. Дело в том, что волны обладают дисперсией, то есть зависимостью скорости от . Эта узкая область называется волновой пакет. Существенно то, что они так и распространяются в пространстве. Предположим, что частицы, это волновые пакеты каких-то волн. Но это объяснение встретило затруднение. Дело в том, что волны обладают дисперсией, то есть зависимостью скорости от  или или  . Электромагнитные волны в вакууме дисперсией не обладают. Волны любой длины распостраняются со скоростью. Поэтому если такой пакет возникнет из световых волн, то он может существовать сколь угодно долго. Но исследования показали, что существует дисперсия волн де Бройля даже в вакууме. То есть их скорость даже в вакууме зависит от . Электромагнитные волны в вакууме дисперсией не обладают. Волны любой длины распостраняются со скоростью. Поэтому если такой пакет возникнет из световых волн, то он может существовать сколь угодно долго. Но исследования показали, что существует дисперсия волн де Бройля даже в вакууме. То есть их скорость даже в вакууме зависит от  . Это означает, что если в какой-то момент пакет образуется, то в дальнейшем он будет расползаться, потому что волна каждой частоты движется со своей скоростью. . Это означает, что если в какой-то момент пакет образуется, то в дальнейшем он будет расползаться, потому что волна каждой частоты движется со своей скоростью.
 (2.1.2.2)
t- время расползания волнового пакета, b-размер частицы.
Представление о волновом пакете сохранилось в физике в некоторых расчетах. Но как природа волн де Бройля было отвернуто. В настоящее время принято статистическое толкование волн де Бройля, которое предложил Борн. Волны де Бройля это не материльные, а волны вероятности. Квадрат амплитуды волны де Бройля определяет вероятность нахождения частицы в данной области, в данный момент времени. А это означает, что частицы двигаются в пространстве, по законам отличаются от законов в классической механики.
2.1.3 Соотношение неопределенности Гейзенберга
Де Бройль выдвинул гипотезу о наличии волновых свойств соответствующие длиной волны. (2.1.2.2)
t- время расползания волнового пакета, b-размер частицы.
Представление о волновом пакете сохранилось в физике в некоторых расчетах. Но как природа волн де Бройля было отвернуто. В настоящее время принято статистическое толкование волн де Бройля, которое предложил Борн. Волны де Бройля это не материльные, а волны вероятности. Квадрат амплитуды волны де Бройля определяет вероятность нахождения частицы в данной области, в данный момент времени. А это означает, что частицы двигаются в пространстве, по законам отличаются от законов в классической механики.
2.1.3 Соотношение неопределенности Гейзенберга
Де Бройль выдвинул гипотезу о наличии волновых свойств соответствующие длиной волны.
 (2.1.3.1)
Справа и слева в формуле должны стоять величины, зависящие от одних переменных. Величина (2.1.3.1)
Справа и слева в формуле должны стоять величины, зависящие от одних переменных. Величина  зависит от формы волны и для обозначения ее величины необходим пространственный интервал не меньше длины волны. Это означает, что выражение длины волны в точке не имеет смысла. Математически это означает, что зависит от формы волны и для обозначения ее величины необходим пространственный интервал не меньше длины волны. Это означает, что выражение длины волны в точке не имеет смысла. Математически это означает, что  не функция не функция 
 (2.1.3.2)
Физически это означает, что говорить об импульсе в данной точке смысла не имеет. Скорость к точке относить нельзя.
Имульс и координата в классической физике оределяют состояние частиц. Зная координату и импульс (скорость) в некоторый момент времени (начальные условия) и силы, действующие на частицу можно узнать ее положение в любой момент времени, то есть построить траекторию. Понятие траектории, как линия, по которой движется тело, то есть совокупность точек, по которой оно проходит, является следствием принятия того, что у классической частицы принимается возможность одновременного.
Признание волны де Бройля, означает признание того, что в принципе импульс и координата не могут быть характеристиками состояния частицы, то есть не могут быть одновременно заданы. Это означает говорить к частицам обладающими волновыми свойствами, говорить о траектории не имеет смысла, не имеет смысла говорить об орбитах электрона в атом. (2.1.3.2)
Физически это означает, что говорить об импульсе в данной точке смысла не имеет. Скорость к точке относить нельзя.
Имульс и координата в классической физике оределяют состояние частиц. Зная координату и импульс (скорость) в некоторый момент времени (начальные условия) и силы, действующие на частицу можно узнать ее положение в любой момент времени, то есть построить траекторию. Понятие траектории, как линия, по которой движется тело, то есть совокупность точек, по которой оно проходит, является следствием принятия того, что у классической частицы принимается возможность одновременного.
Признание волны де Бройля, означает признание того, что в принципе импульс и координата не могут быть характеристиками состояния частицы, то есть не могут быть одновременно заданы. Это означает говорить к частицам обладающими волновыми свойствами, говорить о траектории не имеет смысла, не имеет смысла говорить об орбитах электрона в атом.
 (2.1.3.3)
Выражение (2.1.3.3)
Выражение  в массе смысла не имеет, чтобы говорить о в массе смысла не имеет, чтобы говорить о  необходима некоторая пространственная протяженность математики необходима некоторая пространственная протяженность математики  из формулы де Бройля следует, что из формулы де Бройля следует, что  не имеет смысла говорить о значении импульса в массе. Выражение не имеет смысла говорить о значении импульса в массе. Выражение  импульса не функция координат с точки зрения физики означает, что импульс и координата не могут одновременно характеризовать состояния объекта. Если в силу необходимости импульс и координата используется одновременно как характеристики состояния, то они определяются с некоторыми неопределенностями. Таким образом, у частицы, обладающие волновыми свойствами, импульс и координата не могут быть характеристиками состояния одновременно. Но в некоторых задачах возможно их использование, как харктеристику состояния. Но тогда они оба имеют некоторые неоределенности. Гейзенберг показал, что неопределенности одноименных состоящих импульса и координаты: импульса не функция координат с точки зрения физики означает, что импульс и координата не могут одновременно характеризовать состояния объекта. Если в силу необходимости импульс и координата используется одновременно как характеристики состояния, то они определяются с некоторыми неопределенностями. Таким образом, у частицы, обладающие волновыми свойствами, импульс и координата не могут быть характеристиками состояния одновременно. Но в некоторых задачах возможно их использование, как харктеристику состояния. Но тогда они оба имеют некоторые неоределенности. Гейзенберг показал, что неопределенности одноименных состоящих импульса и координаты:
 (2.1.3.4) (2.1.3.4)
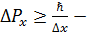 Если Если  точность измерения координаты, точность измерения координаты, 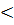 неопределенность неопределенность  , то неопределенность импульса будет также, чем более точна одна характеристика, то более неопределенной становится другая характеристика. В квантовой механике лучше говорить «неопределенность» чем, «не точность». Не точно можно уточнить, увеличить, а неопределенность следствие волновых свойств частиц и исключить ее нельзя. , то неопределенность импульса будет также, чем более точна одна характеристика, то более неопределенной становится другая характеристика. В квантовой механике лучше говорить «неопределенность» чем, «не точность». Не точно можно уточнить, увеличить, а неопределенность следствие волновых свойств частиц и исключить ее нельзя.
 (2.1.3.5)
Чем меньше неоределенность одной величины, тем больше неопределенная становится вторая величина. (2.1.3.5)
Чем меньше неоределенность одной величины, тем больше неопределенная становится вторая величина.
 (2.1.3.6) (2.1.3.6)
 -неоределеноость энергии, -неоределеноость энергии,  - продолжительность существования состояния энергии, которым измеряется. Обратить внимания на то, что неоределенность несвязана с неточностью измерения. Эта принципиальная неопрделенность, которую нельзя исключить повышению точности измерения. Вопрос о том, можно или нельзя определить - продолжительность существования состояния энергии, которым измеряется. Обратить внимания на то, что неоределенность несвязана с неточностью измерения. Эта принципиальная неопрделенность, которую нельзя исключить повышению точности измерения. Вопрос о том, можно или нельзя определить  импульс и координату характеристики состояния частиц в конечном счете должен решаться экспериментально. Можно ли в одном эксперименте измерить импульс и координату?[15,16,17]
Одним из противников квантовой механики был Эйнштейн. Поэтому он решил доказать измерить импульс, координату. Он предлагал схему приборов. Бор искал ошибку в тексте,- дискуссия Эйнштейна с Бором в конечном счете привела к тому, что большинство ученых признали квантовую механику. Анализ всех предлагаемых схем эксперимента привел к выводу о том, что в конечном счете все сводятся к схеме диафрагмы. Почему схема диафрагмы не позволяет одновременно импульс и координату? Бор анализируя сложившуюся ситуацию, пришел к выводу о том, что соотношение неопределенности относятся не только к импульсу и координату, для любой пары физических характеристик, следует задуматься, можно ли их определить одновременно.
Можно ли с точки зрения квантовой механики полную энергию определить как сумму кинетической и потенциальной? Бор сформулировал принцип дополнительности, утверждающий, что все физические величины делятся на 2 класса. Энергетические и координатно-временные. Одновременно характеризовать состояния могут только величины, относящиеся к одному классу. Эти 2 класса взаимно дополняют друг друга.
Примечание: соотношение неопределенности поставила проблему изменений. Оно заставило обратить внимание на то, что изменение это взаимодействие исследуемого объекта с прибором.
2.2 Волновая функция и ее смысл импульс и координату характеристики состояния частиц в конечном счете должен решаться экспериментально. Можно ли в одном эксперименте измерить импульс и координату?[15,16,17]
Одним из противников квантовой механики был Эйнштейн. Поэтому он решил доказать измерить импульс, координату. Он предлагал схему приборов. Бор искал ошибку в тексте,- дискуссия Эйнштейна с Бором в конечном счете привела к тому, что большинство ученых признали квантовую механику. Анализ всех предлагаемых схем эксперимента привел к выводу о том, что в конечном счете все сводятся к схеме диафрагмы. Почему схема диафрагмы не позволяет одновременно импульс и координату? Бор анализируя сложившуюся ситуацию, пришел к выводу о том, что соотношение неопределенности относятся не только к импульсу и координату, для любой пары физических характеристик, следует задуматься, можно ли их определить одновременно.
Можно ли с точки зрения квантовой механики полную энергию определить как сумму кинетической и потенциальной? Бор сформулировал принцип дополнительности, утверждающий, что все физические величины делятся на 2 класса. Энергетические и координатно-временные. Одновременно характеризовать состояния могут только величины, относящиеся к одному классу. Эти 2 класса взаимно дополняют друг друга.
Примечание: соотношение неопределенности поставила проблему изменений. Оно заставило обратить внимание на то, что изменение это взаимодействие исследуемого объекта с прибором.
2.2 Волновая функция и ее смысл
| Де Бройль выдвинул гипотезу опыты по дифракции, ее подтвердили. Возник вопрос: что такое волны де Бройля? Волна де Бройля- нематериальная, а волна вертикальности. Квадрат амплитуды волны определяет вертикальность данного состояния. Если есть волновые свойства у частиц, то должна быть волновая функция, определяющие эти свойства. Волновая функция играет одну из основных ролей в квантовой механике, поэтому важно определить ее свойства: определяет волну нематериальную, поэтому она содержит  Поскольку вертикальность- число действительное, то вертикальность определяется квадратом амплитуды по модулю. Поскольку вертикальность- число действительное, то вертикальность определяется квадратом амплитуды по модулю.
 (2.2.1) (2.2.1)
 (2.2.2) (2.2.2)

 имеет смысл плотности вертикальность обнаружения частицы в единичном около заданной точки имеет смысл плотности вертикальность обнаружения частицы в единичном около заданной точки  Если объем Если объем  - все пространство или вся область возможных знаний физических величин, то частицы обязательно будет обнаружены в этой области, то событие будет достоверным и его вероятность равна единице. Отсюда- это условие отлично используется для нахождения неопределенных коэффициентов в - все пространство или вся область возможных знаний физических величин, то частицы обязательно будет обнаружены в этой области, то событие будет достоверным и его вероятность равна единице. Отсюда- это условие отлично используется для нахождения неопределенных коэффициентов в  функции, из условия нормировки исследует что функция должна быть непрерывной, дифференциальной и квадратично интегрированной.[17,18]
Вертикальность- конечное числа функции, из условия нормировки исследует что функция должна быть непрерывной, дифференциальной и квадратично интегрированной.[17,18]
Вертикальность- конечное числа  функция должна быть конечной. Вертикальность конкретное состояние, она должна быть единственной. функция должна быть конечной. Вертикальность конкретное состояние, она должна быть единственной.  функция должна определять принцип суперпозиции. Принцип суперпозиции утверждает, что если возможны состояния с функциями функция должна определять принцип суперпозиции. Принцип суперпозиции утверждает, что если возможны состояния с функциями  , то возможно состояния определения координацией этих функций. , то возможно состояния определения координацией этих функций.
 -определяет вертикальность с которой данное состояние входит в суперпозицию. Например: функция описывают состояния электрона в атоме. Эти состояния могут быть различным с соответствующими коэффициентом -определяет вертикальность с которой данное состояние входит в суперпозицию. Например: функция описывают состояния электрона в атоме. Эти состояния могут быть различным с соответствующими коэффициентом  .
В механике рассматривается явление называемое биениями. Оно возникает при наложении волн с частотами в небольшом интервале .
В механике рассматривается явление называемое биениями. Оно возникает при наложении волн с частотами в небольшом интервале  - волновой пакет. Когда накладываются такие частицы, в результате оказывается что амплитуда результирующей волны достаточно велика в некоторой малой области и мала в остальной области. Важно, что эти системы так и распространяются в пространстве. Если частица обладает волновыми свойствами, то должна быть волновая функция, которая описывает эти свойства. Волновая функция или - волновой пакет. Когда накладываются такие частицы, в результате оказывается что амплитуда результирующей волны достаточно велика в некоторой малой области и мала в остальной области. Важно, что эти системы так и распространяются в пространстве. Если частица обладает волновыми свойствами, то должна быть волновая функция, которая описывает эти свойства. Волновая функция или  (Пси)- функция. Она может быть: (Пси)- функция. Она может быть:
 (2.2.4)
Волна де Бройля не материальная может содержать мнимую единицу. Но квадрат амплитуды определяет вероятность, а вероятность действительное число. Эта вероятность оределяет: (2.2.4)
Волна де Бройля не материальная может содержать мнимую единицу. Но квадрат амплитуды определяет вероятность, а вероятность действительное число. Эта вероятность оределяет:
 (2.2.5) (2.2.5)
 -комплексна сопряженная. Она получается из функции -комплексна сопряженная. Она получается из функции  заменой заменой 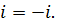 Поскольку смысл имеет произведение Поскольку смысл имеет произведение  , то в принципе не имеет значение у кого минус. , то в принципе не имеет значение у кого минус.  -вероятность обнаружения частицы в пределах объема -вероятность обнаружения частицы в пределах объема  около заданной точки. около заданной точки.  -вероятность обнаружения частицы в пределах заданного -вероятность обнаружения частицы в пределах заданного  . Если . Если  все пространство или известна, то это вероятность того, что частица находится где-то. А поскольку, говоря о существующей частице, то она обязательно где-то находится. Это событие достоверно. А вероятность достоверного события равна единице. Это условие нормировки все пространство или известна, то это вероятность того, что частица находится где-то. А поскольку, говоря о существующей частице, то она обязательно где-то находится. Это событие достоверно. А вероятность достоверного события равна единице. Это условие нормировки  функции. Таким образом из основных функции функции. Таким образом из основных функции  она должна удовлетворять условиям нормировки она должна удовлетворять условиям нормировки  функции. -функция должна удовлетврять условиям нормировки. Отсюда видно, что волновая функция должна быть интегрируемой, квадратичной. Волновые функции удовлетворяют принцип суперпозиции, если возможны состояния частицы, описываемые функциями ЭМИ функции. -функция должна удовлетврять условиям нормировки. Отсюда видно, что волновая функция должна быть интегрируемой, квадратичной. Волновые функции удовлетворяют принцип суперпозиции, если возможны состояния частицы, описываемые функциями ЭМИ  и и  , то возможно состояние, которое описывается функцией. Это называется суперпозицией состояния. , то возможно состояние, которое описывается функцией. Это называется суперпозицией состояния.  -определяет вероятность, с которой соответсвующее состояние входит в принцип суерпозиции.
2.3Волновое уравнение Шредингера
2.3.1 Стационарное уравнение Шредингера
Состояния частиц, обладающих волновыми свойствами, не может определяться импульсом и координатой, так как эти величины не существуют одновременно, что подтверждается тем, что они не могут быть измерены в одном эксперименте. Невозможность использования импульса и координаты как характеристики состояния приводят к невозможности применения законов классической механики Ньютона. Если частицы обладают волновыми свойствами, то и уравнения которые их описывают должны быть волновыми уравнениями. Волновые уравнения были известны в классической физике, поэтому естественно было проверить подходят ли они к описанию состояния частиц обладающих волновыми свойствами. Анализ волновых уравнений применительно квантовой механике частицам привел к следующим уравнениям. Состояния частицы описывают функции. В координатно - временном представлении она должна зависеть от времени и координат. -определяет вероятность, с которой соответсвующее состояние входит в принцип суерпозиции.
2.3Волновое уравнение Шредингера
2.3.1 Стационарное уравнение Шредингера
Состояния частиц, обладающих волновыми свойствами, не может определяться импульсом и координатой, так как эти величины не существуют одновременно, что подтверждается тем, что они не могут быть измерены в одном эксперименте. Невозможность использования импульса и координаты как характеристики состояния приводят к невозможности применения законов классической механики Ньютона. Если частицы обладают волновыми свойствами, то и уравнения которые их описывают должны быть волновыми уравнениями. Волновые уравнения были известны в классической физике, поэтому естественно было проверить подходят ли они к описанию состояния частиц обладающих волновыми свойствами. Анализ волновых уравнений применительно квантовой механике частицам привел к следующим уравнениям. Состояния частицы описывают функции. В координатно - временном представлении она должна зависеть от времени и координат.
 Если распределение вероятности состояния от времени не зависит, то функция стационарных состояний или координат часть
Если распределение вероятности состояния от времени не зависит, то функция стационарных состояний или координат часть  функции стационарных состояний функции стационарных состояний 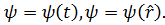 Искомое волновое уравнение должно описывать поведение функции, то есть его решением является функции. Анализ показал, что в случае стационарных состояний частица описывается уравнением: Искомое волновое уравнение должно описывать поведение функции, то есть его решением является функции. Анализ показал, что в случае стационарных состояний частица описывается уравнением:
 (2.3.1.2) (2.3.1.2)
 масса частицы, масса частицы, 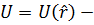 потенциальная энергия или точнее потенциальное поле, в котором находится частица. потенциальная энергия или точнее потенциальное поле, в котором находится частица.
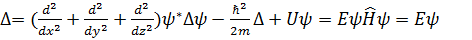 (2.3.1.3)
Решая это уравнение при заданном потенциале (2.3.1.3)
Решая это уравнение при заданном потенциале  , можно определить энергию , можно определить энергию  и волновую функцию и волновую функцию  , которое в этом уравнений является собственной функцией и собственным значением оператора Гамильтона.
Спектр собственных значений оператора может быть невырожденным: состояние , которое в этом уравнений является собственной функцией и собственным значением оператора Гамильтона.
Спектр собственных значений оператора может быть невырожденным: состояние  . Спектр может быть вырожденным: . Спектр может быть вырожденным:  . Таким образом, при решении уравнения Шредингера находятся совокупность возможных функции, которые определяют вероятности возможных состояний. Теоретическии вычисляются так же спектр собственных значений оператора Гамильтона, что соответствуют спектру возможных значений энергии частицы, при заданном потенциале . Таким образом, при решении уравнения Шредингера находятся совокупность возможных функции, которые определяют вероятности возможных состояний. Теоретическии вычисляются так же спектр собственных значений оператора Гамильтона, что соответствуют спектру возможных значений энергии частицы, при заданном потенциале  . Зависимость от потенциала . Зависимость от потенциала  , энергетический спектр может быть непрерывным или дискретным (спектр непрерывный у свободных частицы, при инфинитном движении неопределенности, и дискретный когда поле , энергетический спектр может быть непрерывным или дискретным (спектр непрерывный у свободных частицы, при инфинитном движении неопределенности, и дискретный когда поле  препятствия движения или ограничения движения, то есть движение финитное, ограниченное). Количество функции, то есть количество состояния соответствующих одному значению энергии, называется степенью или кратностью вырожденного спектра, обозначается препятствия движения или ограничения движения, то есть движение финитное, ограниченное). Количество функции, то есть количество состояния соответствующих одному значению энергии, называется степенью или кратностью вырожденного спектра, обозначается  или или  Де Бройль выдвинул гиотезу существование волновых свойств частиц. Опыты по дифракции электронов и более тяжелых частиц подтвердили гипотезу де Бройля. [17,18,19]
Примечание! При попытках истолкования результатов опытов по дифракции выдвигалась идея о том, что волновыми свойствами обладает не отдельная частица, а поток. В потоке происходят какие-то взаимодействия, которые приводят к появлению дифракционной картины, то есть к чередованию полос, в котором частицы поподают и не попадят.
В 1946 гоу в СССР Биберман, Сушкин, Фабрикант поставли эксперимент по дифракции электронов с использованием электронной пушки, которая выстрелировала электроны по одному. Таким образом, в пространстве от источника до экрана шел только один электрон. После того как было выпущено большое количество электронов, картина оказалась такой же, как, если бы они были выущены одновременно. А это значит, что волновыми свойствами обладает каждый отдельный электрон, а не поток. Волновые свойства описывают
Де Бройль выдвинул гиотезу существование волновых свойств частиц. Опыты по дифракции электронов и более тяжелых частиц подтвердили гипотезу де Бройля. [17,18,19]
Примечание! При попытках истолкования результатов опытов по дифракции выдвигалась идея о том, что волновыми свойствами обладает не отдельная частица, а поток. В потоке происходят какие-то взаимодействия, которые приводят к появлению дифракционной картины, то есть к чередованию полос, в котором частицы поподают и не попадят.
В 1946 гоу в СССР Биберман, Сушкин, Фабрикант поставли эксперимент по дифракции электронов с использованием электронной пушки, которая выстрелировала электроны по одному. Таким образом, в пространстве от источника до экрана шел только один электрон. После того как было выпущено большое количество электронов, картина оказалась такой же, как, если бы они были выущены одновременно. А это значит, что волновыми свойствами обладает каждый отдельный электрон, а не поток. Волновые свойства описывают  функции: функции:
 (2.3.1.4) (2.3.1.4)
 -радиус вектор точки относительно выбранно системы отсчета.
Уравнения Ньютона описывают состояния и движеня частиц, у которых состояния описываются одновременным заданием импульса и координаты -радиус вектор точки относительно выбранно системы отсчета.
Уравнения Ньютона описывают состояния и движеня частиц, у которых состояния описываются одновременным заданием импульса и координаты  . Если частица обладает волновыми свойствами, то импульс и координаты не могут быть характеристиками состояния. Следовательно, у такой частицы нет траектории. Следовательно, к такой частице законы Ньютона не пременимы. Законы, описывающие состояние кванто-механичеких частиц должны удовлетворять волновые уравнения. То есть вместо законов Ньютона должно быть волновое уравнение, которое позволяло бы определять распределения вероятностей состояния частицы в пространстве и во времени, то есть . Если частица обладает волновыми свойствами, то импульс и координаты не могут быть характеристиками состояния. Следовательно, у такой частицы нет траектории. Следовательно, к такой частице законы Ньютона не пременимы. Законы, описывающие состояние кванто-механичеких частиц должны удовлетворять волновые уравнения. То есть вместо законов Ньютона должно быть волновое уравнение, которое позволяло бы определять распределения вероятностей состояния частицы в пространстве и во времени, то есть  функции. И определять энергетический спектр частицы.
Волновые урвнения для квантовых частиц вводится путем анализа известных в механике волновых уравнений и выбора соответсвующего удовлетворяющего требованиям квантовой механики, то есть свойствам функции. И определять энергетический спектр частицы.
Волновые урвнения для квантовых частиц вводится путем анализа известных в механике волновых уравнений и выбора соответсвующего удовлетворяющего требованиям квантовой механики, то есть свойствам  функции. Таким уравнением оказалось дифференциальное волновое уравнение частных производных параболлического типа. Уравнения бывают элиптическое, парабалического, гиперболичессского.
Примечание! Обратить внимание на то, что при введении или обосновании уравнения использовалась формула кинетической энергии. функции. Таким уравнением оказалось дифференциальное волновое уравнение частных производных параболлического типа. Уравнения бывают элиптическое, парабалического, гиперболичессского.
Примечание! Обратить внимание на то, что при введении или обосновании уравнения использовалась формула кинетической энергии.
 (2.3.1.5)
Эта формула применим только к медленно движущимся частицам (2.3.1.5)
Эта формула применим только к медленно движущимся частицам  , то есть в области нерялитивствкой физики. Следовательно, записанное уравнение Шредингера является нерялитивитким и все дальнейшее, что основано на уравнение Шредингера, применим только в области малых скоростей. Поэтому полученные из уравнения Шредингера результаты могут не вполне соответствовать экспериментальным данным. В экспериментальных данных могут быть обнаружены релятивисткие эффекты, которые объясняет релятивисткая квантовая механика. , то есть в области нерялитивствкой физики. Следовательно, записанное уравнение Шредингера является нерялитивитким и все дальнейшее, что основано на уравнение Шредингера, применим только в области малых скоростей. Поэтому полученные из уравнения Шредингера результаты могут не вполне соответствовать экспериментальным данным. В экспериментальных данных могут быть обнаружены релятивисткие эффекты, которые объясняет релятивисткая квантовая механика.  - функция входящая в уравнение Шредингера должна удовлетворять всем естественным условиям. Однозначность, непрерывность, конечность не могут быть бесконечно большими для нахождения - функция входящая в уравнение Шредингера должна удовлетворять всем естественным условиям. Однозначность, непрерывность, конечность не могут быть бесконечно большими для нахождения 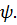 Из уравнения Шредингера необходимо, которое является дифференциальным уравнением 2-го порядка. Необходимо провести двойное интегрирование. При этом появляются неопределенные константы интегрировании для придания определенности, то есть однозначности функции Из уравнения Шредингера необходимо, которое является дифференциальным уравнением 2-го порядка. Необходимо провести двойное интегрирование. При этом появляются неопределенные константы интегрировании для придания определенности, то есть однозначности функции  необходимо из всех возможных значений неопределенных коэффициентов, необходимо выбрать те которые удовлетворяют условию нормировки, другим свойством необходимо из всех возможных значений неопределенных коэффициентов, необходимо выбрать те которые удовлетворяют условию нормировки, другим свойством  функции. Волновое уравнения Шреднгера зависит от энергии функции. Волновое уравнения Шреднгера зависит от энергии  . При этом может оказаться, что уравнение имеет решение при любых значениях . При этом может оказаться, что уравнение имеет решение при любых значениях  , то есть спектр значения , то есть спектр значения  нерерывный. А может быть так, что решение имеется только при дискретном ряде нерерывный. А может быть так, что решение имеется только при дискретном ряде  утверждается, что частица может иметь только не зачения энергии, при которых уравнения Шредингера имеют решения. Справедлива и обратная: все значения утверждается, что частица может иметь только не зачения энергии, при которых уравнения Шредингера имеют решения. Справедлива и обратная: все значения  , при которых уравнения имеют решения, могут быть реализованы в эксперименте.
2.3.2Общее (временнόе) уравнение Шредингера
Если , при которых уравнения имеют решения, могут быть реализованы в эксперименте.
2.3.2Общее (временнόе) уравнение Шредингера
Если  , то состояние будут нестационарными, тогда уравнение Шредингера принимает вид: , то состояние будут нестационарными, тогда уравнение Шредингера принимает вид:
 общее или временное уравнение Шредингера.
Примечание! общее или временное уравнение Шредингера.
Примечание!
 (2.3.2.1)
Возьмем (2.3.2.1)
Возьмем
 (2.3.2.2) (2.3.2.2)
 пси собственная функция оператора пси собственная функция оператора  , ,  собственное значение этого оператора. Получим ту же функцию. Значит она собственная. К функции применим оператор собственное значение этого оператора. Получим ту же функцию. Значит она собственная. К функции применим оператор  (производное по времени), результат умножили на (производное по времени), результат умножили на  . В результае получили ту же функцию . В результае получили ту же функцию  . Следовательно, функция . Следовательно, функция  является собственной функцией оератора является собственной функцией оератора  .
Если .
Если  функции стационарного состояния, то общее решение функции стационарного состояния, то общее решение  может быть записано так: может быть записано так:
 (2.3.2.3)
Примечание! При получении уравнения Шредингера из классических волновых уравнений по ходу получения использовалась формула: (2.3.2.3)
Примечание! При получении уравнения Шредингера из классических волновых уравнений по ходу получения использовалась формула:
 (2.3.2.4)
Но это формула применима только в малых скоростях, а это означает, что уравнение Шредингера применима для частиц, движущихся с малыми скоростями. Квантовая механика Шредингера и Гейзенберга не релятивистская. [19,20]
Примечание! Уравнение Шредингера является основой квантовой механики. Его выводить не из чего, то есть математические процедуры, которые делаются над классическими уравнениями, это просто подборка уравнения соответствовала экспериментальным данным, подобно тому, как не вводятся основ уравнения классической механики (2.3.2.4)
Но это формула применима только в малых скоростях, а это означает, что уравнение Шредингера применима для частиц, движущихся с малыми скоростями. Квантовая механика Шредингера и Гейзенберга не релятивистская. [19,20]
Примечание! Уравнение Шредингера является основой квантовой механики. Его выводить не из чего, то есть математические процедуры, которые делаются над классическими уравнениями, это просто подборка уравнения соответствовала экспериментальным данным, подобно тому, как не вводятся основ уравнения классической механики  .
Уравнение Шредингера отражает принцип причинности, то есть причинно, следственные связи подобно уравнениям Ньютона в классичекой механике. Состояние квантовой частицы оределяется только с некоторой вероятностью. Эту вероятность оределяют .
Уравнение Шредингера отражает принцип причинности, то есть причинно, следственные связи подобно уравнениям Ньютона в классичекой механике. Состояние квантовой частицы оределяется только с некоторой вероятностью. Эту вероятность оределяют  . Функция . Функция  из уравнения Шредингера определяется однозначно. Поэтому однозначно распределение вероятности состояния в класической механике, если известны начальные условия из уравнения Шредингера определяется однозначно. Поэтому однозначно распределение вероятности состояния в класической механике, если известны начальные условия  и и  и действующие силы, то можно однозначно определить скорость и положение частиы в пространстве, в любой момент в прошлом и будущем. Подобно этому в квантовой механике если задано распределение вероятностей. и действующие силы, то можно однозначно определить скорость и положение частиы в пространстве, в любой момент в прошлом и будущем. Подобно этому в квантовой механике если задано распределение вероятностей.  в момент в момент  и известно потенциальное поле и известно потенциальное поле  в котором находится частицы, то однозначно определено распределение вероятностей в котором находится частицы, то однозначно определено распределение вероятностей  , для любого момента времени , для любого момента времени 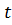 .Уравнения Шредингера дает решения для монохроматических волн. Общее решение определяется принципом суперпозиции.
2.3.3 Плотность тока вероятности. Закон сохранения частиц.
В электродинамике одним из основных законов является закон сохранения электрического заряда .Уравнения Шредингера дает решения для монохроматических волн. Общее решение определяется принципом суперпозиции.
2.3.3 Плотность тока вероятности. Закон сохранения частиц.
В электродинамике одним из основных законов является закон сохранения электрического заряда  , в дифференциальной форме. , в дифференциальной форме.
 (2.3.3.1) (2.3.3.1)
 объем плотности электрического заряда, объем плотности электрического заряда,  плотность тока плотность тока
 Здесь интегрирование идет по координатам, а производная вычисляется по времени.
Здесь интегрирование идет по координатам, а производная вычисляется по времени. 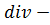 источник, источником тока является движущиеся заряды. источник, источником тока является движущиеся заряды.
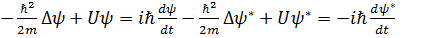 (2.3.3.3) (2.3.3.3)
 (2.3.3.4) (2.3.3.4)
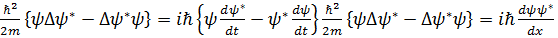 (2.3.3.5) (2.3.3.5)
 (2.3.3.6) (2.3.3.6)
 (2.3.3.7) (2.3.3.7)
 (2.3.3.8) (2.3.3.8)
 плотность электрического заряда, плотность электрического заряда,  плотность вероятности. плотность вероятности.
 (2.3.3.9) (2.3.3.9)
 закон сохранения количества числа частиц в квантовой механике. Этот закон означает, что в нерелятивистской квантовой механике рассматривается частицы, которые не рождаются, не уничтожаются, они уже существуют, если в какой то области количество частиц изменится, то есть поток частиц, или из этой области во внешней пространстве или из внешнего пространства в эту область. Характеристики квантово-механические частицы, как правила имеют дискретные спектры значения. Поэтому интегировать и дифференцировать их нельзя (интегрировать и деференцироать можно только непрерывные функции). Поэтому в квантовой механике выолняются не над самими величинами, не над их операторами. закон сохранения количества числа частиц в квантовой механике. Этот закон означает, что в нерелятивистской квантовой механике рассматривается частицы, которые не рождаются, не уничтожаются, они уже существуют, если в какой то области количество частиц изменится, то есть поток частиц, или из этой области во внешней пространстве или из внешнего пространства в эту область. Характеристики квантово-механические частицы, как правила имеют дискретные спектры значения. Поэтому интегировать и дифференцировать их нельзя (интегрировать и деференцироать можно только непрерывные функции). Поэтому в квантовой механике выолняются не над самими величинами, не над их операторами.
|
|



 (2.1.1.1)
Он преполагает, что эти формулы применимы к любому объекту, свойственна некоторая длина волны, определяемая формулой:
(2.1.1.1)
Он преполагает, что эти формулы применимы к любому объекту, свойственна некоторая длина волны, определяемая формулой:
 (2.1.1.2)
(2.1.1.2)
 -длина волны соответствующей частице или телу имеющего импульс
-длина волны соответствующей частице или телу имеющего импульс  .
.  это длина волны де Бройля.[13]
Почему в классической физике не заметили, что частица не обладает свойствами волны?
Электрон
это длина волны де Бройля.[13]
Почему в классической физике не заметили, что частица не обладает свойствами волны?
Электрон 
 (2.1.1.3)
(2.1.1.3)
 В
В  (2.1.1.4)
(2.1.1.4)
 Возникает вопрос, почему волновые свойства частиц не замечают. Волновые свойства проявляются в интерференции и дифракции. Для их наблюдения необходимы условия. Для наблюдения дифракции волн необходимы препятствия, размеры которых сравнимы с длиной волны
Возникает вопрос, почему волновые свойства частиц не замечают. Волновые свойства проявляются в интерференции и дифракции. Для их наблюдения необходимы условия. Для наблюдения дифракции волн необходимы препятствия, размеры которых сравнимы с длиной волны  . Чтобы подтвердить гипотезу де Бройля, надо экспериментально показать, что для частиц характерно явление интерференции и дифракции. У рентгеновской лучей. Дифракция рентгеновских лучей к моменту гипотезы де Бройля уже была подтверждена, это была дифракция на кристаллах, поэтому опыты о дифракции частиц осуществлялись по методам разработанным для дифракции рентгеновских лучей.
2.1.2 Дифракция частиц
Основным свойством волны является спообность к дифракции и интерференции. Чтобы подтвердить экспериментально гипотезу де Бройля, необходимо знать порядок длины волны де Бройля, для того чтобы определить необходимые параметры постоянной дифракционной решетки. Для осуществления опыта необходим поток частиц, а потоки частиц сравнительно легко получаются, если частицы заряжены, они ускоряются под действием электрического поля. Если меньше масса частиц, тем больше длина волны де Бройля. Поэтому волновые свойства частиц, если они существуют, легче всего обнаружить на электронах, у них малые и есть электрические заряды. Поэтому первые опыты проводились на электронах. Для получения потока электронов использовалось их ускорение в электрическом поле за счет работы поля.
. Чтобы подтвердить гипотезу де Бройля, надо экспериментально показать, что для частиц характерно явление интерференции и дифракции. У рентгеновской лучей. Дифракция рентгеновских лучей к моменту гипотезы де Бройля уже была подтверждена, это была дифракция на кристаллах, поэтому опыты о дифракции частиц осуществлялись по методам разработанным для дифракции рентгеновских лучей.
2.1.2 Дифракция частиц
Основным свойством волны является спообность к дифракции и интерференции. Чтобы подтвердить экспериментально гипотезу де Бройля, необходимо знать порядок длины волны де Бройля, для того чтобы определить необходимые параметры постоянной дифракционной решетки. Для осуществления опыта необходим поток частиц, а потоки частиц сравнительно легко получаются, если частицы заряжены, они ускоряются под действием электрического поля. Если меньше масса частиц, тем больше длина волны де Бройля. Поэтому волновые свойства частиц, если они существуют, легче всего обнаружить на электронах, у них малые и есть электрические заряды. Поэтому первые опыты проводились на электронах. Для получения потока электронов использовалось их ускорение в электрическом поле за счет работы поля.
 (2.1.2.1)
Характерным параметром, то есть постоянной решеткой в 1
(2.1.2.1)
Характерным параметром, то есть постоянной решеткой в 1  обладают кристаллы. У рентгеновских лучей также порядка
обладают кристаллы. У рентгеновских лучей также порядка  . После их обнаружения для докозательства их волновой природы использовались опыты рентгеновских лучей их кристаллов. Поэтому опыты по дифракции частиц также осуществляется по тем же.[13,14]
Первым опытом по дифракции электронов был опыт- Дэвисона-Джемера, затем были опыты Томсона и Талтоновского, затем опыты Штермана-Эстевона. Опыты по дифракции подтвердили, что частицы обладают волновыми свойствами. Но это поставило вопрос о том, что такое волны де Бройля, какова их природа. Наличие темных полос в дифракционной картине света легко объясняется положением волн в противофазе. Но частицы друг друга уничтожать не могут, в связи с этим в физике возникла дискуссия, что такое волны де Бройля. Были самые различные предположения. Одно из предположений: в природе существуют только волны, а то, что воспринимается как частицы, рассматривается как волновой пакет.
Для понимания этого необходимо рассмотреть известное в механике биение. Оказывается, если накладываются механические волны в узком интервале частот
. После их обнаружения для докозательства их волновой природы использовались опыты рентгеновских лучей их кристаллов. Поэтому опыты по дифракции частиц также осуществляется по тем же.[13,14]
Первым опытом по дифракции электронов был опыт- Дэвисона-Джемера, затем были опыты Томсона и Талтоновского, затем опыты Штермана-Эстевона. Опыты по дифракции подтвердили, что частицы обладают волновыми свойствами. Но это поставило вопрос о том, что такое волны де Бройля, какова их природа. Наличие темных полос в дифракционной картине света легко объясняется положением волн в противофазе. Но частицы друг друга уничтожать не могут, в связи с этим в физике возникла дискуссия, что такое волны де Бройля. Были самые различные предположения. Одно из предположений: в природе существуют только волны, а то, что воспринимается как частицы, рассматривается как волновой пакет.
Для понимания этого необходимо рассмотреть известное в механике биение. Оказывается, если накладываются механические волны в узком интервале частот  , то результирующая суммарная волна имеет амплитуду отличную от нуля, только в очень узкой области
, то результирующая суммарная волна имеет амплитуду отличную от нуля, только в очень узкой области  . Эта узкая область называется волновой пакет. Существенно то, что они так и распространяются в пространстве. Предположим, что частицы, это волновые пакеты каких-то волн. Но это объяснение встретило затруднение. Дело в том, что волны обладают дисперсией, то есть зависимостью скорости от
. Эта узкая область называется волновой пакет. Существенно то, что они так и распространяются в пространстве. Предположим, что частицы, это волновые пакеты каких-то волн. Но это объяснение встретило затруднение. Дело в том, что волны обладают дисперсией, то есть зависимостью скорости от  . Электромагнитные волны в вакууме дисперсией не обладают. Волны любой длины распостраняются со скоростью. Поэтому если такой пакет возникнет из световых волн, то он может существовать сколь угодно долго. Но исследования показали, что существует дисперсия волн де Бройля даже в вакууме. То есть их скорость даже в вакууме зависит от
. Электромагнитные волны в вакууме дисперсией не обладают. Волны любой длины распостраняются со скоростью. Поэтому если такой пакет возникнет из световых волн, то он может существовать сколь угодно долго. Но исследования показали, что существует дисперсия волн де Бройля даже в вакууме. То есть их скорость даже в вакууме зависит от  (2.1.2.2)
t- время расползания волнового пакета, b-размер частицы.
Представление о волновом пакете сохранилось в физике в некоторых расчетах. Но как природа волн де Бройля было отвернуто. В настоящее время принято статистическое толкование волн де Бройля, которое предложил Борн. Волны де Бройля это не материльные, а волны вероятности. Квадрат амплитуды волны де Бройля определяет вероятность нахождения частицы в данной области, в данный момент времени. А это означает, что частицы двигаются в пространстве, по законам отличаются от законов в классической механики.
2.1.3 Соотношение неопределенности Гейзенберга
Де Бройль выдвинул гипотезу о наличии волновых свойств соответствующие длиной волны.
(2.1.2.2)
t- время расползания волнового пакета, b-размер частицы.
Представление о волновом пакете сохранилось в физике в некоторых расчетах. Но как природа волн де Бройля было отвернуто. В настоящее время принято статистическое толкование волн де Бройля, которое предложил Борн. Волны де Бройля это не материльные, а волны вероятности. Квадрат амплитуды волны де Бройля определяет вероятность нахождения частицы в данной области, в данный момент времени. А это означает, что частицы двигаются в пространстве, по законам отличаются от законов в классической механики.
2.1.3 Соотношение неопределенности Гейзенберга
Де Бройль выдвинул гипотезу о наличии волновых свойств соответствующие длиной волны.
 (2.1.3.1)
Справа и слева в формуле должны стоять величины, зависящие от одних переменных. Величина
(2.1.3.1)
Справа и слева в формуле должны стоять величины, зависящие от одних переменных. Величина 
 (2.1.3.2)
Физически это означает, что говорить об импульсе в данной точке смысла не имеет. Скорость к точке относить нельзя.
Имульс и координата в классической физике оределяют состояние частиц. Зная координату и импульс (скорость) в некоторый момент времени (начальные условия) и силы, действующие на частицу можно узнать ее положение в любой момент времени, то есть построить траекторию. Понятие траектории, как линия, по которой движется тело, то есть совокупность точек, по которой оно проходит, является следствием принятия того, что у классической частицы принимается возможность одновременного.
Признание волны де Бройля, означает признание того, что в принципе импульс и координата не могут быть характеристиками состояния частицы, то есть не могут быть одновременно заданы. Это означает говорить к частицам обладающими волновыми свойствами, говорить о траектории не имеет смысла, не имеет смысла говорить об орбитах электрона в атом.
(2.1.3.2)
Физически это означает, что говорить об импульсе в данной точке смысла не имеет. Скорость к точке относить нельзя.
Имульс и координата в классической физике оределяют состояние частиц. Зная координату и импульс (скорость) в некоторый момент времени (начальные условия) и силы, действующие на частицу можно узнать ее положение в любой момент времени, то есть построить траекторию. Понятие траектории, как линия, по которой движется тело, то есть совокупность точек, по которой оно проходит, является следствием принятия того, что у классической частицы принимается возможность одновременного.
Признание волны де Бройля, означает признание того, что в принципе импульс и координата не могут быть характеристиками состояния частицы, то есть не могут быть одновременно заданы. Это означает говорить к частицам обладающими волновыми свойствами, говорить о траектории не имеет смысла, не имеет смысла говорить об орбитах электрона в атом.
 (2.1.3.3)
Выражение
(2.1.3.3)
Выражение  из формулы де Бройля следует, что
из формулы де Бройля следует, что  не имеет смысла говорить о значении импульса в массе. Выражение
не имеет смысла говорить о значении импульса в массе. Выражение  (2.1.3.4)
(2.1.3.4)
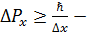 Если
Если  точность измерения координаты,
точность измерения координаты, 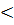 неопределенность
неопределенность  (2.1.3.5)
Чем меньше неоределенность одной величины, тем больше неопределенная становится вторая величина.
(2.1.3.5)
Чем меньше неоределенность одной величины, тем больше неопределенная становится вторая величина.
 (2.1.3.6)
(2.1.3.6)
 -неоределеноость энергии,
-неоределеноость энергии,  - продолжительность существования состояния энергии, которым измеряется. Обратить внимания на то, что неоределенность несвязана с неточностью измерения. Эта принципиальная неопрделенность, которую нельзя исключить повышению точности измерения. Вопрос о том, можно или нельзя определить
- продолжительность существования состояния энергии, которым измеряется. Обратить внимания на то, что неоределенность несвязана с неточностью измерения. Эта принципиальная неопрделенность, которую нельзя исключить повышению точности измерения. Вопрос о том, можно или нельзя определить  Поскольку вертикальность- число действительное, то вертикальность определяется квадратом амплитуды по модулю.
Поскольку вертикальность- число действительное, то вертикальность определяется квадратом амплитуды по модулю.
 (2.2.1)
(2.2.1)
 (2.2.2)
(2.2.2)

 имеет смысл плотности вертикальность обнаружения частицы в единичном около заданной точки
имеет смысл плотности вертикальность обнаружения частицы в единичном около заданной точки  Если объем
Если объем  - все пространство или вся область возможных знаний физических величин, то частицы обязательно будет обнаружены в этой области, то событие будет достоверным и его вероятность равна единице. Отсюда- это условие отлично используется для нахождения неопределенных коэффициентов в
- все пространство или вся область возможных знаний физических величин, то частицы обязательно будет обнаружены в этой области, то событие будет достоверным и его вероятность равна единице. Отсюда- это условие отлично используется для нахождения неопределенных коэффициентов в  функции, из условия нормировки исследует что функция должна быть непрерывной, дифференциальной и квадратично интегрированной.[17,18]
Вертикальность- конечное числа
функции, из условия нормировки исследует что функция должна быть непрерывной, дифференциальной и квадратично интегрированной.[17,18]
Вертикальность- конечное числа  , то возможно состояния определения координацией этих функций.
, то возможно состояния определения координацией этих функций.
 -определяет вертикальность с которой данное состояние входит в суперпозицию. Например: функция описывают состояния электрона в атоме. Эти состояния могут быть различным с соответствующими коэффициентом
-определяет вертикальность с которой данное состояние входит в суперпозицию. Например: функция описывают состояния электрона в атоме. Эти состояния могут быть различным с соответствующими коэффициентом  .
В механике рассматривается явление называемое биениями. Оно возникает при наложении волн с частотами в небольшом интервале
.
В механике рассматривается явление называемое биениями. Оно возникает при наложении волн с частотами в небольшом интервале  - волновой пакет. Когда накладываются такие частицы, в результате оказывается что амплитуда результирующей волны достаточно велика в некоторой малой области и мала в остальной области. Важно, что эти системы так и распространяются в пространстве. Если частица обладает волновыми свойствами, то должна быть волновая функция, которая описывает эти свойства. Волновая функция или
- волновой пакет. Когда накладываются такие частицы, в результате оказывается что амплитуда результирующей волны достаточно велика в некоторой малой области и мала в остальной области. Важно, что эти системы так и распространяются в пространстве. Если частица обладает волновыми свойствами, то должна быть волновая функция, которая описывает эти свойства. Волновая функция или  (Пси)- функция. Она может быть:
(Пси)- функция. Она может быть:
 (2.2.4)
Волна де Бройля не материальная может содержать мнимую единицу. Но квадрат амплитуды определяет вероятность, а вероятность действительное число. Эта вероятность оределяет:
(2.2.4)
Волна де Бройля не материальная может содержать мнимую единицу. Но квадрат амплитуды определяет вероятность, а вероятность действительное число. Эта вероятность оределяет:
 (2.2.5)
(2.2.5)
 -комплексна сопряженная. Она получается из функции
-комплексна сопряженная. Она получается из функции  заменой
заменой 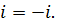 Поскольку смысл имеет произведение
Поскольку смысл имеет произведение  , то в принципе не имеет значение у кого минус.
, то в принципе не имеет значение у кого минус.  -вероятность обнаружения частицы в пределах объема
-вероятность обнаружения частицы в пределах объема  около заданной точки.
около заданной точки.  . Если
. Если  , то возможно состояние, которое описывается функцией. Это называется суперпозицией состояния.
, то возможно состояние, которое описывается функцией. Это называется суперпозицией состояния.  -определяет вероятность, с которой соответсвующее состояние входит в принцип суерпозиции.
2.3Волновое уравнение Шредингера
2.3.1 Стационарное уравнение Шредингера
Состояния частиц, обладающих волновыми свойствами, не может определяться импульсом и координатой, так как эти величины не существуют одновременно, что подтверждается тем, что они не могут быть измерены в одном эксперименте. Невозможность использования импульса и координаты как характеристики состояния приводят к невозможности применения законов классической механики Ньютона. Если частицы обладают волновыми свойствами, то и уравнения которые их описывают должны быть волновыми уравнениями. Волновые уравнения были известны в классической физике, поэтому естественно было проверить подходят ли они к описанию состояния частиц обладающих волновыми свойствами. Анализ волновых уравнений применительно квантовой механике частицам привел к следующим уравнениям. Состояния частицы описывают функции. В координатно - временном представлении она должна зависеть от времени и координат.
-определяет вероятность, с которой соответсвующее состояние входит в принцип суерпозиции.
2.3Волновое уравнение Шредингера
2.3.1 Стационарное уравнение Шредингера
Состояния частиц, обладающих волновыми свойствами, не может определяться импульсом и координатой, так как эти величины не существуют одновременно, что подтверждается тем, что они не могут быть измерены в одном эксперименте. Невозможность использования импульса и координаты как характеристики состояния приводят к невозможности применения законов классической механики Ньютона. Если частицы обладают волновыми свойствами, то и уравнения которые их описывают должны быть волновыми уравнениями. Волновые уравнения были известны в классической физике, поэтому естественно было проверить подходят ли они к описанию состояния частиц обладающих волновыми свойствами. Анализ волновых уравнений применительно квантовой механике частицам привел к следующим уравнениям. Состояния частицы описывают функции. В координатно - временном представлении она должна зависеть от времени и координат.
 Если распределение вероятности состояния от времени не зависит, то функция стационарных состояний или координат часть
Если распределение вероятности состояния от времени не зависит, то функция стационарных состояний или координат часть  функции стационарных состояний
функции стационарных состояний 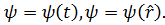 Искомое волновое уравнение должно описывать поведение функции, то есть его решением является функции. Анализ показал, что в случае стационарных состояний частица описывается уравнением:
Искомое волновое уравнение должно описывать поведение функции, то есть его решением является функции. Анализ показал, что в случае стационарных состояний частица описывается уравнением:
 (2.3.1.2)
(2.3.1.2)
 масса частицы,
масса частицы, 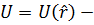 потенциальная энергия или точнее потенциальное поле, в котором находится частица.
потенциальная энергия или точнее потенциальное поле, в котором находится частица.
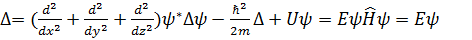 (2.3.1.3)
Решая это уравнение при заданном потенциале
(2.3.1.3)
Решая это уравнение при заданном потенциале  , можно определить энергию
, можно определить энергию  и волновую функцию
и волновую функцию  . Спектр может быть вырожденным:
. Спектр может быть вырожденным:  . Таким образом, при решении уравнения Шредингера находятся совокупность возможных функции, которые определяют вероятности возможных состояний. Теоретическии вычисляются так же спектр собственных значений оператора Гамильтона, что соответствуют спектру возможных значений энергии частицы, при заданном потенциале
. Таким образом, при решении уравнения Шредингера находятся совокупность возможных функции, которые определяют вероятности возможных состояний. Теоретическии вычисляются так же спектр собственных значений оператора Гамильтона, что соответствуют спектру возможных значений энергии частицы, при заданном потенциале  или
или  Де Бройль выдвинул гиотезу существование волновых свойств частиц. Опыты по дифракции электронов и более тяжелых частиц подтвердили гипотезу де Бройля. [17,18,19]
Примечание! При попытках истолкования результатов опытов по дифракции выдвигалась идея о том, что волновыми свойствами обладает не отдельная частица, а поток. В потоке происходят какие-то взаимодействия, которые приводят к появлению дифракционной картины, то есть к чередованию полос, в котором частицы поподают и не попадят.
В 1946 гоу в СССР Биберман, Сушкин, Фабрикант поставли эксперимент по дифракции электронов с использованием электронной пушки, которая выстрелировала электроны по одному. Таким образом, в пространстве от источника до экрана шел только один электрон. После того как было выпущено большое количество электронов, картина оказалась такой же, как, если бы они были выущены одновременно. А это значит, что волновыми свойствами обладает каждый отдельный электрон, а не поток. Волновые свойства описывают
Де Бройль выдвинул гиотезу существование волновых свойств частиц. Опыты по дифракции электронов и более тяжелых частиц подтвердили гипотезу де Бройля. [17,18,19]
Примечание! При попытках истолкования результатов опытов по дифракции выдвигалась идея о том, что волновыми свойствами обладает не отдельная частица, а поток. В потоке происходят какие-то взаимодействия, которые приводят к появлению дифракционной картины, то есть к чередованию полос, в котором частицы поподают и не попадят.
В 1946 гоу в СССР Биберман, Сушкин, Фабрикант поставли эксперимент по дифракции электронов с использованием электронной пушки, которая выстрелировала электроны по одному. Таким образом, в пространстве от источника до экрана шел только один электрон. После того как было выпущено большое количество электронов, картина оказалась такой же, как, если бы они были выущены одновременно. А это значит, что волновыми свойствами обладает каждый отдельный электрон, а не поток. Волновые свойства описывают  (2.3.1.4)
(2.3.1.4)
 . Если частица обладает волновыми свойствами, то импульс и координаты не могут быть характеристиками состояния. Следовательно, у такой частицы нет траектории. Следовательно, к такой частице законы Ньютона не пременимы. Законы, описывающие состояние кванто-механичеких частиц должны удовлетворять волновые уравнения. То есть вместо законов Ньютона должно быть волновое уравнение, которое позволяло бы определять распределения вероятностей состояния частицы в пространстве и во времени, то есть
. Если частица обладает волновыми свойствами, то импульс и координаты не могут быть характеристиками состояния. Следовательно, у такой частицы нет траектории. Следовательно, к такой частице законы Ньютона не пременимы. Законы, описывающие состояние кванто-механичеких частиц должны удовлетворять волновые уравнения. То есть вместо законов Ньютона должно быть волновое уравнение, которое позволяло бы определять распределения вероятностей состояния частицы в пространстве и во времени, то есть  (2.3.1.5)
Эта формула применим только к медленно движущимся частицам
(2.3.1.5)
Эта формула применим только к медленно движущимся частицам  , то есть в области нерялитивствкой физики. Следовательно, записанное уравнение Шредингера является нерялитивитким и все дальнейшее, что основано на уравнение Шредингера, применим только в области малых скоростей. Поэтому полученные из уравнения Шредингера результаты могут не вполне соответствовать экспериментальным данным. В экспериментальных данных могут быть обнаружены релятивисткие эффекты, которые объясняет релятивисткая квантовая механика.
, то есть в области нерялитивствкой физики. Следовательно, записанное уравнение Шредингера является нерялитивитким и все дальнейшее, что основано на уравнение Шредингера, применим только в области малых скоростей. Поэтому полученные из уравнения Шредингера результаты могут не вполне соответствовать экспериментальным данным. В экспериментальных данных могут быть обнаружены релятивисткие эффекты, которые объясняет релятивисткая квантовая механика. 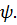 Из уравнения Шредингера необходимо, которое является дифференциальным уравнением 2-го порядка. Необходимо провести двойное интегрирование. При этом появляются неопределенные константы интегрировании для придания определенности, то есть однозначности функции
Из уравнения Шредингера необходимо, которое является дифференциальным уравнением 2-го порядка. Необходимо провести двойное интегрирование. При этом появляются неопределенные константы интегрировании для придания определенности, то есть однозначности функции  утверждается, что частица может иметь только не зачения энергии, при которых уравнения Шредингера имеют решения. Справедлива и обратная: все значения
утверждается, что частица может иметь только не зачения энергии, при которых уравнения Шредингера имеют решения. Справедлива и обратная: все значения  , то состояние будут нестационарными, тогда уравнение Шредингера принимает вид:
, то состояние будут нестационарными, тогда уравнение Шредингера принимает вид:
 общее или временное уравнение Шредингера.
Примечание!
общее или временное уравнение Шредингера.
Примечание!
 (2.3.2.1)
Возьмем
(2.3.2.1)
Возьмем
 (2.3.2.2)
(2.3.2.2)
 ,
,  собственное значение этого оператора. Получим ту же функцию. Значит она собственная. К функции применим оператор
собственное значение этого оператора. Получим ту же функцию. Значит она собственная. К функции применим оператор  (производное по времени), результат умножили на
(производное по времени), результат умножили на  . В результае получили ту же функцию
. В результае получили ту же функцию  . Следовательно, функция
. Следовательно, функция  .
Если
.
Если  функции стационарного состояния, то общее решение
функции стационарного состояния, то общее решение  может быть записано так:
может быть записано так:
 (2.3.2.3)
Примечание! При получении уравнения Шредингера из классических волновых уравнений по ходу получения использовалась формула:
(2.3.2.3)
Примечание! При получении уравнения Шредингера из классических волновых уравнений по ходу получения использовалась формула:
 (2.3.2.4)
Но это формула применима только в малых скоростях, а это означает, что уравнение Шредингера применима для частиц, движущихся с малыми скоростями. Квантовая механика Шредингера и Гейзенберга не релятивистская. [19,20]
Примечание! Уравнение Шредингера является основой квантовой механики. Его выводить не из чего, то есть математические процедуры, которые делаются над классическими уравнениями, это просто подборка уравнения соответствовала экспериментальным данным, подобно тому, как не вводятся основ уравнения классической механики
(2.3.2.4)
Но это формула применима только в малых скоростях, а это означает, что уравнение Шредингера применима для частиц, движущихся с малыми скоростями. Квантовая механика Шредингера и Гейзенберга не релятивистская. [19,20]
Примечание! Уравнение Шредингера является основой квантовой механики. Его выводить не из чего, то есть математические процедуры, которые делаются над классическими уравнениями, это просто подборка уравнения соответствовала экспериментальным данным, подобно тому, как не вводятся основ уравнения классической механики  .
Уравнение Шредингера отражает принцип причинности, то есть причинно, следственные связи подобно уравнениям Ньютона в классичекой механике. Состояние квантовой частицы оределяется только с некоторой вероятностью. Эту вероятность оределяют
.
Уравнение Шредингера отражает принцип причинности, то есть причинно, следственные связи подобно уравнениям Ньютона в классичекой механике. Состояние квантовой частицы оределяется только с некоторой вероятностью. Эту вероятность оределяют  . Функция
. Функция  и
и  и действующие силы, то можно однозначно определить скорость и положение частиы в пространстве, в любой момент в прошлом и будущем. Подобно этому в квантовой механике если задано распределение вероятностей.
и действующие силы, то можно однозначно определить скорость и положение частиы в пространстве, в любой момент в прошлом и будущем. Подобно этому в квантовой механике если задано распределение вероятностей.  в момент
в момент  и известно потенциальное поле
и известно потенциальное поле  в котором находится частицы, то однозначно определено распределение вероятностей
в котором находится частицы, то однозначно определено распределение вероятностей  , для любого момента времени
, для любого момента времени 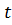 .Уравнения Шредингера дает решения для монохроматических волн. Общее решение определяется принципом суперпозиции.
2.3.3 Плотность тока вероятности. Закон сохранения частиц.
В электродинамике одним из основных законов является закон сохранения электрического заряда
.Уравнения Шредингера дает решения для монохроматических волн. Общее решение определяется принципом суперпозиции.
2.3.3 Плотность тока вероятности. Закон сохранения частиц.
В электродинамике одним из основных законов является закон сохранения электрического заряда  , в дифференциальной форме.
, в дифференциальной форме.
 (2.3.3.1)
(2.3.3.1)
 объем плотности электрического заряда,
объем плотности электрического заряда,  плотность тока
плотность тока
 Здесь интегрирование идет по координатам, а производная вычисляется по времени.
Здесь интегрирование идет по координатам, а производная вычисляется по времени. 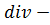 источник, источником тока является движущиеся заряды.
источник, источником тока является движущиеся заряды.
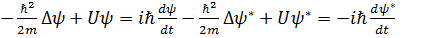 (2.3.3.3)
(2.3.3.3)
 (2.3.3.4)
(2.3.3.4)
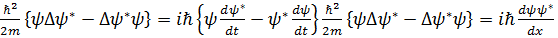 (2.3.3.5)
(2.3.3.5)
 (2.3.3.6)
(2.3.3.6)
 (2.3.3.7)
(2.3.3.7)
 (2.3.3.8)
(2.3.3.8)
 плотность вероятности.
плотность вероятности.
 (2.3.3.9)
(2.3.3.9)
 закон сохранения количества числа частиц в квантовой механике. Этот закон означает, что в нерелятивистской квантовой механике рассматривается частицы, которые не рождаются, не уничтожаются, они уже существуют, если в какой то области количество частиц изменится, то есть поток частиц, или из этой области во внешней пространстве или из внешнего пространства в эту область. Характеристики квантово-механические частицы, как правила имеют дискретные спектры значения. Поэтому интегировать и дифференцировать их нельзя (интегрировать и деференцироать можно только непрерывные функции). Поэтому в квантовой механике выолняются не над самими величинами, не над их операторами.
закон сохранения количества числа частиц в квантовой механике. Этот закон означает, что в нерелятивистской квантовой механике рассматривается частицы, которые не рождаются, не уничтожаются, они уже существуют, если в какой то области количество частиц изменится, то есть поток частиц, или из этой области во внешней пространстве или из внешнего пространства в эту область. Характеристики квантово-механические частицы, как правила имеют дискретные спектры значения. Поэтому интегировать и дифференцировать их нельзя (интегрировать и деференцироать можно только непрерывные функции). Поэтому в квантовой механике выолняются не над самими величинами, не над их операторами.



