Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операторы физических величинСодержание книги
Поиск на нашем сайте
Каждой физической величине Собственные значения оператора соответствуют возможным значениям физической величины. Собственные функции оператора соответствуют собственным состояниям, отвечающим выбранному собственному значению. Оператор энергии (гамильтониан) Векторный оператор импульса Квадрат оператора момента импульса Оператор
Оператор вектора спина Оператор Состояние электрона в атоме полностью определяется четыремя квантовыми числами
Пример Электрон в кулоновском поле ядра (атом водорода) Определить энергию электрона и волновые функции стационарных состояний. Решение: Пишем стационарное уравнение Шредингера Уравнение
имеет решение Вероятность нахождения электрона в основном состоянии в интервале
В ядре электрона нет, наибольшая вероятность нахождения электрона на расстоянии первого боровского радиуса, далее она падает по экспоненте. См рис 5
Рис.5 В общем случае уровни энергии соответствуют формуле Бора:
Волновая функция зависит от трех квантовых чисел
где Принцип Паули: В каждом квантовом состоянии может находится только один электрон. Пример. Заполнение квантовых состояний электронами происходит в соответствие с принципом минимума энергии и принципом Паули. При этом электроны заполняют низшие энергетические состояния группируясь в электронные оболочки ( равно
Так объясняется периодическая система химических элементов Д.И.Менделеева. Молекулы Молекула –наименьшая частица вещества обладающая его свойствами и состоящая из атомов соединенных химическими связями. Образование молекулы водорода. В первом приближении можно считать ядра атомов неподвижными и рассматривать только движение двух электронов. Если спины электронов антипараллельны то спин молекулы
Два атома водорода с антипараллельными спинами притягиваются образуют гомополярную молекулу водорода. Два атома водорода с параллельными спинами отталкиваются. График потенциальной энергии взаимодействия атомов водорода в зависимости от расстояния между электронами приведен на рис.6
Рис6 Энергия взаимодействия двух атомов водорода для триплетного и синглетного состояний. В синглетном состоянии образуется устойчивая молекула водорода (нижняя кривая) Молекулярные спектры Полная энергия молекулы может быть представлена в виде суммы квантованных значений энергии соответствующим трем видам её внутренних движений: электронов, колебаний атомов в молекуле. Вращению молекулы как целого.
Молекулярные спектры возникают при квантовых переходах между уровнями энергии молекулы Колебательные уровни энергии
Вращательные уровни энергии
Схема уровней энергии двухатомной молекулы показана на рис.7
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.103.169 (0.008 с.) |

 соответствует линейный эрмитовый оператор
соответствует линейный эрмитовый оператор  . Этот оператор принимает собственные значения
. Этот оператор принимает собственные значения  на базисе собственных функций
на базисе собственных функций  .
.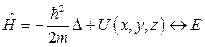 - энергия
- энергия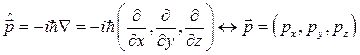 - импульс
- импульс
 -квадрат момента импульса
-квадрат момента импульса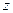 -компоненты момента импульса
-компоненты момента импульса

 -
- 




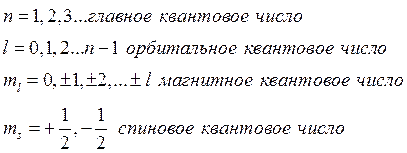
 . Задача обладает сферической симметрией. Поэтому используем сферические координаты
. Задача обладает сферической симметрией. Поэтому используем сферические координаты 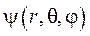 , Потенциальная энергия электростатического поля
, Потенциальная энергия электростатического поля 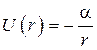 . Оператор Лапласа разделяем на радиальную и угловую части
. Оператор Лапласа разделяем на радиальную и угловую части  . Заменяем
. Заменяем  и получаем для радиальной части волновой функции
и получаем для радиальной части волновой функции  .
.
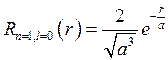
 :
: .
.


 -сферические гармоники.
-сферические гармоники.
 . На уровне энергии
. На уровне энергии  могут находится электрон в состоянии
могут находится электрон в состоянии  , и электрон в состоянии
, и электрон в состоянии  .Это атом гелия с двумя электронами. Атом лития имеет три электрона, поэтому два электрона находятся в состояниях
.Это атом гелия с двумя электронами. Атом лития имеет три электрона, поэтому два электрона находятся в состояниях  :
:  , один электрон находится в одном из двух состояний
, один электрон находится в одном из двух состояний  :
:  , остальные шесть состояний
, остальные шесть состояний  :
:  ,
, 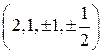 пустые.
пустые. ) от ядра наружу. Число электронов в оболочках
) от ядра наружу. Число электронов в оболочках 
 . Оболочки состоят из подоболочек:
. Оболочки состоят из подоболочек: ;
;  …
… если параллельны то
если параллельны то  Энергия взаимодействия двух электронов
Энергия взаимодействия двух электронов 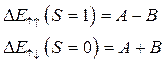
 -электростатическая энергия взаимодействия
-электростатическая энергия взаимодействия -обменная энергия (обмен электронами между состояниями)
-обменная энергия (обмен электронами между состояниями)


 где
где 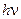 -квант испускаемого фотона частоты
-квант испускаемого фотона частоты 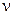 .
. где
где  колебательное квантовое число
колебательное квантовое число где
где  вращательное квантовое число,
вращательное квантовое число, 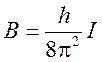 -вращательная постоянная,
-вращательная постоянная, 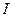 -момент инерции молекулы.
-момент инерции молекулы.