
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування задач лінійного програмування за допомогою ExcelСодержание книги
Поиск на нашем сайте
Спочатку розв’яжемо симплекс – методом за допомогою EXCEL економіко - математичну модель задачі планування виробництва, яка була першою сформульована у цьому розділі і вже розв’язана графічним методом у §2: f = 200 х1 + 300 х2 (max)
Згідно з планом попереднього параграфу 1. Зведемо цю задачу лінійного програмування до канонічної форми. Ввівши додаткові змінні х3, х4, х5, отримуємо f = 200 х1 + 300 х2 (max)
Запишемо її у електронну симплекс – таблицю:
Тут окрім стандартних стовпців симплекс – таблиці введений ще стовпець b/aij, у якому далі буде перевірятись умова допустимості. 2. Симплекс – таблиця виявляється приведеною до базису А3, А4, А5 опорного розв’язку. Це видно з того, що матриця такого розв’язку на стовпцях змінних х3, х4, х5 є діагональною, а оцінки основних змінних дорівнюють нулю. Отже, початковий опорний розв’язок α1 = (0; 0; 0; 0; 18; 30; 40), f (α1) = 0. 3. Серед оцінок базису є додатні, тож згідно з ознакою оптимальності α1 не є оптимальним і отже треба виконати крок симплекс – методу. 1) Вибираємо найбільшу додатну оцінку δ2 = 300. Зафарбуємо її в улюблений колір (тут червоний). Тим самим обрані змінна х2 і стовпець з номером 2 симплекс – таблиці. 2), 3) Елементи у стовпці 2 додатні, отже треба застосувати умову допустимості. У чарунок G2 електронної симплекс – таблиці введемо формулу = F2/B2, а далі скопіюємо (протягнемо) її у чарунки G3 і G4. В результаті дістанемо:
Мінімальне з отриманих значень Θ = 5 у чарунці G2. Зафарбуємо її бажано в той самий колір. Тим самим обрані рядок 1 (для якого саме і виконується умова допустимості) і ведучий елемент жорданова перетворення на перетині обраних рядка і стовпця у чарунку В2. Зафарбуємо також і його. 4) Жорданово перетворення: треба рядок 2 поділити на 20, а від кожного рядка з решти відняти отриманий, помноживши його на відповідне число у стовпці В. Задамо відповідні формули у стовпці В електронної симплекс – таблиці, а в решту скопіюємо з нього. Отже,
виокремимо нову симплекс – таблицю в діапазоні А7: G10. Надамо чарункам електронної таблиці таких значень:
Тут символ $ задає абсолютну адресацію: замість $В$2 можна задати прямо 20, замість $В$3 – 10. В результаті дістанемо:
5) Маємо симплекс – таблицю з новим набором основних змінних х2, х4, х5 (іншими словами з новим базисом), новий опорний розв’язок (0; 5; 0; 50; 15), нове значення цільової функції f = 1500. 6) На цьому перший крок симплекс – методу завершується. Треба розпочати другий крок з аналізу оцінок змінних і далі повторити всі попередні пункти. Другий крок. 1) У симплекс – таблиці, отриманій на першому кроці, залишилась одна додатна оцінка у чарунці А10 δ1 = 50, зафарбуємо її. Тим обрані змінна х1 і стовпець з номером 1 симплекс – таблиці. 2), 3) Елементи в обраному стовпці додатні, отже треба застосувати умову допустимості. У чарунок G7 електронної симплекс – таблиці введемо формулу = F2/B2 і скопіюємо її у чарунки G8 і G9. В результаті дістанемо:
Зафарбуємо мінімальне з отриманих значень Θ = 2 у чарунці G9. Зафарбуємо також на перетині обраних рядка і стовпця ведучий елемент жорданова перетворення у чарунці А9. 4) Жорданово перетворення: виокремимо нову симплекс – таблицю в діапазоні А12: G15. Надамо чарункам електронної таблиці таких значень:
Звичайно, що спочатку діємо у рядку 14, а потім у решті. В результаті дістанемо:
5) Маємо симплекс – таблицю з новим набором основних змінних х1, х2, х4 (іншими словами з новим базисом), новий опорний розв’язок (2; 4; 0; 20; 0), нове значення цільової функції f = 1600. 6) Нарешті всі оцінки не додатні. Згідно з теоремою 1 це означає, що розв’язок (2; 4; 0; 20; 0) і значення цільової функції f = 1600 є оптимальними. На цьому симплекс – метод завершує роботу. Загалом процес обчислень виглядає так:
Відкинувши три останні додані змінні, дістаємо розв’язок початкової задачі х1 = 2, х2 = 4, той самий, що і графічним методом. Цей розв’язок можна отримати і використавши надбудову EXCEL “Пошук розв’язку”. Ця надбудова задачі лінійного програмування розв’язує симплекс – методом, проте відразу видає оптимальний розв’язок до заданої математичної моделі. Спочатку запишемо дані задачі в електронну таблицю у форматі, схожому на формат симплекс – таблиці.
Тут у рядки 2,3,4 занесена матриця обмежень цієї задачі лінійного програмування, у рядку 5 до неї додані коефіцієнти цільової функції. Тепер додамо до цього у рядку 6 поточні значення змінних х1, х2 (зазвичай найбільш зручно х1 = 1, х2 = 1); у стовпці D відповідні значення лівих частин системи обмежень при поточних значеннях змінних. Тут у чарунці D2 задана формула =СУММПРОИЗВ(А2:В2;$А$6:$В$6), яка обчислює скалярний добуток масиву А2:В2 на масив А6:В6, тобто значення 10х1 + 20х2 при поточних значеннях змінних х1 = 1, х2 = 1. У чарунки D3:D5 цю формулу копіюємо. В результаті дістанемо:
У чарунці D5 тут значення цільової функції при поточних значеннях змінних, виділимо її і далі в термінології надбудови “Пошук розв’язку” будемо називати цільовою. Тепер час обрати Поиск решения у меню Сервис. (Якщо його нема в меню Сервис, то оберіть там команду Надстройки і у вікні діалогу Список надстроек встановіть прапорець Поиск решения). Адреса D5 з’явиться у полі Целевая ячейка вікна Поиск решения.
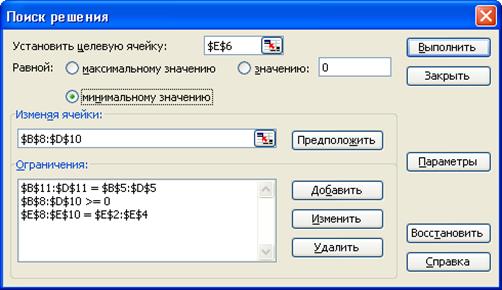
Після слова Равной: оберемо варіант максимальному значению. У поле Изменяя ячейки треба внести адресу змінних – діапазон А6:В6; виділимо його, коли курсор знаходиться у цьому полі, і ця адреса там з’явиться автоматично. У поле Ограничения треба внести систему обмежень. Натиснімо на кнопку Добавить, з’явиться наступне вікно діалогу:
Воно складається з трьох частин. У поле Ссылка на ячейку треба внести адресу чарунок, які містять значення лівих частин системи обмежень при поточних значеннях змінних, що підлягають обмеженню. Коли курсор знаходиться у цьому полі, виділимо чарунки D2:D4 і вони з’являться там. У центрі умова обмеження, яку треба вибрати із списку: в даному випадку це ≤. У поле Ограничение: треба внести його значення безпосередньо або адресу чарунки, де воно знаходиться. Коли курсор у цьому полі, виділимо чарунки С2:С4 і вони з’являться там. Тим самим задані три обмеження: 10х1 + 20х2 ≤ 100, 20х1 + 10х2 ≤ 100, 15х1 + 15х2 ≤ 90 одночасно. Натиснімо на Добавить, щоби прийняти ці обмеження і перейти до наступних. У системі обмежень ще залишилась умова хj ≥ 0 (j = 1,2). Так само внесемо у поле Ссылка на ячейку чарунки А6:В6, у центрі виберемо ≥ із списку, у полі Ограничение безпосередньо з клавіатури задамо 0.
Натиснімо на ОК, щоби прийняти ці обмеження і повернутись до вікна Поиск решения.
Тепер у цьому вікні вся економіко – математична модель даної задачі лінійного програмування: адреса цільової функції, вибір максимуму або мінімуму, адреса змінних, система обмежень. Натиснемо на Выполнить.
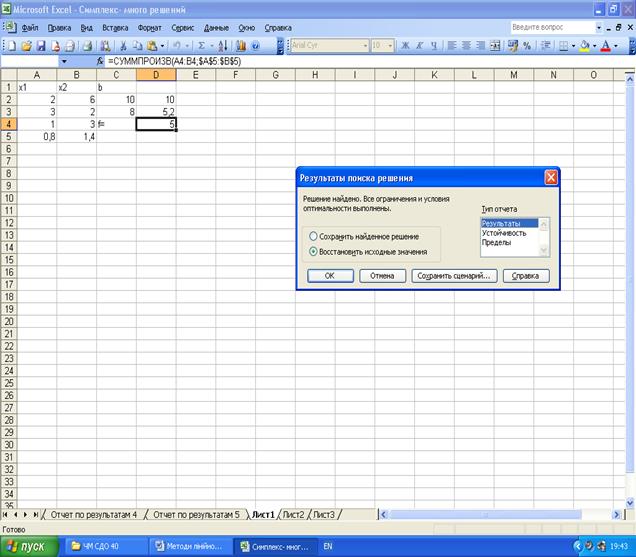
Відповідь можна знайти безпосередньо у чарунках змінних А6:В6 х1 = 2, х2 = 4, той самий, що і раніше. Вікно Результаты поиска решения повідомляє, що розв’язок знайдений при заданих обмеженнях. Якщо обрати Восстановить исходное значение, у полі Тип отчёта обрати Результаты і натиснути ОК, то у таблиці даних відтворяться початкові значення чарунок, а на окремому листі буде створений наступний звіт, який ми побачимо, якщо натиснути на Отчёт по результатам 1
По суті це відповідь даної задачі, створена у EXCEL. Розглянемо ще один приклад застосування надбудови Поиск решения – транспортну задачу, що була сформульована у §1. Це досить специфічний приклад задачі лінійного програмування, для розв’язання якої зазвичай використовують не симплекс – таблицю, а дещо іншу таблицю, яку і називають транспортною. Перш за все запишемо таку таблицю для даної задачі на лист EXCEL:
Фактично це таблиця вартості перевезень, наведена в умові задачі, до якої додані рядок попиту пунктів призначення знизу і праворуч стовпець ваги вантажу, що треба вивезти з пунктів відправлення. Для змінних – ваги вантажу, запланованого для перевезення з пункту Рi до пункту Мj (i, j = 1,2,3) – відведемо ще одну таблицю в діапазоні В8:D10, схожу на попередню. Як і раніше, зазвичай найбільш зручно у ці чарунки задати одиниці.
У чарунку В11 задамо формулу = СУММ(B8:B10) – це сумарна вага вантажу до пункту призначення М1: тут 3, оскільки всі змінні дорівнюють 1. (Можна виділити В11 і натиснути на ∑ (Автосумма) на стандартній панелі EXCEL і формула з’явиться там автоматично). Скопіюємо цю формулу у чарунки В12 і В13 для пунктів призначення М2 і М3. Аналогічно у чарунці Е8 формула =СУММ(B8:D8) – це сумарна вага вантажу з пункту відправлення Р1; скопіюємо цю формулу у чарунки Е9 і Е10 для Р2 і Р3. Рядок 6 під транспортною таблицею призначений для цільової функції, вартості в цій задачі (як це і у симплекс – таблиці). У чарунку В6 задамо формулу =СУММПРОИЗВ(B2:B4;B8:B10) – це вартість перевезень до М1 за даним планом перевезень, скопіюємо її у С6 і D6 для М2 і М3. У чарунку Е6 запишемо формулу = СУММ(B6:D6) – це значення цільової функції при поточних значеннях змінних, а Е6 в термінології надбудови “Пошук розв’язку” є цільовою чарункою. Виділимо її і тепер час обрати Поиск решения у меню Сервис.
У цьому вікні вся економіко – математична модель даної задачі лінійного програмування. А саме після слова Равной: обираємо варіант минимальному значению, тобто забезпечуємо вимогу, щоби загальна вартість перевезень була мінімальною. У поле Изменяя ячейки вносимо адресу змінних – діапазон В8:D10. У полі Ограничения (як і раніше, через вікно діалогу Добавление ограничений) виписана система обмежень цієї задачі, отримана у формульному вигляді в §1. Тут у першому рядку забезпечується вимога, щоби повністю був задоволений попит пунктів призначення; у третьому, щоби весь вантаж був вивезений з пунктів відправлення; у другому вимога невід’ємності змінних, тобто ваги вантажу. Натиснемо на Выполнить.
Вікно Результаты поиска решения повідомляє, що розв’язок знайдений при заданих обмеженнях. Оберемо Восстановить исходное значение і Результаты у полі Тип отчёта. Якщо тепер натиснути ОК, то у таблиці даних відтворяться початкові значення чарунок, а на окремому листі буде сформована відповідь, яку ми побачимо, якщо натиснути на Отчёт по результатам 1.
Отже, х11 = 3, х21 = 3, х31 = 0, х12 = 9, х22 = 0, х32 = 0, х13 = 0, х23 = 5, х33 = 10. У термінах початкової задачі це означає, що вага вантажу з Р1 до М1 3 т, з Р2 до М1 3 т, з Р3 до М1 0, з Р1 до М2 9 т, …; мінімальне можливе значення вартості дорівнює 91 грошовій одиниці.
Приклади Було б помилкою думати, що Поиск решения завжди дає остаточну відповідь на будь – яку задачу лінійного програмування. Розглянемо, наприклад, таку математичну модель
f = 3x2 + x1 (max)
Складемо відповідну електронну таблицю так, як у першому прикладі цього параграфу:
Дістанемо
Виділимо цільову чарунку D4 і оберемо Поиск решения у меню Сервис. Всю решту даних математичної моделі заносимо далі у це вікно. А саме після слова Равной: обираємо варіант максимальному значению, у поле Изменяя ячейки вносимо адресу змінних А5:В5. У полі Ограничения (як і раніше, через вікно діалогу Добавление ограничений) виписана система обмежень цієї задачі: нерівності 2х1 + 6х2 ≤ 10, 3х1 + 2х2 ≤ 8 у рядку 2, умова невід’ємності змінних у рядку 1.
Натиснемо на Выполнить. Дістанемо:
Оберемо Восстановить исходное значение і Результаты у полі Тип отчёта у вікні Результаты поиска решения. Натиснувши на ОК, дістанемо відповідь, яку побачимо, якщо натиснути на Отчёт по результатам 1.
Ніби – то все гаразд, але спробуємо розв’язати ту саму модель з іншими початковими значеннями змінних х1 = 1, х2 = 2. Відповідна електронна таблиця:
Виділимо цільову чарунку D4, оберемо Поиск решения у меню Сервис, всю решту даних математичної моделі заносимо далі у це вікно так само, як і раніше. Натиснемо на Выполнить і дістанемо:
Натиснувши на ОК, а потім на Отчёт по результатам 2, дістанемо відповідь:
Перший раз ми дістали х1 = 1,1, х2 = 1,3. Виявляється, що оптимальний розв’язок, який видає Поиск решения, залежить від початкових даних. Чи можливо таке насправді і як це збігається з теоремами, отриманими раніше? Розв’яжемо цю модель симплекс – методом. 1. Зведемо цю задачу до канонічної форми. Ввівши додаткові змінні х3, х4, отримуємо: f = 3x2 + x1 (max)
Запишемо її у електронну симплекс – таблицю:
2. Симплекс – таблиця виявляється приведеною до базису А3, А4 опорного розв’язку. Це видно з того, що матриця такого розв’язку на стовпцях змінних х3, х4 є діагональною, а оцінки основних змінних дорівнюють нулю. 3. Серед оцінок базису є додатні, тож згідно з ознакою оптимальності треба виконати крок симплекс – методу. 1) Вибираємо найбільшу додатну оцінку δ2 = 3. Зафарбуємо її у червоний колір. Тим самим обрані змінна х2 і стовпець з номером 2 симплекс – таблиці. 2), 3) Елементи у стовпці 2 додатні, отже треба застосувати умову допустимості. У чарунок F2 електронної симплекс – таблиці введемо формулу = E2/B2, а далі скопіюємо (протягнемо) її у чарунки F3 і F4. В результаті дістанемо:
Мінімальне з отриманих значень Θ = 1,666667 у чарунці F2. Зафарбуємо його і ведучий елемент жорданова перетворення на перетині обраних рядка і стовпця у чарунці В2. 4) Жорданово перетворення: виокремимо нову симплекс – таблицю в діапазоні А6: F8. Надамо чарункам електронної таблиці таких значень:
В результаті дістанемо:
5) Маємо симплекс – таблицю з новим набором основних змінних х2, х4 , новий опорний розв’язок (0; 1,7; 0; 4,7), нове значення цільової функції f = 5. 6) Всі оцінки не додатні. Згідно з теоремою 1 це означає, що розв’язок і значення цільової функції є оптимальними. На цьому симплекс – метод завершує роботу. Відкидаючи додаткові змінні, дістаємо х1 = 0, х2 ≈ 1,7. Тут те ж саме значення цільової функції, що й отримане за допомогою надбудови Поиск решения, проте ще один новий розв’язок, тут безумовно опорний. Зазначимо, що оцінка δ1 = 0, отже цільова функція, виражена через вільні змінні х1, х3 має вигляд f = 5 – 0,5х3. Тому, якщо обрати за нову основну змінну х1, то хоча її значення і стане додатним замість нульового, але значення цільової функції f не зміниться і ми дістанемо новий оптимальний опорний розв’язок. Отже, виконаємо ще одне жорданове перетворення. Елементи у стовпці 1 додатні, отже треба застосувати умову допустимості. В результаті дістанемо:
Новий опорний розв’язок (1;2; 0; 0), f = 5. Відкидаючи додаткові змінні, дістаємо х1 = 1, х2 = 2. Отже, існують принаймні два різних оптимальних опорних розв’язка. Зазвичай зрозуміти, проаналізувати ситуацію найкраще геометрично. На рисунку 4 множина Ω допустимих розв’язків – це чотирикутник OABCD, обмежений осями координат і прямими L1: 2х1 + 6х2 = 10 і L2: 3х1 + 2х2 = 8. Лінія нульового рівня цільової функції L0: f = х1 + 3х2 = 0 перетинає початок координат О(0;0) і перпендикулярна вектору нормалі N(1;3). Цей вектор перпендикулярний також і прямій L1, бо вектор нормалі N1(2;6) прямої L1 є колінеарним вектору N(1;3): 2 ∙ N = N1. Тому, як і на рисунку 2, існує нескінченна множина оптимальних розв’язків даної задачі – всі точки відрізка АВ. Вершини відрізка А(0;1,7) і В(2;1) – це якраз ті опорні розв’язки, які і були отримані симплекс – методом. Як виявляється, у такій задачі надбудова Поиск решения знаходить просто деякі точки на АВ залежно від початкових даних.
Ω L2
2,7 5 L0
Рисунок 4. Розглянемо ще один приклад математичної моделі. f = 3х1 + 2х2 (max)
Складемо відповідну електронну таблицю:
Дістанемо
Виділимо цільову чарунку D4 і оберемо Поиск решения у меню Сервис. Після слова Равной: обираємо варіант максимальному значению, у поле Изменяя ячейки вносимо адресу змінних А5:В5. У полі Ограничения: система обмежень цієї задачі: невід’ємність змінних у рядку 1, нерівність 2х1 + 3х2 ≥ 7 у рядку 2, 4х1 – 2х2 ≤ 7 у рядку 3.
Натиснемо на Выполнить. Дістанемо:
У вікні Результаты поиска решения повідомлення, що не відбулося збігу ітерацій, що і зрозуміло, бо надто великими є отримані результати: х1 = 31317472, х2 = 125269882, f = 3,44E+08 = 3,44∙108. Навряд чи прибуток перевершив 108, скоріше за все тут зовсім не існує розв’язка. Але чи так воно насправді? Розв’яжемо цю модель симплекс – методом. 1. Зведемо задачу до канонічної форми. Ввівши додаткові змінні х3, х4, отримуємо: f = 3x2 + 2x1 (max)
Запишемо її у електронну симплекс – таблицю:
2. На відміну від попередніх прикладів тут нема початкового опорного розв’язку: нема діагональної матриці. Насправді ж він є необхідним, щоби започаткувати симплекс – метод. Належний вигляд уже має стовпець змінної x4, до неї треба додати ще одну. Це не може бути x3 бо для такого опорного розв’язку x3 = – 7, тобто він не є допустимим. Це не може бути і x1. Справді, застосуємо умову допустимості, яка є необхідною і достатньою для того, щоби отриманий в результаті жорданова перетворення опорний розв’язок виявився допустимим. Тут min {7/4, 7/2} досягається у рядку 3, тобто якщо у якості ведучого рядка обрати необхідний нам другий, то ми знову отримаємо недопустимий опорний розв’язок. Залишилась змінна x2, ведучий елемент жорданова перетворення у чарунці В2. Отже, виокремимо нову симплекс – таблицю в діапазоні А6: F8. Надамо чарункам електронної таблиці таких значень:
В результаті дістанемо:
Тут є додатна оцінка δ3 = 2/3, а всі елементи стовпця С, окрім самої оцінки δ3 недодатні. Тому цільова функція не обмежена зверху (теорема 2, умова необмеженості цільової функції), тобто оптимального розв’язку даної задачі справді не існує. На рисунку 5 множина Ω допустимих розв’язків цієї задачі – це необмежений чотирикутник BACD, обмежений віссю координат Ох2 і прямими L1: 2х1 + 3х2 = 7 і L2: 4х1 – х2 = 7. Лінія нульового рівня
Ω L2
L0 C L1
О
Рисунок 5 цільової функції L0: f = 3х1 + 2х2 = 0 перетинає початок координат О(0;0) і перпендикулярна вектору нормалі N(3;2). Як і на рисунку 3, при пересуванні у напрямку вектора N пряма, паралельна L0 весь час буде перетинати область Ω, то цільова функція f не обмеж
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 911; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.182.126 (0.009 с.) |

 .
.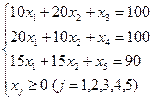






 .
.

 .
. х2
х2

 3 N(1;3)
3 N(1;3) 1,7 A
1,7 A L1
L1 B
B
 O 1 C х1
O 1 C х1 .
.

 .
. х2
х2 B D
B D


 A N(3;2)
A N(3;2) х1
х1


