
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия вращенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любая движущаяся система обладает кинетической энергией. ¨ Кинетическая энергия вращающегося тела равна половине произведения момента инерции тела на квадрат угловой скорости
Доказательство. Очевидно, что кинетическая энергия вращающегося тела (рис. 4.6)равна сумме кинетических энергий всех составляющих его материальных точек. ¨ Кинетическая энергия катящегося тела (рис. 4.7) складывается из кинетических энергий поступательного движения центра масс и вращения
Здесь: ¨ Задача 6. На тело, имеющее ось вращения Задание 1. Определить угловое ускорение
Задание 2. Определить угловую скорость Решение. Вращательное движение тела равноускоренное. Для такого движения угловая скорость определяется по формуле Задание 3. Определить момент импульса Решение. По определению момент импульса тела Задание 4. Определить работу Решение. Механическая работа вращательного движения определяется как Задание 5. Определить кинетическую энергию Решение. Кинетическая энергия вращательного движения определяется по формуле Задание 6. Определить работу Решение. Теорема о кинетической энергии:
Таблица соответствия характеристик
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.220.133 (0.005 с.) |

 .
. Разбив твердое тело на
Разбив твердое тело на 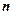 элементарных объемов массой
элементарных объемов массой  , движущихся со скоростями
, движущихся со скоростями  и расположенными на расстояниях
и расположенными на расстояниях  от оси вращения
от оси вращения  , получим
, получим  . Т.к. угловая скорость
. Т.к. угловая скорость  для всех точек тела одинакова, то
для всех точек тела одинакова, то  и
и  , где учтено, что
, где учтено, что  — момент инерции
— момент инерции  -ой материальной точки.
-ой материальной точки.
 .
. — масса тела,
— масса тела,  — скорость центра масс,
— скорость центра масс,  — момент инерции тела относительно оси вращения, проходящей через центр масс,
— момент инерции тела относительно оси вращения, проходящей через центр масс,  — угловая скорость относительно центральной оси.
— угловая скорость относительно центральной оси. и момент инерции
и момент инерции  2 кг×м2, действуют две касательные силы
2 кг×м2, действуют две касательные силы  Н и
Н и  4Н;
4Н; 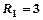 м — плечо первой силы;
м — плечо первой силы;  м — второй силы (рис. 4.8); начальная угловая скорость тела
м — второй силы (рис. 4.8); начальная угловая скорость тела  =5рад/с. Время
=5рад/с. Время  ,
,  с.
с. .
. Решение. По второму закону Ньютона для вращательного движения:
Решение. По второму закону Ньютона для вращательного движения: 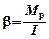 , где результирующий момент сил
, где результирующий момент сил  . Разность моментов объясняется тем, что
. Разность моментов объясняется тем, что  вращает тело (рис. 4.8) против хода часовой стрелки, а
вращает тело (рис. 4.8) против хода часовой стрелки, а  — по ходу. По определению модули моментов
— по ходу. По определению модули моментов  (Н×м),
(Н×м), 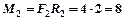 (Н×м), поэтому
(Н×м), поэтому  (Н×м), угловое ускорение
(Н×м), угловое ускорение  (рад/с2).
(рад/с2). и угол поворота
и угол поворота  в момент времени
в момент времени  .
. , а угол поворота — как
, а угол поворота — как  . В момент времени
. В момент времени  (с):
(с):  (рад/с);
(рад/с);  (рад).
(рад). в моменты времени
в моменты времени  . В начальный момент времени
. В начальный момент времени  (с):
(с):  (кг×м2/с); в момент времени
(кг×м2/с); в момент времени  (кг×м2/с). По основному закону динамики вращательного движения
(кг×м2/с). По основному закону динамики вращательного движения  (Н×м), что совпадает с результатом задания 1.
(Н×м), что совпадает с результатом задания 1. результирующего момента сил в интервале времени
результирующего момента сил в интервале времени  по формуле механической работы.
по формуле механической работы. . В данном случае
. В данном случае  (Н×м), угол поворота за время
(Н×м), угол поворота за время  (с) составляет
(с) составляет  (рад), получаем
(рад), получаем  (Дж).
(Дж). и
и  в моменты времени
в моменты времени  и
и  .
. В момент времени
В момент времени  (Дж), в момент времени
(Дж), в момент времени 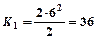 (Дж).
(Дж).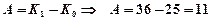 (Дж), что совпадает с результатом здания 4.
(Дж), что совпадает с результатом здания 4.


