
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа. Энергия. Закон сохранения энергии в механике
Работа. Рассмотрим малое перемещение В механике вводится понятие элементарной работы силы
α – угол между векторами
Работа силы
Данное выражение справедливо не только для материальной точки, но и вообще для любого тела или системы тел. В этом случае под
Работу Элементарную работу можно также представить как
а в декартовых координатах
Сила
Примеры вычисления работы: 1) работа упругой силы
2) работа гравитационной силы
Если на тело в процессе движения действует несколько сил, результирующая которых
Единицей работы в СИ является джоуль (Дж). Мощность – это работа, совершаемая силой за единицу времени (т.е. скорость, с которой совершается работа).
Зная зависимость мощности от времени, можно найти работу
Единицей мощности в СИ является ватт (Вт).
Энергией Е называется скалярная физическая величина, являющаяся общей мерой движения и взаимодействия всех видов материи. Энергия не исчезает и не возникает из ничего; она может лишь переходить из одной формы в другую (механическую, внутреннюю, электромагнитную, ядерную и др.).
Кинетической энергией К механической системы называется энергия механического движения этой системы. Изменение кинетической энергии материальной точки происходит под действием приложенной к ней силы
Закон изменения кинетической энергии: приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все части системы
Значения скорости и кинетической энергии одной и той же материальной точки различны в двух системах отсчёта, движущихся друг относительно друга. Рассмотрим инерциальную систему отсчёта К и систему К*, движущуюся относительно К поступательно со скоростью Для каждой материальной точки Тогда
Для кинетической энергии системы
Здесь т – масса всей системы;
Если в качестве К* -системы взять Ц -систему (систему центра масс), то Получаем теорему Кёнига:
кинетическая энергия механической системы равна сумме кинетической энергии той же системы в её движении относительно Ц -системы и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью её центра масс. Из теоремы Кёнига следует, что кинетическая энергия твёрдого тела равна сумме его кинетической энергии в поступательном движении со скоростью центра масс тела (центра инерции) и кинетической энергии вращения этого тела вокруг центра масс..
Если твёрдое тело вращается вокруг неподвижной точки О с угловой скоростью
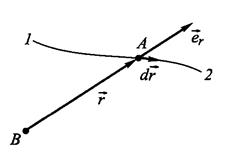
Консервативные силы Силу, действующую на материальную точку, называют консервативной или потенциальной, если работа этой силы зависит только от начального и конечного положения материальной точки. Работа консервативной силы не зависит ни от вида траектории точки между её начальным (1) и конечным (2) положениями, ни от закона движения точки по траектории
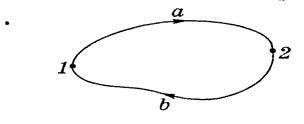
Работа консервативной силы на произвольной замкнутой траектории l точки её приложения равна нулю
Существуют силы, которые не принято называть консервативными, хотя они и удовлетворяют условиям для консервативных сил. Это силы, зависящие от скоростей материальных точек и направленные перпендикулярно этим скоростям. Работа таких сил, часто называемых гироскопическими силами, всегда равна нулю независимо от того, как движутся материальные точки, к которым они приложены. Например, сила Лоренца, действующая со стороны магнитного поля на движущуюся в нём заряженную частицу.
К числу неконсервативных сил относятся, например, силы трения и сопротивления движению в какой-либо среде. Работа этих сил зависит от пути между начальным и конечным положениями частицы (и не равна нулю на любом замкнутом пути).
Потенциальная энергия
Работа А 1-2, совершаемая консервативными (потенциальными) силами при изменении конфигурации системы, т.е. расположения её частей (материальных точек) относительно системы отсчёта, не зависит от того, как конкретно осуществляется процесс перехода из начальной конфигурации системы (1) в конечную (2). Работа А 1-2 полностью определяется начальной и конечной конфигурациями системы. Следовательно, её можно представить в виде разности значений некоторой функции конфигурации системы W, называемой потенциальной энергией системы: A 1-2 = W 1 – W 2.
Элементарная работа потенциальных сил при малом изменении конфигурации системы:
Потенциальную энергию системы можно найти только с точностью до произвольного постоянного слагаемого. В каждой конкретной задаче для получения однозначной зависимости W от конфигурации системы выбирают нулевую конфигурацию, в которой потенциальную энергию системы полагают равной нулю. Таким образом, потенциальной энергией механической системы называется величина, равная работе, которую совершают все действующие на систему консервативные силы при переводе системы из рассматриваемого состояния в состояние, соответствующее её нулевой конфигурации. Рассмотрим простейшую механическую систему, состоящую из одной материальной точки, на которую действует консервативная сила
Откуда следует:
Вектор, стоящий в скобках и построенный с помощью скалярной функции W называется градиентом функции W и обозначается Итак
Пример 1. Потенциальная энергия материальной точки в однородном поле силы тяжести.
h – высота подъёма тела над поверхностью Земли; W0 = 0 на поверхности Земли.
Пример 2. Потенциальная энергия упруго деформируемого тела.
Пример 3. Потенциальная энергия материальной точки в поле центральных сил. Силы, действующие на материальную точку, называются центральными, если они зависят только от расстояния между материальной точкой и некоторой неподвижной точкой – центром силы – и направлены всюду от центра силы либо всюду к центру силы. Если центр силы принять за начало координат, то центральная сила
Для сил отталкивания Для сил притяжения Докажем, что поле центральных сил потенциально:
Найдём потенциальную энергию материальной точки:
Обычно полагают, что
а ) для гравитационного поля материальной точки или однородного шара М – масса материальной точки или однородного шара, создающих гравитационное поле; т – масса материальной точки, находящейся в рассматриваемом поле.
б) для электростатического поля точечного электрического заряда или равномерно заряженных шара или сферы
Механической энергией системы называют величину Е, равную сумме кинетической и потенциальной энергий системы:
E = K + W. Изменение механической энергии системы равно алгебраической сумме работ всех неконсервативных сил, действующих на систему, и изменения потенциальной энергии системы за рассматриваемый промежуток времени, обусловленного нестационарностью внешних консервативных сил
Если система замкнута то
Закон сохранения механической энергии: механическая энергия замкнутой системы не изменяется, если все внутренние силы консервативные (потенциальные) либо не совершают работы (например, силы трения покоя и гироскопические силы работы не совершают).
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.22.250 (0.064 с.) |
 , в пределах которого силу
, в пределах которого силу  , действующую на материальную точку, можно считать постоянной.
, действующую на материальную точку, можно считать постоянной.

 , где
, где – элементарный путь;
– элементарный путь;
 – проекция вектора
– проекция вектора  на вектор
на вектор  на всём участке 1-2 определяется интегрированием
на всём участке 1-2 определяется интегрированием .
. следует понимать перемещение точки приложения силы.
следует понимать перемещение точки приложения силы.
 геометрически можно найти как площадь фигуры, ограниченной кривой
геометрически можно найти как площадь фигуры, ограниченной кривой  , ординатами 1 и 2 и осью
, ординатами 1 и 2 и осью  . При этом площадь фигуры над осью
. При этом площадь фигуры над осью  – со знаком «–».
– со знаком «–». ,
,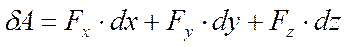 .
. в общем случае – функция нескольких переменных, а элементарная работа силы
в общем случае – функция нескольких переменных, а элементарная работа силы  не является, вообще говоря, полным дифференциалом какой либо функции координат точки. Поэтому принято элементарную работу обозначать символом
не является, вообще говоря, полным дифференциалом какой либо функции координат точки. Поэтому принято элементарную работу обозначать символом  , а не
, а не  .
. , где
, где  – радиус-вектор точки приложения силы относительно точки О.
– радиус-вектор точки приложения силы относительно точки О.
 – проекция вектора
– проекция вектора 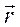 .
. .
.

 .
. 3) работа однородной силы тяжести
3) работа однородной силы тяжести  , где
, где  – орт вертикальной оси Z, положительное направление которой выбрано вверх.
– орт вертикальной оси Z, положительное направление которой выбрано вверх.
 .
. , то работа результирующей силы
, то работа результирующей силы  на некотором перемещении равна алгебраической сумме работ, совершаемых каждой из сил в отдельности на том же перемещении.
на некотором перемещении равна алгебраической сумме работ, совершаемых каждой из сил в отдельности на том же перемещении. .
. .
. .
. и равно работе, совершаемой этой силой:
и равно работе, совершаемой этой силой:
 .
. .
. .
. .
. .
.
 и К* – значения импульса и кинетической энергии рассматриваемой системы в системе отсчёта К*.
и К* – значения импульса и кинетической энергии рассматриваемой системы в системе отсчёта К*. и р*= 0 т.к. любая система частиц как целое покоится в своей Ц -системе
и р*= 0 т.к. любая система частиц как целое покоится в своей Ц -системе  .
.
 , где
, где и
и  - момент инерции твёрдого тела и его угловая скорость вращения относительно мгновенной оси, проходящей через центр масс.
- момент инерции твёрдого тела и его угловая скорость вращения относительно мгновенной оси, проходящей через центр масс. , то его кинетическая энергия
, то его кинетическая энергия , где
, где – момент импульса тела относительно точки О, принятой за начало координат;
– момент импульса тела относительно точки О, принятой за начало координат; – момент инерции твёрдого тела относительно оси, проходящей через точку О и параллельной вектору
– момент инерции твёрдого тела относительно оси, проходящей через точку О и параллельной вектору  .
.
 .
. .
.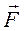
 или
или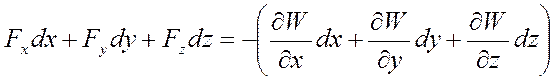
 или
или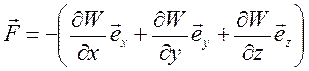 .
. .
.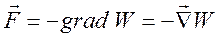 , где
, где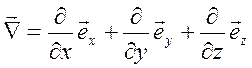 – оператор набла.
– оператор набла.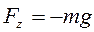 ;
;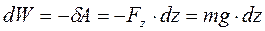
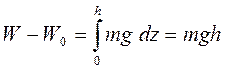 .
.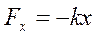 по закону Гука;
по закону Гука;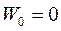 при х = 0 (для недеформированного тела);
при х = 0 (для недеформированного тела);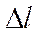 – деформация (удлинение или сжатие деформируемого тела).
– деформация (удлинение или сжатие деформируемого тела).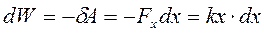
 .
.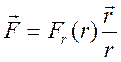 , где
, где – радиус вектор, проведённый из центра силы в рассматриваемую точку поля;
– радиус вектор, проведённый из центра силы в рассматриваемую точку поля; – расстояние от точки до центра силы;
– расстояние от точки до центра силы;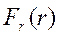 – проекция силы
– проекция силы  на радиус-вектор
на радиус-вектор  ;
; .
. т.к.
т.к. 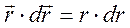 и
и .
. .
.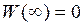 . Тогда
. Тогда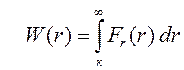 .
. , где
, где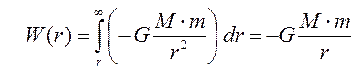 .
.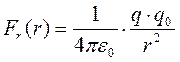 .
. .
. .
.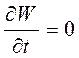 .
.


