
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комментарии к законам НьютонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сила инерции Законы Ньютона справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона:, где - это ускорение, наблюдаемое в рассматриваемой системе отсчёта, и - ускорение данной точки этой неинерциальной системы отсчёта относительно любой инерциальной системы отсчёта. Однако часто, для упрощения рассмотрения, вводят фиктивную «силу инерции», и тогда эти уравнения движения переписываются в виде, идентичном второму закону Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального воздействия на тело. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличается движение в инерциальной и неинерциальной системах отсчета. Законы Ньютона и Лагранжева механика Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), и из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами). Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима. Решение уравнений движения Уравнение является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию(перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости. Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
3. Вращением твёрдого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения. При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.
Положение плоскости Положение тела относительно выбранной системы отсчета однозначно определяется в любой момент времени, если задано уравнение
Рис. 4-4
У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла Угол Для характеристики вращательного движения твердого тела вокруг неподвижной оси введём понятия угловой скорости и углового ускорения. Алгебраической угловой скоростью тела в какой-либо момент времени называется первая производная по времени от угла поворота в этот момент, то есть Угловая скорость является положительной величиной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает. Размерность угловой скорости по определению: В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернётся на угол
Алгебраическим угловым ускорением тела называется первая производная по времени от угловой скорости, то есть вторая производная от угла поворота т.е. Размерность углового ускорения по определению: Введем понятия векторов угловой скорости и углового ускорения тела.
Рис. 4-5
Если
ВРАЩАЮЩИЙ МОМЕНТ - мера внеш. воздействия на вращающееся тело, изменяющего угл. скорость вращения. В. м. равен алгебраич. сумме моментов всех действующих на вращающееся тело сил относительно оси вращения (см. Момент силы).В. м. может быть также выражен через угл. ускорение тела Результаты выполненных экспериментов можно записать в виде:
Это основное уравнение динамики вращательного движения тела: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично по форме записи выражению второго закона Ньютона для поступательного движения тела. Ускорению поступательного движения тела а соответствует угловое ускорение вращательного движения
4. Слово «энергия» в переводе с греческого означает «действие». Энергичным мы называем человека, который активно двигается, производя при этом множество разнообразных действий. Энергия в физике И если в жизни энергию человека мы можем оценивать в основном по последствиям его деятельности, то в физике энергию можно измерять и изучать множеством различных способов. Ваш бодрый друг или сосед, скорее всего, откажется повторить тридцать-пятьдесят раз одно и то же действие, когда вдруг вам взбредет на ум исследовать феномен его энергичности. А вот в физике вы можете повторять почти любые опыты сколь угодно много раз, производя необходимые вам исследования. Так и с изучением энергии. Ученые-исследователи изучили и обозначили множество видов энергии в физике. Это электрическая, магнитная, атомная энергия и так далее. Но сейчас мы поговорим о механической энергии. А конкретнее о кинетической и потенциальной энергии.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.007 с.) |

 Пусть точки A и B неподвижны. Вдоль оси вращения направим ось
Пусть точки A и B неподвижны. Вдоль оси вращения направим ось 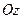 . Через ось вращения проведём неподвижную плоскость
. Через ось вращения проведём неподвижную плоскость 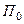 и подвижную
и подвижную 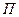 , скреплённую с вращающимся телом (при
, скреплённую с вращающимся телом (при 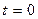
 ).
). . Угол
. Угол 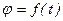 , где
, где 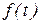 - любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси.
- любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси. .
.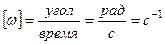
 , где n - число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим
, где n - число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим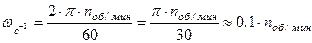

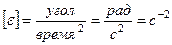
 и
и  , где
, где 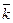 - единичный вектор оси вращения. Векторы
- единичный вектор оси вращения. Векторы 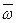 и
и 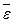 можно изображать в любых точках оси вращения, они являются скользящими векторами.
можно изображать в любых точках оси вращения, они являются скользящими векторами.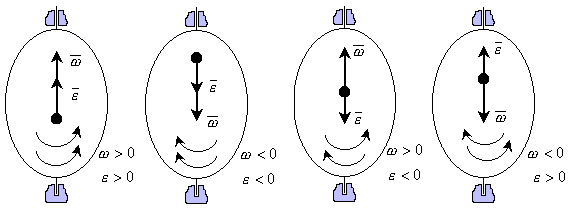
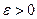 при
при 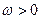 , то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов
, то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов  .
.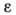 равенством
равенством 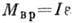 , где I - момент инерции тела относительно оси вращения.
, где I - момент инерции тела относительно оси вращения. (2.1)
(2.1)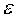 . Аналогом силы F при поступательном движении, является момент силы М во вращательном движении, а аналогом массы тела m при поступательном движении, служит момент инерции тела I при вращательном движении.
. Аналогом силы F при поступательном движении, является момент силы М во вращательном движении, а аналогом массы тела m при поступательном движении, служит момент инерции тела I при вращательном движении.


