
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы динамики (Ньютон, 1687г.)Содержание книги
Поиск на нашем сайте
I закон Ньютона (закон инерции). Всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.[3] Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инерцией. Количественной мерой инерции или инертности тела (или материи в любом ее виде) является его масса m (инертная масса). Существует также и гравитационная масса, определяющая гравитационные свойства физических тел. Сейчас экспериментально доказано (с точностью ~ 10−12), что инертная и гравитационная массы равны друг другу, поэтому в дальнейшем мы не будем их разграничивать (о другом проявлении массы поговорим в 2.8). Системы отсчета, в которых выполняется I закон Ньютона, называются инерциальными. Таким образом, I закон Ньютона утверждает существование инерциальных систем отсчета. Все инерциальные системы отсчета равноправны: механические явления в них протекают одинаково и законы движения (и не только законы движения) для всех таких систем отсчета имеют одинаковую форму. А это означает, что никакими механическими опытами внутри данной инерциальной системы отсчета нельзя установить, покоится ли она или движется с Система отсчета, движущаяся с ускорением относительно инерциальных систем, является неинерциальной (пример: лифт, движущийся с ускорением). За счет взаимодействия с другими телами тело приобретает ускорение Сила ( Сила наглядно обозначается стрелкой и, как векторная величина, характеризуется величиной (модуль вектора = длина стрелки), направлением и точкой приложения.
II закон Ньютона. Ускорение, приобретаемое материальной точкой (телом) пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
Импульс тела (количества движения)
В классической механике считается, что масса тела не зависит от скорости (
Единица силы (Ньютон) в СИ определяется из II закона Ньютона: 1Ньютон (1Н) = (1кг 1м / 1с2). 1 Ньютон − это такая сила, которая сообщает массе 1кг ускорение 1м/с2 в направлении действия силы. Выражение (3) называется также уравнением движения материальной точки. Фактически I закон динамики вытекает из II закона динамики (при
Отсюда: Согласно принципу независимости действия сил, ускорения и силы можно разлагать на составляющие:
III закон Ньютона. Силы, с которыми действуют друг на друга тела, равны по модулю и противоположены по направлению.
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы. III закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Механическая система – совокупность материальных точек (тел), которая рассматривается как единое целое. Центром масс (центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы и радиус-вектор
где mi и ri -соответственно масса и радиус-вектор i - й материальной точки; n - число материальных точек в системе, Для двух точечных масс m1 и m2, местоположение центра масс определяется соотношением m1ℓ1=m2ℓ2 (рис.14).
Импульс системы равен произведению массы системы m на скорость 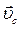 ее центр масс. ее центр масс. 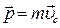
Закон движения центра масс системы Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которой действует равнодействующая внешних сил. Движение Земли и Луны, Земли вокруг Солнца, двойных звезд, движение лодки и человека, пригнувший с лодки.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 961; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.173.134 (0.011 с.) |

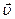 =const (принцип относительности Галилея – Ньютона (1636г)). 1905г. Эйнштейн обобщил этот принцип и для явлений любой природы. Примером инерциальной системы отсчета можно считать гелиоцентрическую (звездную) систему отсчета. По меньшей мере, инерциальной можно считать систему отсчета, связанную с Землей (хотя она вращается вокруг своей оси и вокруг Солнца, но эти центростремительные ускорения очень малы − 0,03м/с2 и 0,001м/с2 соответственно).
=const (принцип относительности Галилея – Ньютона (1636г)). 1905г. Эйнштейн обобщил этот принцип и для явлений любой природы. Примером инерциальной системы отсчета можно считать гелиоцентрическую (звездную) систему отсчета. По меньшей мере, инерциальной можно считать систему отсчета, связанную с Землей (хотя она вращается вокруг своей оси и вокруг Солнца, но эти центростремительные ускорения очень малы − 0,03м/с2 и 0,001м/с2 соответственно). . Количественной мерой взаимодействия тел является сила.
. Количественной мерой взаимодействия тел является сила. ) – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
) – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.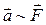 (при m=const) и
(при m=const) и 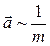 (при
(при 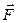 = const), тогда
= const), тогда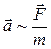 →
→ 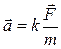 . В системе СИ k=1
. В системе СИ k=1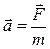 или
или 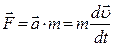 (1)
(1)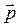 – это произведение массы тела
– это произведение массы тела 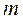 на скорость его движения
на скорость его движения 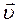 .
.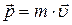 (2)
(2)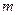 = const). Поэтому дифференциальная форма II закона Ньютона формулируется как− скорость (быстрота) изменения импульса тела определяется действующей на это тело внешней силой (определение Ньютона):
= const). Поэтому дифференциальная форма II закона Ньютона формулируется как− скорость (быстрота) изменения импульса тела определяется действующей на это тело внешней силой (определение Ньютона):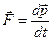 . (3)
. (3)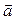 тоже равняется нулю), но из-за важности (I закон утверждает существование инерциальных систем отсчета, в которых выполняется II закон) он остается как самостоятельный закон.
тоже равняется нулю), но из-за важности (I закон утверждает существование инерциальных систем отсчета, в которых выполняется II закон) он остается как самостоятельный закон.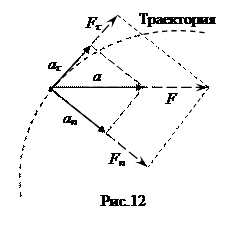 Принцип независимости действия сил: Ускорение, вызванное какой-либо одной силой, не зависит от того, действуют ли на данное тело одновременно какие-либо другие силы. Иными словами, если на тело одновременно действуют несколько сил, то равнодействующая (результирующая) сила равна векторной сумме всех приложенных к телу сил.
Принцип независимости действия сил: Ускорение, вызванное какой-либо одной силой, не зависит от того, действуют ли на данное тело одновременно какие-либо другие силы. Иными словами, если на тело одновременно действуют несколько сил, то равнодействующая (результирующая) сила равна векторной сумме всех приложенных к телу сил.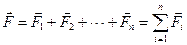
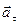 +
+  ;
; 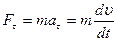 ,
, 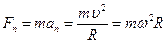 .
.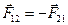
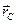 которой определяется выражением (рис.13):
которой определяется выражением (рис.13):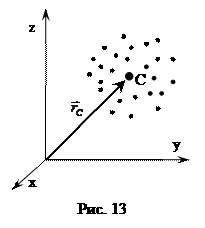
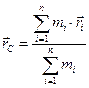 , (4)
, (4)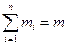 общая масса системы. Центр масс можно считать точкой, в которой сосредоточена масса системы или тела при его поступательном движении.
общая масса системы. Центр масс можно считать точкой, в которой сосредоточена масса системы или тела при его поступательном движении.
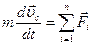 .
.


