
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аберрации или погрешности оптических системСодержание книги
Поиск на нашем сайте
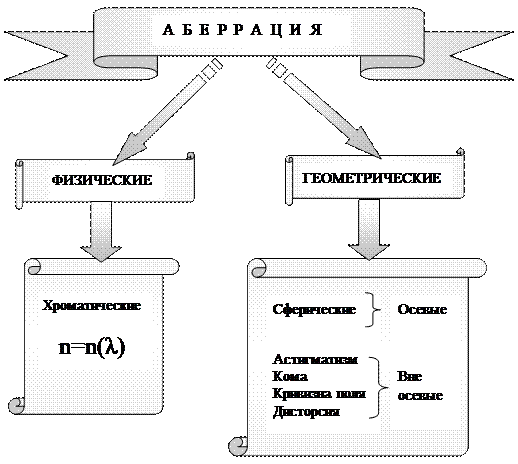
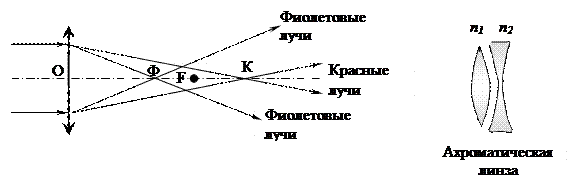
Хроматическая аберрация возникает из-за того, что коэффициент преломления n=n(λ) зависит от длины волны света (явление дисперсии − отсутствует у зеркал). Собирающая линза приближает к оптической оси сильнее фиолетовые лучи, чем красные, а рассеивающая линза, наоборот, приближает к оптической оси сильнее красные лучи. Благодаря этому можно создать оптическую систему (ахроматическая линза), не имеющую хроматической аберрации. Комбинация двух линз с разными п уменьшает хроматическую аберрацию много (~16) раз. Так как разные сорта стекол обладают различной дисперсией, то, комбинируя собирающие и рассеивающие линзы из различных стекол, можно совместить фокусы двух (ахроматы) и трех (апохроматы) различных цветов, устранив тем самым хроматическую аберрацию. Системы, исправленные на сферическую и хроматическую аберрации, называются аплантами. Хроматическую аберрацию можно уменьшить, увеличивая фокусное расстояние линзы, хотя это не всегда технически выполнимо. Например, при диаметре линзы D=0,5м, F=2,8м, при D=1м, F=112м (технически невыполним). Сферическая аберрация обусловлена сферичностью преломляющих поверхностей линз (отсутствует у параболических зеркал). При большом диаметре линзы часть лучей перестанут быть параксиальными, в результате чего изображения получаются размытыми (сферическая аберрация).
У собирающей линзы лучи, падающие на ее края, собираются ближе, чем лучи, падающие на ее центральную часть (δ<0); у рассеивающей линзы наблюдается обратное явление (δ>0). Благодаря этому можно создать оптическую систему (анастигматы) из соответствующим образом подобранных собирающей и рассеивающей линз, у которой сферическая аберрация почти полностью отсутствует. Применяя диафрагмы (ограничиваясь параксиальными лучами), можно уменьшить сферическую аберрацию, однако пи этом уменьшается светосила линзы. В 1941г. Д.Д. Максутовым была создана безаберрационная оптическая система (менисковый телеобъектив), состоящая из вогнутого сферического зеркала и выпукло-вогнутой сферической линзы (мениска). Зеркало и мениск в отдельности обладают большими аберрациями (сферическими), имеющими противоположные знаки; в менисковом телеобъективе эти аберрации полностью компенсируются.
Сферическая аберрация является частным случаем астигматизма. Астигматизм − погрешность, обусловленная неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка. Устраняется при помощи сложных линз (широкоугольные объективы до 700). Астигматизм исправляется подбором радиусов кривизны преломляющих поверхностей и их фокусных расстояний. Системы, исправленные на сферическую и хроматическую аберрации и астигматизм, называются анастигматами.
Просветленная оптика Для уменьшении отражения на границах линз, их покрывают пленкой фторида магния MgF2 с
Примеры по геометрической оптике:
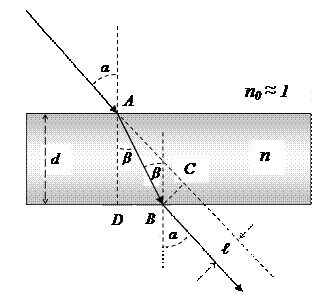
Приложение 1 Прохождение света через плоскопараллельную пластину Пластина смещает луч света параллельно самому себе на расстояние ℓ
Из ΔABC → BC=AB.sin(α─β) Из ΔADB → AB=d/cosβ BC=ℓ=d.sin(α─β)/cosβ Или как f(d,α,n)
Приложение 2 Формула тонкой линзы (по Физика для поступающих, Бутиков Е.И. и др.,М., «Наука», 1978г.)
a+n(c+d)+b=AC+CB Из теоремы Пифагора:
= Т.к. h<<d, то используя Аналогично поэтому также c= Окончательно Приложение 3 Формула тонкой линзы (по Трофимовой)
Две световые лучи, выходящие из точки А (луч АОВ и луч, проходящий через край линзы, АСВ), должны доходить до точки В, одновременно. Время прохождения света вдоль АОВ  , где N=n/n1 -относительный показатель преломления (n и n1 - соответственно абсолютные показатели преломления линзы и окружающей среды). Время прохождения света вдоль АСВ равно , где N=n/n1 -относительный показатель преломления (n и n1 - соответственно абсолютные показатели преломления линзы и окружающей среды). Время прохождения света вдоль АСВ равно  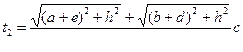 . Так как t1=t2, то . Так как t1=t2, то  . .
Рассматривается параксиальные (приосевые) лучи, т. к. только они, исходящие из точки A, пересекают оптическую ось в одной и той же точке В. тогда h<<(a+e), h<<(b+d) и
Для тонкой линзы e<<a и d<<b, поэтому Приложение 4 Формула тонкой линзы (по Грабовскому)
Построим плоскости, касательные к поверхностям линзы в точках M и N (т.е. в местах падения луча на линзу и выхода его из линзы), и проведем в эти точки радиусы R1 и R2 кривизны линзы. Тогда луч AMNA1 можно рассматривать как луч, преломленный в тонкой призме с преломляющим углом θ. Учитывая малость углов α, β, α1, β1 и толщины линзы, можно написать следующие приближенные равенства: h1≈h2, |AD|≈a,|A1D1|≈b,
где h1 - высота (над оптической осью) точки M падения луча на линзу, h2 - высота точки N выхода луча из линзы, a и b - соответственно расстояния от источника света A и от его изображения A1 до оптического центра линзы. Из треугольников AHA1 и BEB 1 следует, что δ=α+α1 и θ=β+β1. Тогда, принимая во внимание значения α, α1, β, β1, получим
Но, согласно формуле призмы δ=(n−1)θ, где n - абсолютный показатель преломления линзы. Поэтому
В эту формулу тонкой линзы не входит высота h1. Это означает, что расстояние b не зависит от местоположения точки M, т.е. все лучи, исходящие из точки А, соберутся после преломления различными частями линзы в одной точке А1. §2. ВОЛНОВАЯ ОПТИКА
Волновой оптикой называется раздел оптики, где свет рассматривается как часть электромагнитных волн и изучаются классические законы излучения, распространения и взаимодействия световых волн с веществом.
§2.1. Интерференция света
Явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других, называется интерференцией волн. Необходимым условием интерференции волн является их когерентность, т.е. некая согласованность между ними. Когерентные волны – это такие волны, у которых в данной точке пространства разность фаз не меняется в течении времени: Δ (получается из формулы волны − Независимость разность фаз от времени означает, что когерентными могут быть лишь волны, имеющие одинаковую частоту (длину волны). Интерференционная картина, т.е. взаимное усиление когерентных волн в одних точках пространства и ослабление в других, получится только в том случае, если когерентные волны в данной точке пространства встречаются всегда одинаковым образом. Например, если в данной точке пространства они всегда встречаются в одинаковой фазе, то мы наблюдаем усиление волн (интерференционные максимумы). Если же они встречаются в противофазе, то гасят друг друга, и мы наблюдаем ослабление волн (интерференционные минимумы). При сложении двух когерентных волн (для простоты амплитуды гармонических колебаний принимаются одинаковым); s1 =A cos (ωt + φ1) s2 =A cos (ωt + φ2). По принципу суперпозиции их сложение s=s1+ s2= 2A cos (ωt + где Aрезулт. =2A cos( (если гармонические колебания выражаются через sin, товместе cos (ωt + Так как
Тогда Aрезулт принимает максимальное значение в точках 2kπ:
Таким образом, условия максимумов имеет вид
поэтому условия минимумов: Для общего случая:
A2=A12+A22+2A1A2 cos (φ1–φ2) Так как I=A2, то I=I1+I2+2 Для когерентных волн cos (φ1–φ2)=const; не зависит от времени, но для каждой точки пространства имеет свое значение. Когда cos (φ1–φ2)>0, то I>I1 +I2; при cos (φ1–φ2)<0, I<I1 +I2 Следует отметить, что при интерференции волн не происходит простое сложения их энергий. При I1 =I2, в максимуме I=4I1, а в минимуме I=0. Например, в точках минимума или около них энергия волн, дошедших от двух источников меньше, чем энергия волны одного источника. Интерференция волн приводит к перераспределению энергии колебаний между различными близкорасположенными частицами среды. В среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн. У некогерентных волн в среднем cos (φ1–φ2)=0 и при I1 =I2; I=2I1. Таким образом, если когерентные волны в точку А приходят из двух источников S1 и S2, то условия максимума и минимума для них имеет вид:
где Δ – разность хода лучей, k = 0, 1, 2,… Иными словами, если в разность хода лучей умещается четное количество полуволн (или целое число волны), то в этой точке мы имеем максимальное усиление волны. Если же в разность хода лучей помещается нечетное количество полуволн, то в этих точках происходить ослабление волн.
Следует отметить, что когерентность волн в течении времени и при больших значениях разности хода нарушаются. При отражении света в разность хода Δ появляется дополнительная разность фаз; если свет отражается от границы с оптически более плотной среды (зеркало), то фаза колебания светового вектора скачками меняется на π («потеря полуволны» при отражении). В этом случае к Δ надо прибавить или отнять λ/2. Линзы дополнительной разности хода не вносят. Так как свет, исходящий из светящегося тела, представляет собой совокупность множества электромагнитных волн, излучаемых отдельными частицами (атомами и молекулами) тела, то световые волны от независимых источников практически не могут быть когерентными (исключение составляют лазеры). Для получения интерференционной картины (когерентных световых волн) применяют метод «разделения» волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга. Такое «раздвоение» можно осуществить, например, посредством экрана с двумя малыми отверстиями, которые играют роль независимых источников (метод Юнга), отражением света от двух плоских зеркал, установленных под углом ~1800 (зеркало Френеля) или прохождением света через два одинаковых, сложенных основаниями призм с малыми преломляющими углами (бипризма Френеля).
Интерференция света в тонких пленках В условиях максимумов и минимумов разность хода зависит от длины волны. Это приводит к тому, что для белого света, который представляет собой смесь различных цветов (различных λ), светлые полосы в интерференционных картинах приобретают радужную окраску. В природе это наблюдается в тонких пленках, которые образуют, например, мыльные пузыри или масляные пленки на воде или на асфальте. В данном случае, интерференция происходит между двумя волнами (I и II), отраженными от двух (верхних и нижних) поверхностей пленки.
Δ=(|AD|+|DC|)−(|AB|±λ/2) член λ/2 из-за эффекта полуволн Если n>n0, то потеря полуволны произойдет в точке А и вышеупомянутый член будет иметь отрицательный знак (−); если же n<n0, то потеря полуволны произойдет в точке D и λ/2 будет иметь знак (+) |AD|=|DC|=h/cosr |AB|=|AC|sini=2h.tgr.sini Учитывая, что sin2r=1–cos2r и sini=n .sinr, получаем Δ=2nh cosr+λ/2 Δ= Разность хода Δ зависит от толщины пленки (h), коэффициента преломления вещества (n), из чего состоит пленка, от угла падения (i) и длины волны света (λ). При больших значениях h когерентность I и II волн нарушается, поэтому интерференция наблюдается у тонких пленок.
Полосы равной толщины (интерференция от пластинки переменной толщины) наблюдается, когда параллельный пучок (i=const) монохроматического света (λ=const) падает на однородную (n=const) пластину, толщина которой меняется от точки к точке (h≠const). Полосы равного наклона (интерференция от плоскопараллельной пластины) получается при h=const. n=const, λ=const, но при i≠const. 1′,1′′,2′ и 2′′ параллельны (так как пластинка параллельна), поэтому, чтобы их наблюдать используют собирающую линзу, при помощи которой они на экране собираются в точке F. Лучи, подающие под другим углом (3) собираются в другой точке F′. Если оптическая ось линзы перпендикулярна поверхности пластинки, то получаются концентрические кольца с центром в фокусе линзы.
Кольца Ньютона наблюдаются при отражении света от воздушного зазора (ЕС), образованного плоскопараллельной пластинкой (П) и соприкасающейся с ней плосковыпуклой линзой (Л) с большим радиусом (R) кривизны и являются частным случаем интерференционных полос равной толщины.
Параллельный пучок монохроматического света падает нормально на плоскую поверхность АВ линзы и частично отражается на границах раздела сред. Рассмотрим ход луча, падающего в точку А плоской поверхности линзы. Отражение волн происходит в точках А, С, Е и F. Оптическая разность хода между волнами, отраженными в точках А и С (а также в точках А и Е, С и F), значительно превышает длину когерентности электромагнитных волн, испускаемых лампой. Достаточно малую разность хода имеют только волны, отраженные от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой, в точках С и Е (радиус R линзы выбирают весьма большим, поэтому эти волны можно считать когерентными). Попадая в глаз наблюдателя, эти волны и обусловливают интерференционную картину.
Вследствие симметрии интерференционная картина имеет вид чередующихся светлых и темных концентрических колец, ширина и интенсивность которых постепенно убывает по мере удаления от центра картины (правый рисунок, б). В центре картины, где Из левого рисунка видно, что Δ= Также видно, что R2=(R−d)2+r2, где r - радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Так как d<<R, то d=r2/2R и Из условия максимума Δ=± mλ0 (m=0,1,2,…) Для радиусов m -го светлого кольца получаем:
Связь между радиусом m темного интерференционного кольца
Но для экспериментальной проверки эта формула не применима т.к. в действительности между линзой и пластиной в точке О всегда имеется незначительный зазор. Чтобы исключить искажения, вносимой этим зазором, возведем формулу Отсюда
Эта формула уже может быть применена и в том случае, когда стеклянная линза не плотно примыкает к плоскопараллельной пластинке вследствие попадания пыли.
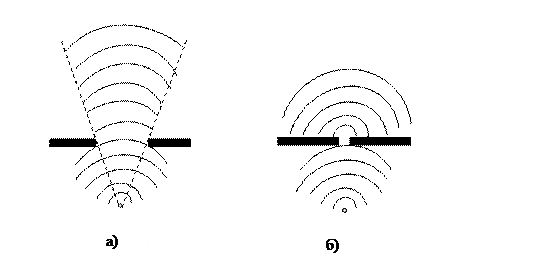
Дифракция света Явление непрямолинейной распространения света вблизи преграды (огибание световым лучом преграды и проникновение света в область геометрической тени) называется дифракцией света, а получающаяся картина – дифракционной, т.е. дифракция, в более широком смысле, - это любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Огибание препятствий звуковыми волнами (т. е. дифракция звуковых волн) наблюдается повсеместно постоянно в обыденной жизни. Для наблюдения дифракции световых волн необходимо создание специальных условий, так как их длина волны гораздо меньше, чем у звуковых волн. На рисунке схематично показаны дифракции механических волн на поверхности воды. Путь волнам на поверхности воды преграждает экран с щелью, от ширины которой зависит картина распространения волн. Если размеры щели велики по сравнению с длиной волны (левый рисунок, а)), то волна проходит сквозь щель, почти не меняя своей формы (только по краям можно заметить небольшие искривления волновой поверхности). Если же размеры щели соизмеримы или меньше чем длина волны, то за экраном распространяется круговая волна, как если бы источник волны располагался в отверстии экрана (правый рисунок, б)).
Таким образом, в данном примере, явление дифракции наблюдается в тех случаях, когда размеры препятствия малы или соизмеримы с длиной волны (отверстия в непрозрачных экранах, границы непрозрачных тел, и т. д.). Но сравнимость размеров преграды с длиной волны (например, света), не является необходимым условием для наблюдения дифракционных явлений. Если дифракционная картина наблюдается на достаточно больших расстояниях от преград, то размеры последних могут существенно превосходить длину волны. Просто, при прочих равных условиях, чем меньше длина волны и чем больше размер препятствия, тем в меньшей степени выявляется дифракционная картина и более применимы законы геометрической оптики. Дифракционная картина от маленького отверстия или круглого непрозрачного экрана представляет собой концентрические светлые и темные круги. Любопытно, что, если в центре дифракционной картинки от отверстия, изменяя диаметр отверстия, можно получить и светлое и темное пятно, то в центре дифракционной картинки от круглого экрана всегда получается светлое пятно (пятно Пуассона). Исторически, установление этого экспериментального факта (1818г.) сыграло решающую роль для утверждения волновой теории света. Явление дифракции объясняется принципом Гюйгенса-Френеля (1815), который представляет собой объединение принципа Гюйгенса с идеей интерференции вторичных волн. Согласно принципу Гюйгенса (1678), каждая точка фронта волны от источника S является элементарным, воображаемым источником новых, вторичных волн S1, S2 и т. д., огибающая которых определяет положения фронта волны в следующий момент времени.

Принцип Гюйгенса решает лишь геометрические задачи: позволяет найти направление распространения фронта волны, объяснить равенство углов падения и отражения при отражении света.
Таким образом, принцип Гюйгенса-Френеля подразумевает: · Каждая точка среды, до которой дошла волна, сама становится источником вторичных волн; · Вторичные волны взаимно гасятся во всех направлениях, кроме направлений исходного фронта.
Дифракционную картину от круглого непрозрачного экрана, от маленького отверстия или щели можно объяснить при помощи зон Френеля (методом зон Френеля). Для учета интерференции вторичных волн Френель предложил мысленно разбить волновой фронт в месте расположения преграды на кольцевые зоны (в случае дифракции от круглого отверстия или круглого непрозрачного экрана) или полосы-зоны в случае дифракции от щели. На рисунке показаны проекции этих зон на отверстии DD и их размеры. Размеры зон выбирают таким образом, чтобы расстояния от краев соседних зон до точки М отличались на λ/2. Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке М сферы радиусами L, L+λ/2, L+2λ/2, L+3λ/2,…, L+nλ/2, где L- расстояние экрана от отверстия. Свет от соседних зон гасят друг друга, так как разность хода у них равняется λ/2. Можно показать, что при таком разбивании зон, если n не слишком большое, площади зон Френеля одинаковы, а это означает, что построение таких зон разбивает волновую поверхность сферической волны на равновеликие зоны. Хотя явление дифракции общие для всех волновых процессов, для наблюдения дифракции света нужны особые условия; а именно L ≥ DD2/ λ. (так как для света λ<< DD, то дифракцию света можно наблюдать только на достаточно больших расстояниях L от преграды). Если в отверстии DD укладывается четное число зон (n=2k), то в точке М наблюдается интерференционный минимум (все зоны попарно гасят друг друга). Энергия света в результате интерференции перераспределяется в виде темных и светлых колец. Если подающий свет белый – эти кольца будут радужными. Когда n - нечетное, то в точке М – светло (интерференционный максимум), т.к. одна зона остается негашеной (n=2k+1). Общее количество N зон на полусфере очень велико: например, при a ≈ L ≈ 10см, для λ≈500нм, N ≈ 8 .105.
Следует отметить, что между интерференцией и дифракцией нет существенного физического различия. В обоих явлениях происходит перераспределение светового потока в результате суперпозиции волн. Но по историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией волн. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией волн. Поэтому говорят, например, об интерференционной картине от двух узких щелей и о дифракционной картине от одной щели, хотя эти картины качественно не отличаются друг от друга и представляют собой чередование светлых и темных полос.
Дифракция от одной щели (дифракция Фраунгофера) Дифракция Фраунгофера или дифракция в параллельных лучах наблюдается когда на узкую щель с шириной ВС=а перпендикулярно подает плоская параллельная волна. В этом случае зоны Френеля имеют вид узких полос, параллельных ребру В щели и накрывают всю открытую часть волновой поверхности в плоскости щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2,т.е. всего на ширине щели уместится
При φ=0 в точке М0 получается светлая полоса – центральный максимум. Разность хода крайних лучей: На рисунке m=2, и мыимеем дифракционный минимум. Для одной щели с шириной a условие дифракционных максимумов имеет вид: a·sin φ =± (2k+1)λ/2, где k=1, 2, 3, … порядок максимумов. Условие дифракционных минимумов: a·sin φ = ±2k·λ/2=±kλ. Когда a≈λ наблюдается только расплывчатый центральный максимум, а минимум первого порядка →∞ (φ=±π/2) При a>>λ видим прямолинейное распространение света: дифракционные максимумы высших порядков сужаются и приближаются к краям центрального максимума.
Величина d=a+b (сумма ширины a щели и промежутка b между щелями) называется периодом или постоянной решетки. Чтобы определить характер дифракционной картины от дифракционной решетки надо учесть не только дифракцию света на каждой из щелей, но и интерференцию пучков, приходящих в данную точку от разных щелей. Условия максимума: d·sin φ =±kλ или d·sin φ =±2mλ/2 (k =0,1,2,3,…). Оно дает положение главных максимумов и не зависит от количества щелей. В этих направлениях все световые векторы от всех щелей складываются в одинаковой фазе. Число максимумов меньше чем d/λ т.к. sin φ≤1. Очевидно, что в тех направлениях, в которых от одной щели не попадал свет, он не будет распространяться в этих направлениях и от двух, трех и других щелей, т.е. прежние (главные) минимумы интенсивности от одной щели сохраняются. Поэтому условие главных минимумов будет : a·sin α = ±2kλ/2 = ±kλ (k=1,2,3,…) Но кроме них появляются дополнительные минимумы вследствие интерференции от разных щелей. Условие таких дополнительных, добавочных минимумов: d·sin φ = ±(2k+1)λ/2 (k=0,1,2,3,…).
Поскольку амплитуда световых колебаний в максимуме ~ N, то освещенность в максимумах ~ N2. При увеличении N, координаты главных максимумов (при одинаковых d) не изменяются, сокращаются их ширины и увеличиваются их освещенность, а добавочные минимумы сливаются и дают общий слабый (темный) фон. Уменьшение d ведет к увеличению расстояния между главными максимумами. При белом свете получаем дифракционный спектр. В отличии от дисперсионного спектра в дифракционном спектре наиболее смещенным оказывается красный свет, а наименее – фиолетовый. Наиболее ярки спектры I порядка, остальные менее яркие и могут накладываться друг на друга – перекрываться Дифракция волн может происходить на любых мелких неоднородностях и частицах, например на кристаллах. Четкую дифракционную картину можно получить лишь в том случае, если период структуры кристалла d>λ, поэтому в этом случае используют рентгеновские лучи для которых это условие хорошо выполняется (для оптических лучей, т.к. d~10-8см, длина волн λ световых лучей ~1000 раз больше чем d).
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.180 (0.017 с.) |




 и с такой толщины, чтобы световые волны 1 и 2 гасили друг друга (имели противоположные фазы). Поглощение в стекле линз возрастает в ультрафиолетовой и инфракрасной части спектра, поэтому для этих лучей используют кварц или зеркало.
и с такой толщины, чтобы световые волны 1 и 2 гасили друг друга (имели противоположные фазы). Поглощение в стекле линз возрастает в ультрафиолетовой и инфракрасной части спектра, поэтому для этих лучей используют кварц или зеркало.


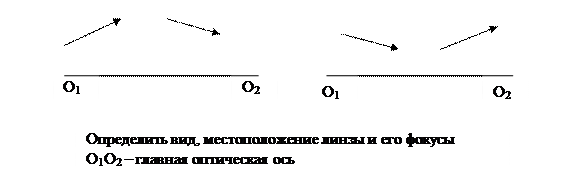
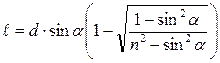
 Из принципа Ферма следует, что оптические длины всех лучей, выходящих из источника А и собирающихся в точке В, являющейся его изображением, одинаковы.
Из принципа Ферма следует, что оптические длины всех лучей, выходящих из источника А и собирающихся в точке В, являющейся его изображением, одинаковы. =
=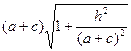
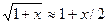 при x<<1
при x<<1 
 ,
, →
→  →
→ 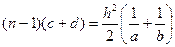 , т.к. a>>c, b>>d
, т.к. a>>c, b>>d , и аналогично
, и аналогично 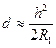 .
.

 . Аналогично
. Аналогично  .Подставив эти выражения в
.Подставив эти выражения в  .
.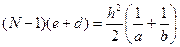 . Учитывая, что
. Учитывая, что 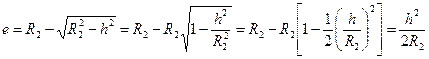 и соответственно
и соответственно  , получим
, получим 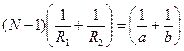

 ,
,  ,
, ,
,  ,
, и
и 
 .
. =const,
=const, ).
). ) cos(
) cos( )=Aрезулт. cos (ωt +
)=Aрезулт. cos (ωt +  и
и  , то из уравнения световой волны
, то из уравнения световой волны  выражение
выражение
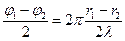 = 2kπ, где k = 0,1,2,3,…, порядок максимума
= 2kπ, где k = 0,1,2,3,…, порядок максимума
 При (2k +1)π Aрезулт имеет минимальное значение,
При (2k +1)π Aрезулт имеет минимальное значение, , где k = 0,1,2,3,…
, где k = 0,1,2,3,… ,
, 
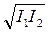 cos (φ1–φ2)
cos (φ1–φ2) , (условия максимума),
, (условия максимума), , (условия минимума),
, (условия минимума), Для световых лучей условие максимумов и минимумов относится не к разности хода лучей, а к оптической длины пути волны. Последняя собой представляет произведение геометрической длины r пути световой волны в данной среде на показатель преломления n этой среды. В общем случае, когда лучи от источников S1 и S2 приходят сквозь среды с разными показателями преломления, то Δ=|n2r2 –n1r1|. Но обычно, оба источника находятся в воздухе, для которого можно принять n1=n2=1, поэтому вместо оптической разности хода часто употребляют | r2-r1 |.
Для световых лучей условие максимумов и минимумов относится не к разности хода лучей, а к оптической длины пути волны. Последняя собой представляет произведение геометрической длины r пути световой волны в данной среде на показатель преломления n этой среды. В общем случае, когда лучи от источников S1 и S2 приходят сквозь среды с разными показателями преломления, то Δ=|n2r2 –n1r1|. Но обычно, оба источника находятся в воздухе, для которого можно принять n1=n2=1, поэтому вместо оптической разности хода часто употребляют | r2-r1 |.
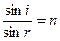
 или Δ = f (h,n,i,λ)
или Δ = f (h,n,i,λ)

 , наблюдается темное пятно (минимум нулевого порядка), что соответствует разности хода отраженных волн равной
, наблюдается темное пятно (минимум нулевого порядка), что соответствует разности хода отраженных волн равной  .
. ; такой же результат получаем из формулы Δ=
; такой же результат получаем из формулы Δ= 

 , радиусом
, радиусом  кривизны линзы и длиной световой волны
кривизны линзы и длиной световой волны 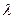 определяется соотношением
определяется соотношением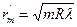 , где m=0,1,2,3…
, где m=0,1,2,3… .
.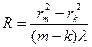 .
.

 Согласно идее Френеля, волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции (суперпозиции). А это означает, что амплитуда и фаза волны в любой точке М пространства – это результат интерференции волн, «излучаемых» множественными, вторичными, фиктивными источниками S1, S2 и т., д.
Согласно идее Френеля, волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции (суперпозиции). А это означает, что амплитуда и фаза волны в любой точке М пространства – это результат интерференции волн, «излучаемых» множественными, вторичными, фиктивными источниками S1, S2 и т., д.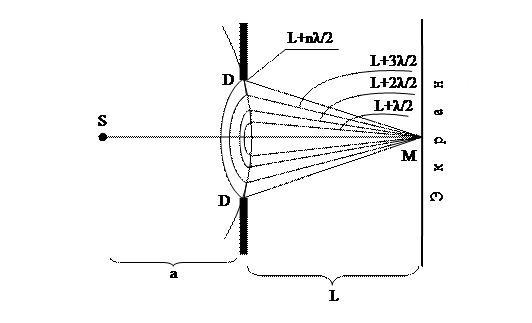
 Метод зон Френеля позволяет нам объяснить также прямолинейность распространения света. Действие всей волновой поверхности света от источника S на точку М сводится к действию ее малого участка меньшего центральной зоны. Остальные зоны друг друга гасят. Воздействия остальных зон тем меньше, чем дольше они от М и чем больше уголь φ. Амплитуда колебаний в точке М равна А ≈ А1 /2, где А1 амплитуда колебаний, возбуждаемых в точке М центральной зоной.
Метод зон Френеля позволяет нам объяснить также прямолинейность распространения света. Действие всей волновой поверхности света от источника S на точку М сводится к действию ее малого участка меньшего центральной зоны. Остальные зоны друг друга гасят. Воздействия остальных зон тем меньше, чем дольше они от М и чем больше уголь φ. Амплитуда колебаний в точке М равна А ≈ А1 /2, где А1 амплитуда колебаний, возбуждаемых в точке М центральной зоной. зон. На рисунке для простаты изображен две зоны Френеля. Чтобы получить дифракционную картину от плоской волны за щелью помещают собирающую линзу, в фокальной плоскости которой находится экран.
зон. На рисунке для простаты изображен две зоны Френеля. Чтобы получить дифракционную картину от плоской волны за щелью помещают собирающую линзу, в фокальной плоскости которой находится экран. DC=Δ=a·sin φ = mλ/2
DC=Δ=a·sin φ = mλ/2 В белом свете дифракционная картина сопровождается окраской: белый свет разлагается в спектр. Такие дифракционные спектры, получаемые при помощи дифракционных решеток, широко используются в науке и технике. Дифракционная решетка это множество параллельных, узких щелей равной ширины, разделенных непрозрачными промежутками. Они изготовляются царапанием или на стеклянную пластинку (прозрачные) или на зеркало (отражающие): количество таких щелей на 1 мм может достигать ~1500, а общее число – ~200000. Вообще говоря, роль дифракционной решетки может служить не только совокупность щелей, но и совокупность большого числа любых неоднородностей (отверстий и преград) на плоскости или в объеме. Например, окраска перламутра жемчуга объясняется дифракцией белого света на содержащихся в них мельчайших инородных вкраплениях.
В белом свете дифракционная картина сопровождается окраской: белый свет разлагается в спектр. Такие дифракционные спектры, получаемые при помощи дифракционных решеток, широко используются в науке и технике. Дифракционная решетка это множество параллельных, узких щелей равной ширины, разделенных непрозрачными промежутками. Они изготовляются царапанием или на стеклянную пластинку (прозрачные) или на зеркало (отражающие): количество таких щелей на 1 мм может достигать ~1500, а общее число – ~200000. Вообще говоря, роль дифракционной решетки может служить не только совокупность щелей, но и совокупность большого числа любых неоднородностей (отверстий и преград) на плоскости или в объеме. Например, окраска перламутра жемчуга объясняется дифракцией белого света на содержащихся в них мельчайших инородных вкраплениях.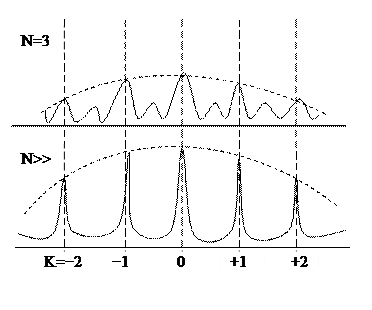 Количество минимумов зависит от количества щелей N. Между соседними главными максимумами располагаются N─1 добавочных минимумов.
Количество минимумов зависит от количества щелей N. Между соседними главными максимумами располагаются N─1 добавочных минимумов.


