
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Волновых поверхностей можно провести бесчисленное множество, а волновой фронт, также являясь волновой поверхностью, в каждый момент времени один. Волновые поверхности могут быть любой формы, но в простейшем случае они или сферические (сферическая волна) от одного точечного источника или плоские (плоская волна), когда источник волны находится очень далеко. В дальнейшем мы будем рассматривать только такие простейшие случае. Колебательные и волновые процессы весьма распространены в природе, но несмотря на их большое разнообразие, как по физической природе, так и по степени сложности, большинство из них можно описать как гармонические процессы[7]. Уравнение бегущей волны (8) в общем случае можно написать в форме: Предполагая, что фаза Продифференцировав и поделив на ω, получаем Значит υ не что иное, как скорость перемещения фазы волны (фазовая скорость). Для сферической волны (для точечных источников колебаний):
Так как A~1/r, даже если среда не поглощает энергию, то из определения волнового числа, получим υ=ω/k. Если υ в среде зависит от ω, то это явление называется дисперсией волн, а среду − диспергирующей.
2.8. Границы применимости законов классической механики и элементы специальной теории относительности Эйнштейн признавал, что он, подобно страусу «прячет голову в песок относительности, чтобы не смотреть в лицо гадким квантам…» Законы классической механики справедливы для макроскопических тел, движущихся со скоростями, гораздо меньшими, чем скорость света. Когда скорость тела близка к скорости света, применимы формулы специальной (частной) теории относительности (СТО), которую часто называют и релятивистской теорией.[8] Противоречия между классической физикой и результатами опытов (конец XIX в.). · Движение быстрых заряженных частиц не подчиняется законам классической механики; · Нарушение закона сложения скоростей; · Механика Ньютона не объяснял распространение света; · Неинвариантность уравнения Максвелла. Все эти противоречия устранял СТО, в основе, которой 2 постулата[9] Эйнштейна (1905г.) 1. Принцип относительности – никакие физические опыты (механические, электрические, оптические и др.), проведенные внутри данной инерциальной системы отсчета, не дают возможность обнаружить, покоится ли эта система или движется равномерно и прямолинейно. Все законы природы инвариантны (от слово invariant – неизменяющийся) по отношению к переходу от одной инерциальной системе отсчета к другой (обобщение механического принципа относительности Галилея − Ньютона на любые физические процессы). 2. Принцип инвариантности скорости света: Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Постоянство скорости света – фундаментальное свойство природы, которое констатируется как опытный факт (см. приложение № 4 − опыты Майкельсона − Морли). Первый постулат Эйнштейна, фактически являясь обобщением механического принципа относительности Галилея – Ньютона на любые физические процессы, утверждает, таким образом, что все физические законы инвариантны по отношению к выбору инерциальной системы отсчета, а уравнения, описывающие эти законы, одинаковы по форме во всех инерциальных системах отсчета. Для доказательства принципа относительности Галилея − Ньютона (законы динамики одинаковы во всех инерционных системах) рассмотрим две системы отсчета: инерциальную систему К (с координатами x,y,z), которую условно будем считать неподвижной, и систему К′ (с координатами x',y',z'), движущуюся относительно К равномерно и прямолинейно со скоростью В классической механике предполагается, что ход времени не зависит от относительного движения системы отсчета, т. е. t=t'. Дифференцируя x,y,z, получаем, что, ускорение точки А в системах К и К', движущихся друг относительно друга равномерно и прямолинейно, одинаково:
Но уравнения электродинамики (уравнения Максвелла) оказались неинвариантными по отношению преобразований Галилея. Поэтому, чтобы сделать уравнения Максвелла инвариантными, Лоренц (1904) вместо преобразования Галилея предлагал свои, которые при
Таблица 3 Преобразования Галилея и Лоренца
Из преобразований Лоренца следует, что и расстояние, и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках преобразований Галилея эти величины считались абсолютными, не меняющимися при переходе от одной системы к другой. Иными словами, и расстояние, и промежуток времени (заодно и одновременность события в разных инерционных системах) являются относительными величинами. Кроме того, как пространственные, так и временные преобразования не являются независимыми, поскольку в их формулы входят и время, и координаты (т.е. мы имеем четырёхмерное пространство-время). Преобразования Лоренца отражают и существенное отличие от классической механики – это наличие множителя Например, масса движущейся со скоростью Релятивистский импульс Из постулатов СТО вытекает ряд важнейших следствий, касающихся свойств пространства и времени. Например, для выражения длины при переходе от неподвижной системы к движущейся со скоростью Линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения (лоренцево или релятивистское сокращение длины). Длительность события в разных системах отсчета также связана аналогическими соотношениями: Формула геометрического сложения скоростей классической механики ( Инвариантность скорости света (второй постулат Эйнштейна) установлен как опытный факт. Схематически этот опыт можно представить таким образом (рис.32). По законам классической механики, скорость света с в разных инерциальных системах отсчета, представленных на рис. 32 а), б), в), г), должна быть различной: с′=с+υ, с′=с′−υ, с′′′=
Но высокоточные опыты Майкельсона (1881г) и Морли (1887г) показали, что с=с′=с′′=с′′′. Этот результат можно было объяснить, предполагая, что; либо неверен принцип относительности (инвариантности) Галилея − Ньютона (формулы преобразования Галилея), либо неверна вся система законов электродинамики и оптики (уравнения Максвелла). В релятивистской механике масса появляется в новой ипостаси: если в классической механике масса характеризовала инертные и гравитационные свойства тел, то в законе взаимосвязи массы и энергии (А.Эйнштейн, 1905г. ) она проявляется еще и в качестве характеристики энергосодержания тела. Изменение массы тела (или системы) сопровождается пропорциональным изменением его энергии: Из (10) следует, что даже покоящееся тело ( Наименьшей энергией E0 тело (частица) обладает в системе отсчета, относительно которой оно покоится (
 атомного ядра меньше, чем сумма собственных масс частиц, входящих в ядро. Но несохранение массы покоя не означает нарушения закона сохранения массы вообще. В теории относительности справедлив закон сохранения релятивистской массы. Он вытекает из формулы закона взаимосвязи массы и энергии E=mc2. В изолированной системе тел сохраняется полная энергия. Следовательно, сохраняется и релятивистская масса. В теории относительности законы сохранения энергии и релятивистской массы взаимосвязаны и представляют собой единый закон сохранения массы и энергии. Однако из этого закона отнюдь не следует возможность преобразования массы в энергию и обратно. Масса и энергия представляют собой два качественно различных свойства материи, отнюдь не «эквивалентных» друг другу. Ни один из известных опытных фактов не дает оснований для вывода о «переходе массы в энергию». Превращение энергии системы из одной формы в другую сопровождается превращением массы. Например, в явлении рождения и уничтожения пары электрон – позитрон, в полном соответствии с законом сохранения релятивистской массы и энергии, масса не переходит в энергию. Масса покоя частиц (электрона и позитрона) преобразуется в массу фотонов, т.е. в массу электромагнитного поля. атомного ядра меньше, чем сумма собственных масс частиц, входящих в ядро. Но несохранение массы покоя не означает нарушения закона сохранения массы вообще. В теории относительности справедлив закон сохранения релятивистской массы. Он вытекает из формулы закона взаимосвязи массы и энергии E=mc2. В изолированной системе тел сохраняется полная энергия. Следовательно, сохраняется и релятивистская масса. В теории относительности законы сохранения энергии и релятивистской массы взаимосвязаны и представляют собой единый закон сохранения массы и энергии. Однако из этого закона отнюдь не следует возможность преобразования массы в энергию и обратно. Масса и энергия представляют собой два качественно различных свойства материи, отнюдь не «эквивалентных» друг другу. Ни один из известных опытных фактов не дает оснований для вывода о «переходе массы в энергию». Превращение энергии системы из одной формы в другую сопровождается превращением массы. Например, в явлении рождения и уничтожения пары электрон – позитрон, в полном соответствии с законом сохранения релятивистской массы и энергии, масса не переходит в энергию. Масса покоя частиц (электрона и позитрона) преобразуется в массу фотонов, т.е. в массу электромагнитного поля.
Поскольку масса есть еще и мера количества материи, а энергия – мера движения материи, то этот фундаментальный закон природы – закон пропорциональности массы и энергии служит ярким подтверждением неразрывности материи и движения. Справедливость формулы (10) подтверждается в экспериментах с ядерными реакциями и в превращениях элементарных частиц. Таким образом, законы СТО более универсальны, чем законы классической механики: они применимы к любым скоростям движения, но для макротел, движущихся с малыми скоростями (по сравнению со скоростью светав вакууме) вполне достаточны более простые и удобные формулы классической механики. Законы классической механики получаются от формул релятивистской теории при Приложения 1 Потенциальные кривые Во многих задачах потенциальная энергия
tgα=mg зависит от m. Полная энергия E=Wk+Wp Если h=hmax, то Wk=0, Wp=E=mgh. Скорость тела на высоте h определяется из Wk=E−Wp →
где k − коэффициент упругости. С увеличением потенциальной энергии Wp, кинетическая энергия Wk уменьшается. Так как кинетическая энергия Wk не может быть отрицательным, то при полной энергии тела E, тело не может сместиться правее xmax и левее −xmax. Значит Wp не может быть больше чем E. Тело находиться как бы в потенциальной яме. В общем случае потенциальная кривая может иметь довольно сложный вид (рисунок а) внизу). Если Е − заданная полная энергия частицы, то частица может находиться только там, где Wp(x)≤E, т.е. в области I и III. Область II собой представляет потенциальный барьер, который частица не может преодолеть. В точках B и A ( Потенциальная кривая для взаимодействующих атомов или молекул изображена на рисунок б) внизу. При r → ∞, Wp(r) → 0. Если энергия частиц (W1p) невелика, то они не могут выходить из потенциальной ямы. При значении W2p связь между ними нарушается, и они расходятся на бесконечность.
Приложение 2 Сложение гармонических колебаний (одного направления и одинаковых частот)
x1=A1cos(ω0t+φ1) x2=A2cos(ω0t+φ2)
x=x1+x2=Acos(ω0t+φ), где A2=A12+A22+2A1A2cos(φ2−φ1)
использована формула −cos(180−(φ2−φ1))=cos(φ2−φ1) A=f(φ2−φ1) 1) когда φ2−φ1=±2mπ, (m=0,1,2,…), A=A1+A2 2) когда φ2−φ1=±(2m+1)π, (m=0,1,2..), A=|A1−A2| Биение получается когда ω2=ω1+Δω и Δω<<ω1 тогда x1=Acosωt x2=Acos(ω+Δω)t для простаты принято φ1 =φ2=0. в итоге x=x1+x2=(2Acos Aбиений=|2Acos
Любые сложные периодические колебания S=f(t) можно представить в виде суперпозиции гармонических колебаний с различными A, φ0, и частотами, кратными ω0 (Ряды Фурье, 1768−1830). Приложение 3 Затухающие колебания Затухающие колебания − это колебания, амплитуды которых из-за потерь энергии в реальном процесс с течением времени уменьшается. Линейные колебательные системы − идеализированные реальные системы, в которых параметры, определяющие физические свойств системы, в течение времени не меняются (например, пружинный маятник (когда справедлив закон Гука F=−kx), колебательный контур (L,C.R=const), математический маятник (ℓ,m=const)). Дифференциальное уравнение свободных затухающих колебаний линейной системы где s(t) − колеблющаяся величина, δ=const − коэффициент затухания, ω0 − циклическая частота свободных, незатухающих колебании при δ=0, (собственная частота колебательной системы). Решение уравнения ищем в виде s=e−δtu, где u=u(t) Уравнение похож на Определяя
Если и решение будет Тогда при s(t)=A0e−δt cos(ωt+φ), где A=A0e−δt − амплитуда затухающих колебаний, A0− начальная амплитуда.
Строго говоря, затухающие колебания не являются периодическими, однако если затухание мало, то можно пользоваться периодом между двумя последующими максимумами Декремент затухания A(t)/A(t+T)=eδT Логарифмический декремент затухания θ=ln{A(t)/A(t+T)}=δT=T/τ=1/Ne, где Ne − число колебания, совершаемых за время уменьшения амплитуды в e раз. Для данной системы θ=const Добротность Q=π/θ=πNe=π/δT0=ω0/2δ (при малых значениях Q, т.к. при δ2<<ω02, T≈T0). Приложение 4 Волновое уравнение − описывает распространение волн в однородной изотропной среде
или Это уравнение справедливо для любой волны, в частности и для плоской и для сферической волны. Например, для плоской волны имеем
Принцип суперпозиции (наложения) волн в линейной среде (т.е. в среде, свойства которой не изменяется под воздействием волны): каждая из волн распространяется так, как будто другие волны не существуют, а результатирующее смещение определяется геометрической суммой. Любая волна можно представить в виде волнового пакета (разложение Фурье) т.е. суперпозицией гармонических волн, мало отличающихся друг от друга по частоте. Например, две волны ξ1 и ξ2, (для простаты, приняты, что амплитуды равны A1=A2=A0, ω1=ω, ω2=ω+dω и dω<<ω, dk<<k): ξ1=A0 cos(ωt−kx) ξ2=A0 cos[(ω+dω)t−(k+dk)x], ξ=ξ1+ξ2= A(x,t)=2A0(tdω−xdk)/2 − новая амплитуда, которая отличается от гармонической тем, что она есть медленно изменяющая функция координаты х и времени t. Как скорость распространения этого волнового пакета принимают скорость перемещения максимума аплитуды A. При условии, что tdω−xdk=const, Это справедливо и для множеств суперпозирующих волн. Связь между
В недиспергирующей среде υ≠υ(λ) dυ/dλ=0 u=υ. При измерении дальности в радиолокации, в системах управления космическими объектами фигурирует именно u. В теории относительности доказывается, что групповая скорость u ≤ c, в то время как для фазовой скорости υ ограничений не существует.
(Детлаф А.А., Яворский Б.М. − Курс физики, М. «Высшая школа» 2000г.)
§ 29.2
Уравнение плоской волны по → + x, s=f(t−x/υ) Уравнение плоской синусоидальной волны по → +x s=Asin[ω(t−x/υ)+φ0] или Учитывая λ=υ∙T и волновое число s=Asin(ωt−kx+φ0) Уравнение сферической волны s=φ(r)f(t−r/υ) Уравнение синусоидальной сферической волны s=A(r)sin(ωt−kx+φ0) Волновое уравнение в линейной, однородной, изотропной, непоглощающей среде:
где Для синусоидальной волны υ − фазовая скорость, скорость распространения точек с фиксированной фазой, т.е. ωt−kx+φ=const → групповая скорость
§ 29.6
Стоящая волна при наложении двух когерентных бегущих плоских волн (навстречу друг другу) s1=Asin(ωt−kx); s2=Asin(ωt+kx+α); где α −разность фаз в точках x=0 s=s1+s2=2A∙cos(kx+α/2)∙sin(ωt+α/2) Астоящ = 2A∙cos(kx+α/2)∙ зависит от х, sin(ωt+α/2) не зависит от x. В стоящей волне все точки между двумя узлами колеблются с различными Астоящ, но с одинаковыми фазами (синфазн).
Приложение 5 Опыты Альберта Майкельсона (1881г) и
Майкельсона − Эдварда Морли (1887г.) Свет, проходя через плоскопараллельную стеклянную пластинку с полупрозрачным слоем серебра, раздваивается на взаимно перпендикулярные лучи, которые, отражаясь от двух зеркал (С1 и С2), в зрительной трубе создают интерференционные полосы. Вторая плоскопараллельная, но не посеребренная, пластина служит для компенсации разности хода лучей, возникающей из-за того, что один луч проходит сквозь толщу первой пластинки дважды, а торой луч − ни разу. Очевидно, что перемещение зеркала С2 вызовет смещение интерференционных полос. Если это перемещение составляет nλ/2 (где n =1.2.3….; λ −длина волны используемого света), то полосы сместятся на расстояние, равное n − кратному расстоянию между двумя соседними максимумами (минимумами) интерференционной картины. Это позволяет очень точно измерять длину световой волны. Именно таким методом была впервые измерена длина волны (в вакууме) излучения, соответствующего переходу между уровнями 2p10 и 5d5 атома криптона-86. Эта длина волны была принята за эталон (в данный момент устаревший) единицы длины − метра. Посредством интерферометра Майкельсона был осуществлен опыт Майкельсона, сыгравший исключительно важную роль в истории развития науки. Майкельсон поставил свой опыт в 1881г. с целью обнаружить движение Земли относительно мирового эфира и измерить скорость этого движения. Напомним, что по представлениям того времени мировой эфир являлся особой абсолютно неподвижной материальной средой − носительницей световых волн, скорость света в которой с=3∙108м/с. Очевидно, что интерференционные полосы, наблюдаемые в зрительной трубе интерферометра Майкельсона, покоящегося относительно мирового эфира, не будут смещаться при повороте интерферометра вокруг вертикальной оси, проходящей через середину О пластинки с полупрозрачным слоем серебра, поскольку его поворот не изменит разности хода лучей. Но интерферометр не покоится, а движется относительно мирового эфира вместе с Землей по ее орбите со скоростью υ. В этих условиях скорость света с должна векторно складываться со скоростью υ Земли. Поэтому скорость (и время) распространения света вдоль лучей ОС2 и ОС1 будет теперь различной, зависящей от направления этих лучей. Следовательно, при повороте интерферометра разность хода этих лучей и должна изменяться. При этом в зрительной трубе наблюдается смещение интерференционных полос, по которому можно определить υ. Пусть интерферометр ориентирован так, что он движется относительно эфира в направлении ОС2, а плечи интерферометра равны соответственно |OC2|=ℓ1 и | OC1|=ℓ2. Вычислим время t1 прохождения светом пути OC2O. Очевидно, что скорость распространения света относительно интерферометра на участке OC2 равна (c−υ), а на участке |OC2| −(c+υ), так как в первом случае направления υ и c совпадают, а во втором − взаимно противоположны. Тогда
а путь, пройденный светом относительно эфира,
Из рисунка следует, что Но свет проходит путь ℓ со скоростью c за то же время, за которое интерферометр проходит путь OO ′ со скоростью υ. Поэтому |OO′|/ℓ=υ/c, откуда | OO′ |= υℓ/c. Подставляя это выражение ℓ, получим, что
Обусловленная движением интерферометра разность хода лучей ОС2 и ОС1
Если повернуть интерферометр на 900, то его плечи ℓ1 и ℓ2 поменяются местами и разность хода лучей станет уже другой, равной
Таким образом, при повороте интерферометра на 900 разность хода лучей должна измениться на значение
которое вполне можно измерить по сопровождающему поворот смещению интерференционных полос, после чего легко рассчитать значение скорости υ Земли. (υ/c)2 для движения Земли У Майкельсона ℓ1=ℓ2=11м, λ0=590нм и число полос, на которое сместится интерференционная картина (использовано приближение для малых х, Точность прибора в опытах Майкельсона позволял обнаружить смещение 0,01 полосы, а ∆c < 8км/с т.е. <0,0003% (В 1959г. − ∆c<23мм/с, а ∆c/c≈10−10, в 1979г. − ∆c<10−3мм/с, ∆c≈3∙10−15) Однако опыты Майкельсона, проведенные и днем, и ночью, в разные время года, неожиданно дали отрицательный результат: никакого смещения интерференционных полос при повороте интерферометра не происходило! Отрицательный результат опыта Майкельсона можно было бы объяснить зависимостью скорости света от скорости движения его источника. Но опыты по наблюдению за двойными звездами отвергли такую возможность. Отметим, что гипотезы об увлечении мирового эфира движущимся телом, которые могли бы объяснить отрицательный результат опыта Майкельсона, тоже не получили экспериментального подтверждения. Поэтому результат опыта Майкельсона допускает только одно истолкование: скорость распространения в вакууме электромагнитных волн, в том числе света, одинакова во всех инерциальных системах отсчета независимо от их относительных скоростей движения. Вместе с тем из этого опыта следует, что мирового эфира не существует.
М О Л Е К У Л Я Р Н А Я Ф И З И К А И Т Е Р М О Д И Н А М И К А
Молекулярная физика – раздел физики, изучающий строение и свойства вещества, исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из атомов и молекул, находящихся в непрерывном хаотическом движении. В молекулярной физике применяют статистический (молекулярно – кинематический) метод исследования, который основан на том, что свойства макроскопической системы в конечном счете являются усредненными значениями динамических характеристик молекул, из которых состоят эти макроскопические тела. Например, температура тела определяется скоростью хаотического движения его молекул и выражается через среднее значение скорости движения всех молекул (нельзя говорить о температуре одной молекулы). Термодинамика - раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия и процессы перехода между этими состояниями. Система находится в состоянии термодинамического равновесия, если ее термодинамические параметры (параметры состояния) не меняются с течением времени при неизменности внешних условий. Термодинамика изучает количественные закономерности превращения энергии в различных процессах (тепловых, механических, электрических, магнитных и др.), обусловленного тепловым (беспорядочным) движением молекул, но не рассматривая микропроцессы, и этим отличается от молекулярной физики. Термодинамика базируется на двух началах – фундаментальных законах, установленных в результате обобщения опытных данных. Изучая одну и ту же систему, молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, отличаясь лишь различными методами исследования.
§ 1. Параметры термодинамических систем (параметры состояния)
Термодинамической системой называется макроскопическое тело (или группа тел), которому свойственны процессы, сопровождающиеся переходом теплоты в другие виды энергии, и обратные процессы. Параметрами термодинамических систем называется совокупность физических величин, которые характеризуют те или иные свойства термодинамической системы. Обычно в качестве таких параметров состояния выбирают температуру (Т), давление (р) и объем (V). Температура – физическая величина, количественно описывающая интенсивность хаотического движения атомов и молекул (или вообще частиц) термодинамической системы. Сейчас широко применяются две температурные шкалы: · Термодинамическая абсолютная температура, илитемпература Кельвина (К) (в формулах обозначается T). · Международная практическая температура, или температура Цельсия (0 С) (в формулах обозначается t). Реперные, или опорные, точки для шкалы Цельсия − это температуры замерзания (00) и кипения (1000) воды (при нормальном давлении). Для шкалы Кельвина реперная точка − это тройная точка воды (температура, при которой лед, вода и насыщенный пар находятся в термодинамическом равновесии), температура которой равна 273,15 К. Так как 1 K=10C, то T=273,15+t Температура T=0 К называется нулем Кельвина или абсолютным нулем, который недостижим (в 1993г. в лабораториях была достигнута самая низкая температура Т = 280 пК=2,8.10-10 К). Давление р − физическая величина, определяемая нормальной силой на единицу площади. Единица давления – паскаль (П а): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1м2 (1 Па = 1 Н/м2). Так как в молекулярной физике мы имеем дело с огромным количеством молекул, размеры и массы которых очень малы[10], то целесообразно применение более удобных единиц измерения для масс и количества молекул. Масса молекул (атомов) измеряется относительной атомной (молекулярной) массой Ar (Мr) (или просто атомной (молекулярной) массой или весом) - безразмерной величиной, равная отношению средней массы атома (молекулы) природной смеси изотопов элемента к 1/12 массе атома углерода 12С. Атомная единица массы - 1а.е.м.= 1/12 массы 12С. Ar или (Мr)= Но масса атомов или молекул не являются мерой количества вещества (как, например, плотность вещества не являетс
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 856; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |

 , где
, где  − волновое число.
− волновое число.
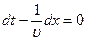 или dx/dt=υ.
или dx/dt=υ.
 (
( ) вдоль оси ОХ. Для простоты отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис.31. Связь между координатами произвольной точки в обеих системах имеет вид: x=x'+ut; y=y'; z=z' (преобразования координат Галилея).
) вдоль оси ОХ. Для простоты отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис.31. Связь между координатами произвольной точки в обеих системах имеет вид: x=x'+ut; y=y'; z=z' (преобразования координат Галилея). ;
;  , т. к.
, т. к.  Таким образом, уравнения динамики (
Таким образом, уравнения динамики ( ) при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям координат.
) при переходе от одной инерциальной системы отсчета к другой не изменяются, т.е. являются инвариантными по отношению к преобразованиям координат.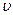 <<c превращаются в преобразования Галилея (табл. 3).
<<c превращаются в преобразования Галилея (табл. 3).

 где
где 
 , который появляется у релятивистских физических величин и при
, который появляется у релятивистских физических величин и при  , где m0 − масса этого тела в покое. Отсюда следует, что если
, где m0 − масса этого тела в покое. Отсюда следует, что если  , то тело не может двигаться со скоростью
, то тело не может двигаться со скоростью  получается от классического импульса
получается от классического импульса  при замене классической массы на релятивистскую.
при замене классической массы на релятивистскую.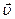 системе получается:
системе получается:  , где
, где  и
и 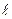 - длины в системе покоя и в движущейся системе соответственно.
- длины в системе покоя и в движущейся системе соответственно. , где Δt − промежутоквремени в системе покоя, а t0 – промежуток времени в движущейся системе (релятивистское замедление времени). Часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.
, где Δt − промежутоквремени в системе покоя, а t0 – промежуток времени в движущейся системе (релятивистское замедление времени). Часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов.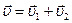 ) в СТО принимает вид:
) в СТО принимает вид:  . (9)
. (9) .
.
 . Или, полная энергия системы равна произведению ее массы на квадрат скорости в вакууме:
. Или, полная энергия системы равна произведению ее массы на квадрат скорости в вакууме:  (10)
(10) ) обладает с обственной энергией, или энергией покоя E0=m0c2.
) обладает с обственной энергией, или энергией покоя E0=m0c2. , кинетической энергии всех частиц и потенциальной энергии их взаимодействия. Поэтому
, кинетической энергии всех частиц и потенциальной энергии их взаимодействия. Поэтому  и
и  , где
, где  – масса покоя i- й частицы.
– масса покоя i- й частицы. функция от одной переменной (например, от координаты х,
функция от одной переменной (например, от координаты х,  = mgh,
= mgh,  ). График потенциальной энергии
). График потенциальной энергии  от этой переменной называется потенциальной кривой.
от этой переменной называется потенциальной кривой. На рисунке внизу − потенциальная кривая гравитационного поля в зависимости от высоты (h).
На рисунке внизу − потенциальная кривая гравитационного поля в зависимости от высоты (h).
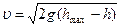
 Зависимость потенциальной кривой упругой деформации от деформации х имеет вид параболы (рис. направо),
Зависимость потенциальной кривой упругой деформации от деформации х имеет вид параболы (рис. направо),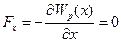 ) частица находится в равновесии (в точке B имеем устойчивое равновесие, а в точке A − неустойчивое).
) частица находится в равновесии (в точке B имеем устойчивое равновесие, а в точке A − неустойчивое).

 т.к. ω0=const, то φ2−φ1=const
т.к. ω0=const, то φ2−φ1=const
 t)cosωt, т.к.
t)cosωt, т.к. 

 ,
, с решением s=A0cos(ω0t+φ)
с решением s=A0cos(ω0t+φ) и
и  , и поставляя в основное уравнение, получим
, и поставляя в основное уравнение, получим

 , то можно брать
, то можно брать 

 ,
, − время, в течение которого амплитуда колебания уменьшается е раз (время релаксации).
− время, в течение которого амплитуда колебания уменьшается е раз (время релаксации). .
.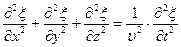
 , где ξ=ξ(x,y,z,t) − (кси) функция от координат и времени,
, где ξ=ξ(x,y,z,t) − (кси) функция от координат и времени,  − оператор Лапласа.
− оператор Лапласа.

 − групповая скорость.
− групповая скорость. и
и  , учитывая, что k=2π/λ
, учитывая, что k=2π/λ
 u может быть больше или меньше υ, в зависимости от знака dυ/dλ/.
u может быть больше или меньше υ, в зависимости от знака dυ/dλ/.
 ,
,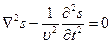
 Оператор Лапласа
Оператор Лапласа
 ,
, т.к. ω=υk, k=2π/λ, dk=−2πdλ/λ2
т.к. ω=υk, k=2π/λ, dk=−2πdλ/λ2

 ,
,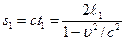 .
. Для определения пути s2=|OC1′O′′|=2ℓ, проходимого светом вдоль луча OC1 относительно эфира, найдем положения точки O и зеркала C1 для трех моментов времени (рисунок налево): когда свет проходит O (положения O и C1), когда он отражается от зеркала C1 (положения O′ и C′1) и когда он возвращается в O (положения O′′ и C1′′).
Для определения пути s2=|OC1′O′′|=2ℓ, проходимого светом вдоль луча OC1 относительно эфира, найдем положения точки O и зеркала C1 для трех моментов времени (рисунок налево): когда свет проходит O (положения O и C1), когда он отражается от зеркала C1 (положения O′ и C′1) и когда он возвращается в O (положения O′′ и C1′′).
 и
и 
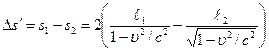

 ,
,

 и
и  .
. , где m0 и m0(
, где m0 и m0(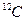 ) − масса атома или молекулы и масса атома углерода
) − масса атома или молекулы и масса атома углерода 


