
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция волн с одинаковыми частотамиСодержание книги
Поиск на нашем сайте
При наложении двух плоских волн с одинаковыми частотами, волновыми векторами и амплитудами, распространяющихся вдоль одной прямой, выражения (10) и (11) сводятся к следующим:
В этом случае амплитуда суммарной волны зависит только от разницы фаз k D x = k (x 01- x 02), которые волны набирают при распространении от своих источников до точки наблюдения. Так, если D x равно целому числу волн
колебания двух волн во всех точках пространства происходят в фазе, что приводит к их взаимному усилению. Если же D x равно не четному числу полуволн
амплитуда суммарной волны рана нулю - колебания двух волн в точке наблюдения происходят в противофазе, что приводит к их взаимному гашению. Стоячие волны При интерференции волн с одинаковыми частотами особо интересен случай, когда две волны с одинаковыми амплитудами распространяются навстречу друг другу:
При этом, если поместить начало системы координат между источниками на равном от них удалении (x 01=- x 02), то уравнение суммарной волны имеет максимально простой вид:
Возбуждение среды, описываемое уравнением типа (18), называется стоячей волной. Происхождение этого термина понятно – уравнение (18) не описывает характерного для волн перемещения фазы колебания в пространстве. Амплитуда колебаний в стоячей волне зависит от координаты:
Точки лежащие вдоль x на расстоянии l/2 колеблются в противофазе (см. рисунок 2). Точки, в которых А = 0, называются узлами, точки, в которых А = ± 2 a, называются пучностями стоячей волны. Длиной стоячей волны lст называется расстояние между ближайшими узлами. Очевидно, что lст= l/2. В связи с введением понятия стоячей волны уместно выделять волны бегущие, т.е. волны, в которых происходит перемещение фазы колебаний в пространстве. Бегущие волны описываются выражением (1). КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ К РАЗДЕЛУ 1. *Познакомьтесь с описанием синусоидальных волн с помощью комплексных чисел. Освойте метод векторных диаграмм сложения колебаний. Получите с помощью этого метода выражение для суммы двух колебаний с разными частотами и разными фазами. 2. Объясните с точки зрения теории упругости, почему в газах и жидкостях отсутствуют поперечные волны.
3. *Пусть имеется полубесконечная абсолютно упругая среда. К плоской границе среды равномерно по площади приложена нормальная сила меняющаяся со временем по закону синуса достаточно долго. Запишите уравнение движения для единичного объема этой среды. Покажите, что для неоднородных квазистатических деформаций это уравнение имеет вид волнового уравнения (4), где фазовая скорость волны (в данном случае, очевидно, продольной) связана с модулем Юнга и плотностью среды выражением
4. *Повторите рассуждения предыдущего задания для случая тангенциальной силы и получите для фазовой скорости поперечной волны соотношение
где G - модуль сдвига. 5. На основании формул из двух предыдущих заданий и теории упругости сделайте вывод об относительных величинах фазовых скоростей продольной 6. Докажите, что в упругой среде, охваченной волновым процессом, существует избыток механической энергии, распределенной в пространстве с объемной плотностью
где a - амплитуда волны, w - ее частота, r - плотность среды. 7. В чем суть явления интерференции? Разберите случаи биений и интерференции волн с одинаковыми частотами1. 8. Объясните, почему в выражении (10) роль амплитуды играет функция косинуса а не синуса. 9. Существуют ли условия при которых две волны во всех точках пространства усиливают (ослабляют) друг друга? 10.Приведите примеры возникновения стоячих волн в ситуациях из повседневной жизни. 11.*Рассмотрите наложение двух волн с одинаковыми частотами и амплитудами, волновые векторы которых направлены под углом a и -a к оси X системы координат. Покажите, что в этом случае суммарное возбуждение среды может быть представлено как сумма стоячей и бегущей волн. ЛАБОРАТОРНАЯ РАБОТА N 61.
|
||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.202.169 (0.009 с.) |

 , (14)
, (14) . (15)
. (15) , (16)
, (16) , (17)
, (17)
 . (18)
. (18) (19)
(19) .
. ,
, и поперечных
и поперечных 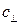 волн.
волн.



