
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
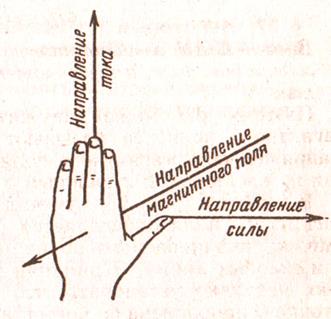
Рукоятка буравчика, ввинчиваемого по направлению тока, вращается в направлении магнитных силовых линий.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В отличие от силовых линий электрического поля магнитные силовые линии всегда замкнуты (вихревые или соленоидальные). Если силовые линии электрических полей начинаются от положительных зарядов и заканчиваются на отрицательных зарядах, то силовые линии магнитных полей не имеют ни начало, ни конца – еще одно доказательство отсутствия «магнит
ных зарядов». Еще 1820г. Ампер предполагал, что магнитные свойства обусловлено элементарными круговыми токами в этих постоянных магнитах.
Векторное произведение образует (по определению) правую систему Максимальное значение момента сил - Mmax, получается, когда Магнитная индукция Вектор магнитной индукции можно определить, используя аналоговый подход. Дело в том, что хотя, по сути, гравитационные, электрические и магнитные взаимодействия существенно отличаются друг от друга, закономерности их проявления, обнаруженные разными исследователями в разные времена, имеют много аналогов между собой. Поэтому мы, используя аналоговый подход, их характеристики будем рассматривать с единой точки зрения, не забывая, однако, что аналогия между ними не означает их идентичность. Многочисленные эксперименты показывают, что модули сил всех этих взаимодействий можно представить в виде
где A 1 , A 2 –характеристики носителей этих взаимодействий, а r - расстояние между ними. Существенно, что все эти силы с расстоянием уменьшаются одинаково – они обратно пропорциональны квадрату расстояния. Есть мнение, что это связанно с трехмерным объемом пространства: силы убивают с расстоянием по формуле 1/ r n-1 , где n - порядок пространства (мы живем в мире с n =3).
Для гравитационных взаимодействий носителями этих взаимодействий являются массы взаимодействующих тел m 1и m 2 (гравитационные массы). Для электрических взаимодействий носителями этих взаимодействий являются электрические заряды q 1и q 2. Для магнитных взаимодействий роль таких носителей играют элементы тока Переход от пропорциональности к равенству осуществляется коэффициентами, которые зависят от вида взаимодействия, от выбора систем единиц и определяется экспериментально. Для гравитационных взаимодействий этот коэффициент G = 6,67.10-11 Н.м2/кг2 (экспериментально определил Кавендиш 1798г.) называется гравитационной постоянной и не зависит от физических свойств среды. Для электрических взаимодействий в рационализированной системе единиц СИ этот коэффициент представляется в виде Для магнитных взаимодействий в рационализированной системе единиц СИ коэффициент пропорциональности имеет вид Элементарная сила магнитного взаимодействия между элементами тока (сила Ампера) определяется формулой: dF ~
Размерность и единица измерения м агнитной постоянной или магнитной проницаемости вакуума: μ0=1,26.10-6
По аналогу определения характеристики электрического поля - напряженности: dF=B·I2·dℓ·sinα, где
Единица магнитной индукции 1 Тесла (Тл) = 1 Тесла это магнитная индукция такого однородного магнитного поля, которое действует с силой 1Н на прямолинейный проводник длиной 1м и с током 1А, расположенный перпендикулярно силовым линиям магнитного поля. Существует также и напряженность магнитного поля, которая определяется как: dH = Размерность напряженности магнитного поля
Закон Ампера с напряженностью магнитного поля: dF=μ0 μ·H·I·dℓ·sinα. Магнитная индукция Так как Поток вектора магнитной индукции (магнитный поток) Ф через произвольную площадку dS, определяется как элементарный магнитный поток: где Bn - проекция вектора
Для однородного поля Магнитный поток Ф характеризуется числом линии индукции, пронизывающих площадку Единица измерения магнитного потока [Ф]=1 Вебер (Вб)=1 Тл·м2 При α=90о, модуль напряженности магнитного поля Напряженность магнитного поля направлена по касательной к силовой линии поля, а по модулю равна отношению силы, с которой поле действует на единичный элемент тока (расположенный перпендикулярно полю в вакууме) к магнитной постоянной. Примеры Индукция магнитного поля (ИМП) (по Трофимовой). 1. Конечного прямолинейного проводника с током. 2. Бесконечного прямолинейного проводника с током. 3. В центре кругового тока 4. На оси кругового тока. 5. Соленоида и тороида. Приложение закона Био-Савара-Лапласа для индукция магнитного поля
1. Индукция магнитного поля (ИМП) конечного прямолинейного проводника с током I.
Из-за очень маленьких значения dℓ и dα: AB=r·dα=dℓ·sinα,
Направление В перпендикулярно плоскости листа и обращено к нам.
2. ИМП бесконечного прямолинейного проводника с током. В этом случае можно использовать предыдущую формулу со значениями: α1=0, α2=180o, тогда Сравнить с характеристиками электрического поля;
3. ИМП в центре кругового тока.
В этом случае α=900, I=const, r=R=const
Так как ℓ=2πR
4. Разделив элементарную индукцию магнитного поля
Видно, что
Так как ℓ=2πR и При r0=0 совпадает с
5. Магнитное поле соленоида и тороида. Соленоидом называют катушку цилиндрической формы из проволки, витки которой намотаны в одном направлении. Магнитное поле вне соленоида внешне похож на поле магнита, а внутри длинного соленоида (когда длина соленоида ℓ больше чем его диаметр D; ℓ>>4−5D), однородно и где I − сила тока, ℓ −длина соленоида, n − число витков. Тороид − катушка из проволока, навитой на тор.
Магнитное поле вне тороида отсутствует, а внутри, однородно и
где I − сила тока, r −радиус тороидального кольца, n − число витков. §3.2. Вещество в магнитном поле Все вещества в магнитном поле намагничиваются. При этом: · Диамагнетики (вода, фосфор, сера, углерод, многие металлы – такие как золото, серебро, ртуть) ослабляют внешнее магнитное поле. · Парамагнетики (кислород, азот, некоторые металлы – алюминий, вольфрам, платина и др.) усиливают внешнее магнитное поле. Среди них: · Ферромагнетики (железо, никель, кобальт, некоторые сплавы и окиси этих металлов, а также сплавы марганца и хлора) дают очень большое усиление внешнего магнитного поля.
Магнитный момент атома (молекулы) вещества образуется геометрической суммой орбитальных и спиновых магнитных моментов электронов и собственного магнитного момента ядра.
У диамагнетиков эта геометрическая сумма всех магнитных моментов равняется нулю, поэтому их собственный магнитный момент атома тоже равняется нулю. Под воздействием внешнего магнитного поля у диамагнетиков появляется собственный магнитный момент, который направлен против внешнего магнитного поля и ослабевает его. Когда внешнее поле исчезает, диамагнетик размагничивается. У парамагнетиков геометрическая сумма всех магнитных моментов не равняется нулю, но при отсутствии внешнего поля они ориентированы беспорядочно (хаотично), поэтому общее поле парамагнетиков равняется нулю. В присутствии внешнего магнитного поля происходит переориентация собственных магнитных моментов атомов парамагнетиков вдоль силовых линий внешнего магнитного поля, тем самым усиливая его. При исчезновении внешнего магнитного поля парамагнетики тоже размагничиваются.
Здесь тоже существует диамагнитный эффект, но он не заметен на фоне боле сильного парамагнетизма. Относительная магнитная проницаемость среды μ для вакуума μ=1 У диамагнетиков μ<1 У парамагнетиков μ>1 У ферромагнетиков μ~100−20000 Большие значения μ у ферромагнетиков обусловлено их особой структурой. Они имеют сравнительно крупные (~10-2мм) самопроизвольно намагниченных до насыщения областей (домены), в которых магнитные моменты всех атомов ориентированы одинаково. Количество атомов в доменах ~109. Под воздействием внешнего магнитного поля по их силовым линиям ориентируются не отдельные атомы, а домены, которые после исчезновения внешнего поля в какой то степени сохраняют приобретенную ориентацию, т.е. остаются намагниченными.
При выше некоторой температуры (температура Кюри) ферромагнетики теряют свои ферромагнитные свойства и превращаются в обычные парамагнетики с μ≈1 (например, для железа эта температура ~ 10000). У ферромагнетиков μ зависит от напряженности внешнего магнитного поля H, хотя формула B=μ0μH справедлива для них, но B~H, а μ=μ(H). Из соотношения B=μ0μH, учитывая, что для вакуума μ = 1, то для вакуума (обозначая индукцию магнитного поля в вакууме B0) получаем B0=μ0 H, и B=μB0.. Отсюда и определение Относительная магнитная проницаемость среды μ показывает, во сколько раз изменяется индукция магнитного поля, существовавшего в пустоте, если пространство, охваченное этим полем, заполняется данной средой. Напряженность магнитного поля Если сравнивать с характеристиками электростатического поля
Но исторически так сложилось, что им даны противоположные названия.
§3.3. Рамка с током в магнитном поле (Применения закона Ампера)
Изучая действия магнитного поля на электрический ток Ампер (1820) эмпирически нашел, что в однородном магнитном поле с постоянной индукцией В на прямолинейный элемент тока IΔℓ действует сила: FA=I·B·Δℓ·sinα. Где α − угол между направлением тока в проводнике и вектором индукции, а Направление силы определяется правилом левой руки. FA всегда перпендикулярна плоскости, где находятся Для сложной формы проводники и для неоднородного поля:
Силы ампера не являются центральными, у них нет силового центра как у гравитационных или кулоновских сил. На рамку с током в магнитном поле со стороны магнитного поля действует пара сил, которая (при определенном ориентации рамки), поворачивает рамку вокруг своей оси. Поворот осуществляется таким образом, что вектор магнитного момента рамки
Ориентирующее действие магнитного поля на рамку с током лежит в основе устройства многих электроизмерительных приборов (гальванометры, вольтметры, амперметры). §3.4. Сила Лоренца
Сила Ампера означает, что аналогичная сила действует и на каждый движущий заряд. Сила, действующая на электрический заряд q, движущий в магнитном поле со скоростью υ, называется силой Лоренца. Ее можно определить, если силу Ампера, которая действует на все движущие заряда, делить на количество этих зарядов N: Приняв N=n·V, где n− плотность зарядов в объеме V, а V=SΔℓ, где S− сечение проводника, Δℓ− путь, который проходит заряд, двигаясьсо скоростью
fЛ=q·υ·B·sin( В простейшем случае, если принять электрический ток как движение одного заряда, также получим: FA=I·B·Δℓ·sinα, I=q/t, Δℓ/t=υ, то fЛ=q·υ·B·sinα, где α−угол между векторами
Направление fЛ определяется с помощью правила левой руки: если ладонь левой руки расположить так, что в нее входил вектор  , а четыре вытянутых пальца направить вдоль вектора , а четыре вытянутых пальца направить вдоль вектора 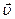 (для q>0 направление I и (для q>0 направление I и 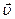 совпадают, для q<0 − противоположны ), то отогнутый большой палец покажет направление fЛ. (Напоминаем, что направлением тока принимается направление движения положительных зарядов). совпадают, для q<0 − противоположны ), то отогнутый большой палец покажет направление fЛ. (Напоминаем, что направлением тока принимается направление движения положительных зарядов).
Сила Лоренца действует только на движущийся относительно магнитного поля заряд (в рассматриваемой системе координат, когда Так как fЛ всегда перпендикулярно вектору скорости, сила Лоренца не совершает работу и не изменяет кинетической энергии свободной частицы. При движении заряженной частицы в магнитном поле может изменяться только направление скорости, но не ее модуль.
§3.5. Движение заряженных частиц в электрическом поле При движении вдоль линии напряженности электрического поля, действующая на заряд сила Если начальная скорость υ≈0, то приобретенная или потерянная кинетическая энергия mυ2/2=eU. В случае, когда
(парабола)
Заметим, что Изменяя Е получаем разные точки А на экране и этим можем определить удельный заряд. §3.6. Движение заряженных частиц в магнитном поле
Период вращения (не зависит от Если частица влетает в магнитное поле под углом α к линиям индукции, то ее траектория – винтовая линия, ось которой совпадает с направлением
Обратное воздействие –«превратил магнетизм в электричество» М.Фарадей (1831г.) (переплетчик книг?) Электрический ток, возбуждаемый магнитным полем в замкнутом контуре, называется индуцированным, а само явление возбуждения тока посредством магнитного поля – электромагнитной индукцией. Электродвижущая сила, обусловливающая индукционный ток, называется электродвижущей силой индукции.
В замкнутом контуре индуцируется ток во всех случаях, когда происходит изменение потока магнитной индукции сквозь площадь, ограниченную контуром. Электродвижущая сила индукции εi пропорциональна скорости изменения потока магнитной индукции ( Закон Фарадея ): εi~ где Ф – поток магнитной индукции. Закон Фарадея всегда дополняется правилом Ленца (1833г.): Индуцированный ток имеет такое направление, что его собственное магнитное поле компенсирует изменение потока магнитной индукции, вызывающее этот ток. Учитывая правило Ленца, и то, что из закона Фарадея определяется единица измерения магнитного потока (поэтому коэффициент пропорциональности можно принять k=1), для окончательного вида закона Фарадея-Ленца имеем: εi ═ – Знак минус, математически выражая правило Ленца, показывает, что если поток увеличивается (dФ>0), то εi<0 и поле индуцированного тока направлено навстречу потоку; если же поток уменьшается (dФ<0), то εi>0 и направление родительского поля и поля индуцированного тока совпадают. Правило Ленца позволяет нам определить направление индуцированного тока. Для этого надо: а) определить направление магнитного потока через контур (направление силовых линий В магнитного поля), б) определить как меняется магнитный поток (увеличивается или уменьшается dФ/dt), в) используя правило Ленца, определить направление силовых линий Bi индуцированного магнитного поля, г) зная направление силовых линий индуцированного магнитного поля, определить направление индуцированного тока Ii, создавшего это поле (обычно по правилу правой руки). Как уже отмечалось, из закона Фарадея-Ленца можно по другому определить единицу измерения магнитного потока вебер (Вб). 1 вебер это такой поток магнитной индукции сквозь площадь, ограниченную контуром, при убывании которого до нуля, за 1 с, в контуре индуцируется электродвижущая сила, равная 1 В.
Следует отметить, что: · а) Индуцированный ток (индуцированная ЭДС) в контуре появляется всегда, независимо от способа изменения магнитного потока; это может быть и магнитный поток переменного тока, и изменение площади контура, и т. п.. · б) Для индуцирования ЭДС переменным потоком магнитного поля присутствие замкнутого проводящего контура необязательно. Индуцированная ЭДС всегда образуется в областях пространства, где происходить изменение потока магнитного поля: проводящий контур играет лишь роль индикатора. Если говорить о природе εi, то в случаях движения контура в магнитном поле ЭДС индукции обусловлена действием лоренцевой силы на заряды, находящиеся в контуре и движущиеся вместе с ним. (Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.) В случае же неподвижного контура, находящегося в переменном (нестационарном) магнитном поле, возникновение εi связанна с вихревыми электрическими полями, о существование которых впервые высказал Д. К. Максвелл (1864г.). Он объяснил это тем, что переменное магнитное поле создает в пространстве переменное электрическое поле и линии напряженности магнитного поля концентрически охвачены линиями напряженности электрического поля. Вихревые электрические поля, в отличие от электростатических полей, создаваемые неподвижными, постоянными электрическими зарядами, не потенциальны. Напомним, что электростатические поля, создаваемые неподвижными, постоянными электрическими зарядами, потенциальны (не вихревыми). Силовые линии этих полей незамкнуты – они начинаются от положительных зарядов и кончаются на отрицательных зарядах. В этих полях работа по замкнутым траекториям равняется нулю. Вихревые электрические поля имеют замкнутые силовые линии и силы этого поля разделяют заряды в проводящем контуре, создавая в нем εi: для них Индуцированные токи возникают и в массивных сплошных проводниках, пронизываемых изменяющимся магнитным полем (токи Фуко). Они могут быть и полезными (например, для плавки металлов), и нежелательными или вредными (по этому в трансформаторах и других электроприборах сердечники делают из изолированных пластин или из феррита, у которых электрическое сопротивление очень большое и, следовательно, вихревые токи малы).
§3.8. Закон Ома для полной цепи (из Лаврова И.В., Курс физики,1981,стр.90)
Сила Ампера FA=IBℓ
За это время источник расходует энергию εIdt на выделение джоулева тепла I2Rdt и перемещение перемычки. (R – сопротивление контуры). По закону сохранения энергии εIdt=I2Rdt+IBℓdx. Считая I=const и Bℓdx=dФ - изменение магнитного потока, получаем
Т.е.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.179.239 (0.016 с.) |

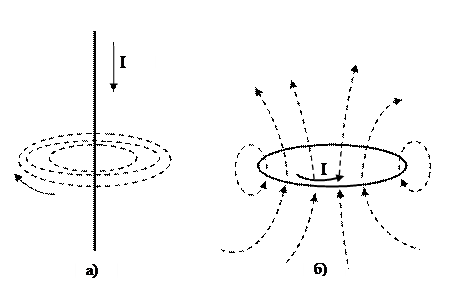
 Магнитные свойства контура с током I можно характеризовать вектором м агнитного момента
Магнитные свойства контура с током I можно характеризовать вектором м агнитного момента  , где S - площадь контура, а
, где S - площадь контура, а 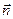 - нормаль к ней.
- нормаль к ней. На рамку в магнитном поле действует пара сил и вращающий момент сил
На рамку в магнитном поле действует пара сил и вращающий момент сил 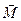 зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой:
зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой:  , где
, где  - вектор магнитной индукции (количественная характеристика магнитного поля).
- вектор магнитной индукции (количественная характеристика магнитного поля).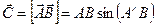
 ,поэтому в данной точке поля Mm/pm=B=const.
,поэтому в данной точке поля Mm/pm=B=const. направлена по
направлена по  .
. и
и 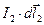 , которые собой представляют векторы, модули которых равны произведению бесконечно малого участка длины проводника на силу тока в нем.
, которые собой представляют векторы, модули которых равны произведению бесконечно малого участка длины проводника на силу тока в нем. , где
, где  = 8,85.10-12 Кл2/(Н.м2) электрическая постоянная, а
= 8,85.10-12 Кл2/(Н.м2) электрическая постоянная, а  - диэлектрическая проницаемость среды, характеризующая электрические свойства данной среды.
- диэлектрическая проницаемость среды, характеризующая электрические свойства данной среды. , где
, где  = 4π.10-7 Н/А2 - магнитная постоянная (зависит от выбора системы единиц), а
= 4π.10-7 Н/А2 - магнитная постоянная (зависит от выбора системы единиц), а  - относительная магнитная проницаемость (или просто магнитная проницаемость) среды, характеризующая магнитные свойства среды, ее способность намагничиваться под влиянием внешнего магнитного плоя. μ0μ − абсолютная магнитная проницаемость среды.
- относительная магнитная проницаемость (или просто магнитная проницаемость) среды, характеризующая магнитные свойства среды, ее способность намагничиваться под влиянием внешнего магнитного плоя. μ0μ − абсолютная магнитная проницаемость среды. , а более точно
, а более точно  и
и , где
, где  или
или 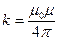 .
. =м·кг·с-2·А-2=Н/А-2= Гн/м (Генри на метр)
=м·кг·с-2·А-2=Н/А-2= Гн/м (Генри на метр)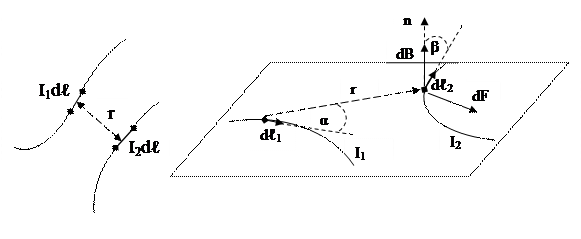
 ,
, 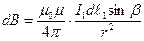 − магнитная индукция – характеристика магнитного поля, векторный вид которой
− магнитная индукция – характеристика магнитного поля, векторный вид которой  .
. Направление силы, действующая со стороны магнитного поля на провод с током, получаем из векторного уравнения
Направление силы, действующая со стороны магнитного поля на провод с током, получаем из векторного уравнения  (Закон Ампера), и определяется правилом правой руки. Если ладонь левой руки расположить так, чтобы вектор индукции магнитного поля входил в ладонь, а четыре вытянутых пальца направлялись вдоль тока, то отогнутый на 900 большой палец покажет направление силы, действующий на этот элемент тока.
(Закон Ампера), и определяется правилом правой руки. Если ладонь левой руки расположить так, чтобы вектор индукции магнитного поля входил в ладонь, а четыре вытянутых пальца направлялись вдоль тока, то отогнутый на 900 большой палец покажет направление силы, действующий на этот элемент тока.
 и
и  (Закон Био – Савара – Лапласа).
(Закон Био – Савара – Лапласа).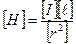 = А·м-1, а [ B ]=[ μ0 ]·[ H ].
= А·м-1, а [ B ]=[ μ0 ]·[ H ].
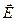 для электрического поля, поэтому для нее так же справедлив принцип суперпозиции: для
для электрического поля, поэтому для нее так же справедлив принцип суперпозиции: для  .
. , где
, где 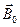 - магнитная индукция в вакууме.
- магнитная индукция в вакууме.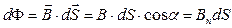 ,
, на направление нормали к площадке.
на направление нормали к площадке. Тогда
Тогда

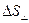 (и одновременно
(и одновременно  ).
). .
. Так как I=const,
Так как I=const,  ,
, BCA=α,
BCA=α, 


 , которая справедлива и при R<<ℓ.
, которая справедлива и при R<<ℓ. ,
,  .
.

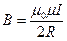
 ИМП на оси кругового тока.
ИМП на оси кругового тока. на взаимно перпендикулярные компоненты как на рисунке:
на взаимно перпендикулярные компоненты как на рисунке:  и
и 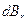 :
:

 друг друга компенсируют и
друг друга компенсируют и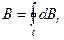

 ;
; 
 ,
, 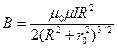 .
. или
или  ,
, или
или  ,
,




 .
. зависит только от макроскопических токов в проводнике и не зависит от среды. Индукция магнитного поля
зависит только от макроскопических токов в проводнике и не зависит от среды. Индукция магнитного поля  , то
, то 
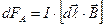
 становится параллельным вектору
становится параллельным вектору 

 )
)
 , ускоряет или замедляет движение заряда.
, ускоряет или замедляет движение заряда. : t=x/υ0. Сила Кулона
: t=x/υ0. Сила Кулона  .
. (Силой тяжести пренебрегаем)
(Силой тяжести пренебрегаем)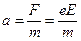


 - удельный заряд частицы.
- удельный заряд частицы. При движении заряженных частиц вдоль линии индукции
При движении заряженных частиц вдоль линии индукции  ), fЛ=0. При движении заряженных частиц поперек линии индукции магнитного поля (
), fЛ=0. При движении заряженных частиц поперек линии индукции магнитного поля ( ), fЛ ≠ 0, перпендикулярна
), fЛ ≠ 0, перпендикулярна 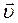 и сообщает частице центростремительное ускорение ац. Частица движется по окружности, радиус R которой определяется из соотношений:
и сообщает частице центростремительное ускорение ац. Частица движется по окружности, радиус R которой определяется из соотношений:  ,
, 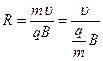 .
.

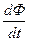
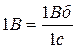 или 1 Вб =1 В.с =1 Тл.м2= 1
или 1 Вб =1 В.с =1 Тл.м2= 1 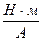
 Если за время dt перемычка перемещается на dx, то сила Ампера совершает работу IBℓdx.
Если за время dt перемычка перемещается на dx, то сила Ампера совершает работу IBℓdx. закон ОМА для полной цепи.
закон ОМА для полной цепи. -алгебраическая сумма ЭДС источника ε и ЭДС индукции εi.
-алгебраическая сумма ЭДС источника ε и ЭДС индукции εi. (закон Фарадея-Ленца).
(закон Фарадея-Ленца).


