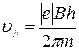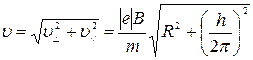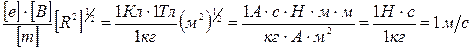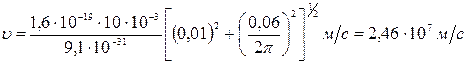Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
На контур с током в магнитном полеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Закон Био-Савара-Лапласа где
Магнитная индукция: в центре кругового тока поля бесконечно длинного прямого тока поля, созданного отрезком проводника с током поля бесконечно длинного соленоида где линией, соединяющей концы отрезка с точкой поля; R — радиус кругового тока; r — кратчайшее расстояние до оси проводника; n — число витков на единицу длины соленоида. Сила взаимодействия двух прямолинейных Бесконечно длинных параллельных токов На единицу их длины где r — расстояние между токами Работа по перемещению контура с током В магнитном поле где Ф — магнитный поток через поверхность контура. Магнитный поток однородного магнитного Поля через площадку S где нормалью к площадке. Закон электромагнитной индукции где N — число витков контура. Потокосцепление контура с током где L — индуктивность контура. Электродвижущая сила самоиндукции Индуктивность соленоида где V — объем соленоида;
Мгновенное значение силы тока в цепи, Обладающей сопротивлением R и индуктивностью L Энергия магнитного поля Объемная плотность энергии магнитного поля Примеры решения задач. Пример 18. Три точечных заряда Q1 = Q2 = Q3 = 1 нКл расположены в вершинах равностороннего треугольника. Какой заряд Q4 нужно помесить в центр треугольника, чтобы указанная система находилась в равновесии.
 = 0, (1) = 0, (1)
F- равнодействующая сил F2 и F3.
 F - F4 = 0, откуда F = F4. Выразим в последнем равенстве F через F2 и F3 и учитывая, что F2 = F3, получим: F - F4 = 0, откуда F = F4. Выразим в последнем равенстве F через F2 и F3 и учитывая, что F2 = F3, получим:
Применив закон Кулона и имея в виду, что Q1 = Q2 = Q3, найдем:
откуда
Из геометрических построений в равностороннем треугольнике следует, что
С учетом этого формула (2) примет вид:
Подставим числовые значения:
Пример 19. Два заряда Р е ш е н и е. 1.Напряженность электрического поля в точке A (рис. 7) является геометрической (т. е. векторной) суммой напряженностей
Модуль результирующий напряженности может быть найден по теореме косинусов как диагональ параллелограмма, построенного на векторах
где Q – заряд, создающий поле;
r – расстояние от расчётной точки поля до заряда, его создающего. Так как
Поскольку
Подставив выражение (3) и (4) в (1), получим:
Выразим числовые значения величин в СИ: Проверим формулу (5):
Подставим в формулу (5) числовые данные и вычислим
Примечание. В расчётную формулу (5) подставлены модули зарядов, поскольку их знаки учтены при выводе этой формулы. 2. Потенциал электрического поля в точке А равен алгебраической сумме потенциалов
Потенциал поля точечного заряда выражается формулой:
Подставив числовые значения величин в формулу (8), вычислим:
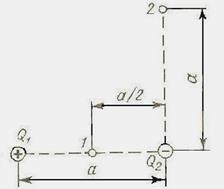
Пример 20. Электрическое поле создается двумя зарядами Q1 = 4мкКл и Q2 = -2 мкКл, находящимися на расстоянии а = 0,1 м друг от друга. Определить работу А1,2 сил поля по перемещению заряда Q = 50 нКл из точки 1 в точку 2 (рис. 8) Решение. Для определения работы А1,2 сил поля воспользуемся соотношением
Применяя принцип суперпозиции электрических полей, определим потенциалы φ1 и φ2 точек 1 и 2 поля:
Тогда
или
Проверим, даст ли правая часть равенства единицу работы,Дж:
Подставим числовые значения физических величин и произведем вычисления:
Пример 21. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью υ1 = 106 м/с, чтобы скорость его возросла в n = 2 раза. Решение. Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением элементарного заряда е на разность потенциалов U:
m- масса электрона; υ1 и υ2- начальная и конечная скорость его. Приравняв правые части равенства (1) и (2), получим:
где Отсюда искомая разность потенциалов равна:
Произведем вычисления:
Пример 22. Конденсатор емкостью С1 = 3 мкФ был заряжен до разности потенциалов U1 = 40 В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью С2 = 5 мкФ. Какая энергия W израсходуется на образование искры в момент присоединения второго конденсатора? Решение. Энергия, израсходованная на образование искры,
где W1- энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; W2- энергия, которую имеет батарея, составленная из двух конденсаторов. Энергия заряженного конденсатора определяется по формуле:
где С- емкость конденсатора или батареи конденсаторов. Выразив в формуле (1) энергии W1 и W2 по формуле (2) и приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим:
где U2- разность потенциалов на зажимах батареи конденсаторов. Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U2 следующим образом:
Подставив выражение U2 в формулу (3), найдем:
Пример 23. Потенциометр сопротивлением R = 100 Ом подключен к батарее с ЭДС ε = 150В и
где R1- сопротивление, параллельно соединенных вольтметра и половины потенциометра; I1- суммарная сила тока в ветвях этого соединения (она равна силе тока в неразветвленной части цепи). Силу тока I1 найдем по закону Ома для полной цепи:
где Re сопротивление внешней цепи. Это сопротивление есть сумма двух сопротивлений:
Сопротивление R1 найдем по формуле параллельного соединения проводников
Подставив в формулу (1) выражение Re по (2), найдем:
В данном случае решение задачи в общем виде было бы громоздким. Поэтому удобно вычисление величин провести раздельно:
2. Разность потенциалов между точками А и В при отключенном вольтметра равна произведению силы тока I2 на половину сопротивления потенциометра:
где I2 - сила тока в цепи при отключенном вольтметре. Ее определим по формуле:
Подставив выражение I2 в формулу (3), найдем:
Произведем вычисления:
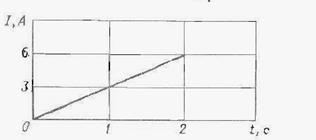
Пример 24. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Δt = 2 с по линейному закону от I0 = 0 до I = 6 А (рис 10). Определить теплоту Q1, выделившуюся в этом проводнике за первую секунду, и Q2,выделевшиюся за вторую, а также найти отношение Q2/ Q1.
Здесь сила тока I является некоторой функцией времени. В данном случае
где k-коэффициент пропорциональности, характеризующий скорости изменения силы тока:
С учетом выражения (2) формула (1) примет вид:
Для определения теплоты, выделившейся за конечный интервал времени Δt, выражение (3) надо проинтегрировать в пределах от t1 и t2:
Произведем вычисления:
Пример 25. Два параллельных бесконечно длинных провода D и С, по которым текут в одном направлении электрические токи силой I=60 А, расположены на расстоянии d=10 см друг от друга. Определить магнитную индукцию В поля, создаваемого проводниками с током в точке А (рис. 11), отстоящей от оси одного проводника на расстоянии r1 = 5 см, от другого —r2 = 12 см.
В=В1 + В2. Модуль вектора В может быть найден по теореме косинусов:
где α — угол между векторами В1 и В2. Магнитные индукции B1 и В2 выражаются соответственно через силу тока I и расстояния r1и г2 от проводов до точки А:
Подставляя выражения B1и B2в формулу (1) и вынося
Вычислим cos α. Заметив, что
где d — расстояние между проводами. Отсюда
Подставим в формулу (2) числовые значения физических величин и произведем вычисления:
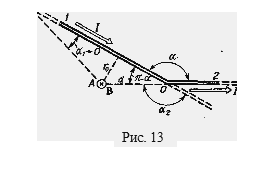
Пример 26. Длинный провод с током I= 50 А изогнут под углом Решение. Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О (рис. 13). В соответствии с принципом суперпозиции магнитных полей магнитная индукция В в точке А будет равна геометрической сумме магнитных индукции В1 и В2 полей, создаваемых отрезками длинных проводов 1 и 2, т. е. В=В1 + В2. Магнитная индукция В 2 равна нулю. Это следует из закона Био — Савара — Лапласа, согласно которому в точках, лежащих на оси привода,
Магнитную индукцию B1 найдем, воспользовавшись соотношением
где r0 — кратчайшее расстояние от провода 1до точки А (рис. 13).
Так как B = B1(B2=0), то
Вектор В сонаправлен с вектором В1 и определяется правилом правого винта. На рис. 13 это направление отмечено крестиком в кружочке (перпендикулярно плоскости чертежа, от нас). Произведем вычисления:
В = В1 + В2, где В1 — магнитная индукция поля, созданного в точке А током I1 ;В2 — магнитная индукция по-, созданного в точке Атоком I2. Заметим, что векторы B1 и В2 взаимно перпендикулярны (их направления находятся по правилу буравчика и изображены в двух проекциях на рис. 15). Тогда модуль вектора В можно определить по теореме Пифагора:
где B1и В2 определяются по формулам расчета магнитной индукции для бесконечно длинного прямолинейного провода с током:
В нашем случае r0 = d/2. Тогда
Произведем вычисления:
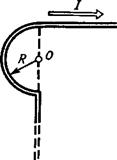
Пример 28. Бесконечно длинный провод изогнут так, как это изображено на рис. 16. Радиус R дуги окружности равен 10см. Определить магнитную индукцию В поля, создаваемого в точке О током I=80 А, текущим по этому проводу. Решение. Магнитную индукцию В в точке О найдем, используя принцип суперпозиции магнитных полей:
где B1, В2 и Вз — магнитные индукции в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках провода.
Так как точка О лежит на оси провода 1, то В1 = 0 и тогда
Учитывая, что векторы В2 и В3 направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, то геометрическое суммирование можно заменить алгебраическим:
Магнитную индукцию В2 найдем, воспользовавшись выражением для магнитной индукции в центре кругового тока:
В нашем случае магнитное поле в точке О создается лишь половиной кругового тока, поэтому
Магнитную индукцию В3 найдем, воспользовавшись соотношением
В нашем случае r0=R, α1=π/2 (cos α1=0),
Используя найденные выражения для В2 и В3, получим
или
Произведем вычисления:
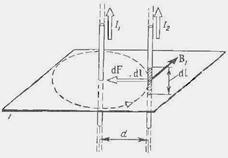
Пример 29. По двум параллельным прямым проводам длиной l=2,5м каждый, находящимся на расстоянии d=20 см друг от друга, текут одинаковые токи I=1 кА. Вычислить силу взаимодействия токов. Решение. Взаимодействие двух проводов, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой провод. Предположим, что оба тока (обозначим их для удобства I1 и I2) текут в одном направлении. Ток I1 создает в месте расположения второго провода (с током I2) магнитное поле. Проведем линию магнитной индукции (пунктир на рис. 18) через второй провод и по касательной к ней — вектор магнитной индукции В1. Модуль магнитной индукции В1 определяется соотношением
Согласно закону Ампера, на каждый элемент второго провода с током I2 длиной d l действует в магнитном поле сила
Подставив в это выражение B1согласно (1), получим
Силу F взаимодействия проводов с током найдем интегрированием:
Заметив, что I1 = I2 = I, получим
Убедимся в том, что правая часть этого равенства дает единицу силы (Н):
Произведем вычисления:
Сила F сонаправлена с силой dF (рис. 18) и определяется (в данном случае проще) правилом левой руки. Пример 30. Протон, прошедший ускоряющую разность потенциалов U = 600 В, влетел в однородное магнитное поле с индукцией B = 0,3 Тл и начал двигаться по окружности. Вычислить радиус R окружности.
где m — масса протона.
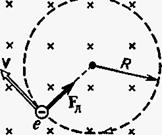
На рис. 19 совмещена траектория протона с плоскостью чертежа и дано (произвольно) направление вектора v. Силу Лоренца направим перпендикулярно вектору v к центру окружности (векторы аn и Fл сонаправлены). Используя правило левой руки, определим направление магнитных силовых линий (направление вектора В). Перепишем выражение (1) в скалярной форме (в проекции на радиус):
В скалярной форме Fл=Q vВ sinα. В нашем случае v
Отсюда находим радиус окружности: R=mv/(QB) (3) Заметив, что mv есть импульс протона (р), это выражение можно записать в виде R=p/(QB) Импульс протона найдем, воспользовавшись связью между работой сил электрического поля и изменением кинетической энергии протона, т.е. А = ΔТ, или Q(φ1- φ2)=T2-T1 где φ1-φ2 - ускоряющая разность потенциалов (или ускоряющее напряжение U); Т1 и Т2 — начальная и конечная кинетические энергии протона. Пренебрегая начальной кинетической энергией протона (Т1«0) и выразив кинетическую энергию Т2 через импульс р, получим QU=p2/(2m) Найдем из этого выражения импульс
или
Убедимся в том, что правая часть равенства дает единицу длины (м):
Подставим в формулу (4) числовые значения физических величин и произведем вычисления:
рис. 20 линии магнитной индукции перпендикулярны плоскости чертежа и направлены «от нас» (обозначены крестиками). Движение электрона по окружности эквивалентно круговому току, который в данном случае определяется выражением
где е — заряд электрона; Т — период его обращения. Период обращения можно выразить через скорость электрона v и путь, проходимый электроном за период Т = v/ (2лR). Тогда I экв=|е| v/(2πR) (1) Зная I экв, найдем магнитный момент эквивалентного кругового тока. По определению, магнитный момент контура с током выражается соотношением Рm=IэквS, (2) где S — площадь, ограниченная окружностью, описываемой электроном (S = πR2). Подставив Iэкв из (1) в выражение (2), получим
Сократим на πR и перепишем это выражение в виде:
В полученном выражении известной является скорость электрона, которая связана с радиусом R окружности, по которой он движется, соотношением R = mv/(QB) (см. пример 6). Заменив Q на │e│, найдем интересующую нас скорость v=\е\ВR/т и подставим ее в формулу (3):
Убедимся в том, что правая часть равенства дает единицу магнитного момента (А∙м2):
Произведем вычисления:
Пример 32. Электрон движется в однородном магнитном поле (В=10мТл) по винтовой линии, радиус R которой равен 1 см и шаг h = 6см. Определить период Т обращения электрона и его скорость v. Решение. Электрон будет двигаться по винтовой линии, если он влетает в однородное магнитное поле под некоторым углом (α≠π/2) к линиям магнитной индукции. Разложим, как это показано на рис. 21, скорость v электрона на две составляющие: параллельную вектору в(v) и перпендикулярную ему (v Период обращения электрона связан с перпендикулярной составляющей скорости соотношением Т=2πR/ v Найдем отношение R/ v
или
где v
R/v и подставим его в формулу (1):
Убедимся в том, что правая часть равенства дает единицу времени (с):
Произведем вычисления:
Модуль скорости v, как это видно из рис. 20, можно выразить через
Из формулы (2) выразим перпендикулярную составляющую скорости:
Параллельную составляющую скорости
Подставив вместо Т правую часть выражения (2), получим
Таким образом, модуль скорости электрона
Убедимся в том, что правая часть равенства дает единицу скорости (м/с). Для этого заметим, что R и h имеют одинаковую единицу — метр (м). Поэтому в квадратных скобках мы поставим только одну из величин (например, R):
Произведем вычисления:
Пример 33. Альфа-частица прошла ускоряющую разность потенциалов U= 104 В и влетела в скрещенные под прямым углом электрическое (Е= кВ/м) и магнитное (В = 0,1 Тл) поля. Найти отношение заряда альфа - частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории. Решение. Для того чтобы найти отношение заряда Q альфа - частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частицы:
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.016 с.) |

 ,
,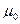 - магнитная постоянная;
- магнитная постоянная;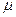 -магнитная проницаемость среды.
-магнитная проницаемость среды.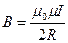 ;
;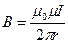 ;
;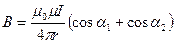 ,
,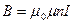 ,
,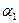 и
и  — углы между отрезком проводника и
— углы между отрезком проводника и ,
,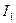 и
и  .
.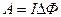 ,
,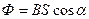 ,
, — угол между вектором
— угол между вектором 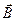 и
и ,
,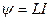 ,
, .
.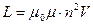 ,
, n — число витков на единицу длины соленоида
n — число витков на единицу длины соленоида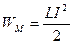
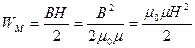
 Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой из зарядов, например Q1, находился в равновесии. Заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис. 6):
Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой из зарядов, например Q1, находился в равновесии. Заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис. 6):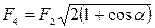
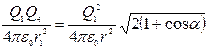 ,
,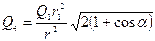 . (2)
. (2)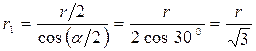 , cos α = cos 600 = 1/2.
, cos α = cos 600 = 1/2. .
.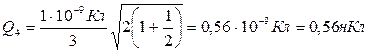
 9нКл и
9нКл и 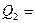 -7 нКл расположены в вершинах равностороннего треугольника со стороной
-7 нКл расположены в вершинах равностороннего треугольника со стороной 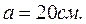 Определить напряженность и потенциал электрического поля в третьей вершине треугольника.
Определить напряженность и потенциал электрического поля в третьей вершине треугольника. и
и  полей, создаваемых зарядами
полей, создаваемых зарядами 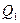 и
и 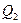 соответственно:
соответственно: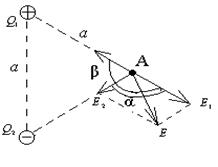

 и
и  :
: . (1)
. (1) Напряженность электрического поля точечного заряда выражается формулой
Напряженность электрического поля точечного заряда выражается формулой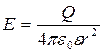 (2)
(2) - электрическая постоянная;
- электрическая постоянная;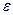 - диэлектрическая проницаемость среды;
- диэлектрическая проницаемость среды;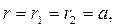 то имеем:
то имеем: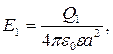
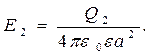 (3)
(3)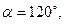 преобразуем:
преобразуем:
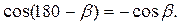 (4)
(4)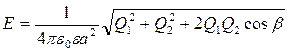 (5)
(5)
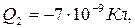
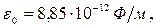
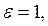
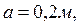
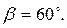
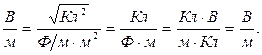
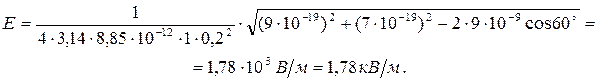
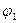 и
и  полей, создаваемых зарядами
полей, создаваемых зарядами 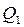 и
и 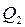 соответственно:
соответственно: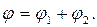 (6)
(6)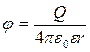 (7)
(7) В формуле (7) обозначения те же, что и в формуле (2). Подставив формулу (7) в (6) и учитывая, что
В формуле (7) обозначения те же, что и в формуле (2). Подставив формулу (7) в (6) и учитывая, что  . (8)
. (8)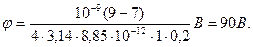
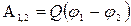 .
.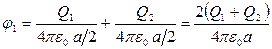 ;
;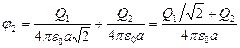 .
.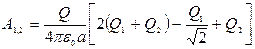
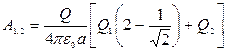 .
.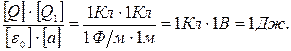
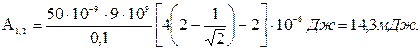

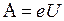 . (1)
. (1) , (2)
, (2)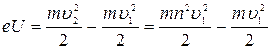 ,
,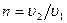 .
.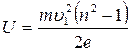 .
. .
.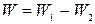 , (1)
, (1)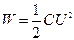 , (2)
, (2)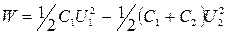 , (3)
, (3) . (4)
. (4)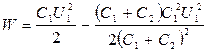
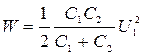 .
. .
.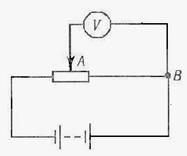 внутренним сопротивлением Ri = 50 Ом. Определить: 1) показание вольтметра сопротивлением Rv = 500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра; 2) разность потенциалов между теми же точками потенциометра при отключении вольтметра.
внутренним сопротивлением Ri = 50 Ом. Определить: 1) показание вольтметра сопротивлением Rv = 500 Ом, соединенного с одной из клемм потенциометра и подвижным контактом, установленным посередине потенциометра; 2) разность потенциалов между теми же точками потенциометра при отключении вольтметра. Решение. 1. Показание вольтметра, подключенного к точкам А и В (рис. 9), определим по формуле:
Решение. 1. Показание вольтметра, подключенного к точкам А и В (рис. 9), определим по формуле: ,
,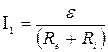 , (1)
, (1)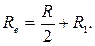 (2)
(2) , откуда
, откуда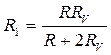 .
.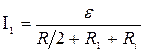 .
.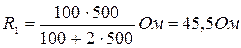 ;
;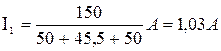 ;
; .
.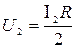 , (3)
, (3)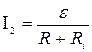 .
.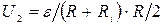 .
. .
.
 Решение. Закон Джоуля-Ленца в виде
Решение. Закон Джоуля-Ленца в виде 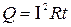 справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде:
справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде: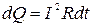 . (1)
. (1)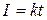 , (2)
, (2) .
.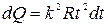 . (3)
. (3)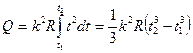 .
.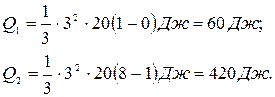
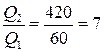 ,
, Решение. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукции B1 и B2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
Решение. Для нахождения магнитной индукции В в точке А воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитных индукции B1 и B2 полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: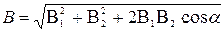 , (1)
, (1)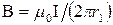 ;
; 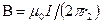
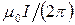 за знак корня, получаем
за знак корня, получаем
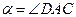 (как углы c соответственно перпендикулярными сторонами), по теореме косинусов запишем
(как углы c соответственно перпендикулярными сторонами), по теореме косинусов запишем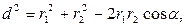

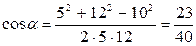 .
.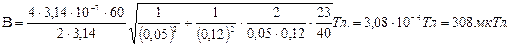
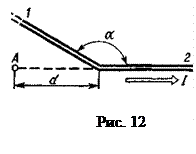
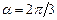 . Определить магнитную индукцию В в точке А (рис. 12). Расстояние d = 5 см.
. Определить магнитную индукцию В в точке А (рис. 12). Расстояние d = 5 см.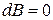 ([dlr])=0.
([dlr])=0. ,
, В нашем случае
В нашем случае 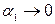 (провод длинный),
(провод длинный), 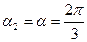 (cosα2=cos(2π/3)=-1/2). Расстояние
(cosα2=cos(2π/3)=-1/2). Расстояние 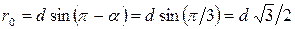 Тогда магнитная индукция
Тогда магнитная индукция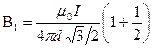
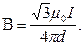
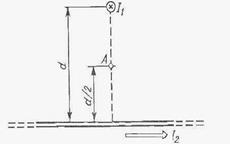

 Пример 27. Два бесконечно длинных провода скрещены под прямым углом (рис. 14). По проводам текут токи I1 = 80 А и I2=60 А. Расстояние d, между проводами равно 10 см. Определить магнитную индукцию В в точке A, одинаково удаленной от обоих проводов.
Пример 27. Два бесконечно длинных провода скрещены под прямым углом (рис. 14). По проводам текут токи I1 = 80 А и I2=60 А. Расстояние d, между проводами равно 10 см. Определить магнитную индукцию В в точке A, одинаково удаленной от обоих проводов.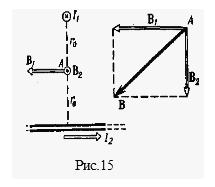 Решение. В соответствии с принципом суперпозиции магнитных полей магнитная индукция В поля, создаваемого токами I1и I2, определяется выражением
Решение. В соответствии с принципом суперпозиции магнитных полей магнитная индукция В поля, создаваемого токами I1и I2, определяется выражением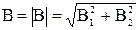 ,
,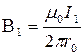 и
и 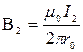
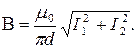
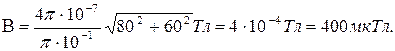
 . В нашем случае провод можно разбить на три части (рис. 17): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2)радиуса R. Тогда
. В нашем случае провод можно разбить на три части (рис. 17): два прямолинейных провода (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2)радиуса R. Тогда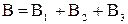
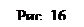

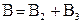
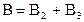
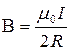
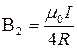 .
.
 (cos α2=-1).Тогда
(cos α2=-1).Тогда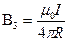
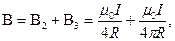
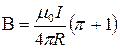
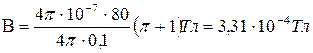
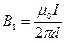 (1)
(1)
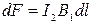
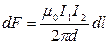
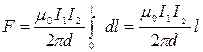
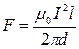
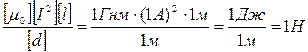
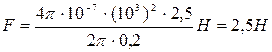 '
'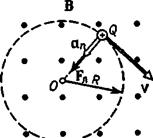 Решение. Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитной индукции v
Решение. Движение заряженной частицы в однородном магнитном поле будет происходить по окружности только в том случае, когда частица влетит в магнитное поле перпендикулярно линиям магнитной индукции v  В. Так как сила Лоренца перпендикулярна вектору v, то она сообщит частице (протону) нормальное ускорение аn.
В. Так как сила Лоренца перпендикулярна вектору v, то она сообщит частице (протону) нормальное ускорение аn. Согласно второму закону Ньютона,
Согласно второму закону Ньютона, (1)
(1)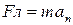 (2)
(2)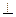 В и sin α = 1, тогда F л= Q v В. Так как нормальное ускорение аn= v2/R, то выражение (2) перепишем следующим образом:
В и sin α = 1, тогда F л= Q v В. Так как нормальное ускорение аn= v2/R, то выражение (2) перепишем следующим образом: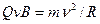
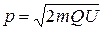 и подставим его в формулу (3):
и подставим его в формулу (3):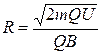
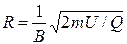
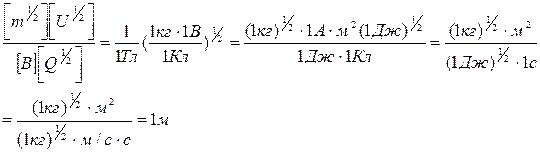
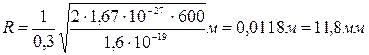
 Пример 31. Электрон, влетев в однородное магнитное поле (В= 0,2 Тл), стал двигаться по окружности радиуса R=5см. Определить магнитный момент рт эквивалентного кругового тока.
Пример 31. Электрон, влетев в однородное магнитное поле (В= 0,2 Тл), стал двигаться по окружности радиуса R=5см. Определить магнитный момент рт эквивалентного кругового тока. Решение. Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. На
Решение. Электрон начинает двигаться по окружности, если он влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. На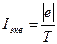
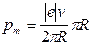
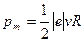 (3)
(3)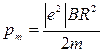
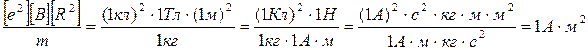
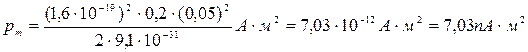
 ). Скорость v
). Скорость v  ) (в отсутствие параллельной составляющей (v = 0) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям). Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении со скоростью v и равномерном движении по окружности со скоростью v
) (в отсутствие параллельной составляющей (v = 0) движение электрона происходило бы по окружности в плоскости, перпендикулярной магнитным силовым линиям). Таким образом, электрон будет участвовать одновременно в двух движениях: равномерном перемещении со скоростью v и равномерном движении по окружности со скоростью v  . Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение ап= v 2
. Для этого воспользуемся тем, что сила Лоренца сообщает электрону нормальное ускорение ап= v 2 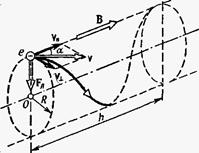 написать
написать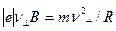
 Сократив (2) на v
Сократив (2) на v 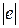 B)
B)
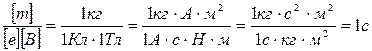
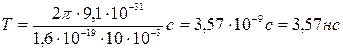
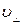 и
и 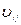 :
: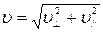
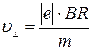
 , откуда
, откуда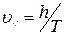 .
.