
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле прямолинейного проводника с током.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
M µ I r A C r0 В на нас N Найдём индукцию в точке А, создаваемую проводником на расстоянии. По з-ну БСЛ для элемента имеем: Рассмотрим частный случай: Пусть есть бесконечный проводник: ф1=00, ф2=1800
Определение единицы силы тока-Ампера
 , ,  , , 
проводника, то получаем:
Если токи в одном направлении,то они притягиваются
Выражение для силы F(*) позволяет определить единицу силы тока в СИ. Ампер равен силе неизменяющегося тока, который при прохождении по 2-ум параллельным проводникам бесконечной длины и ничтожно малой площадью кругового поперечного сечения, расположенного в вакууме на расстоянии 1 м друг от друга вызывал бы на каждом участке проводника длиной 1 м силу взаимодействия 2•10-7 Н/м. Из последнего определения вытекает магнитная постоянная m0; m=1; I1= I 2=1А; l=1;x=1. Подставим в формулу(*) 2•10-7=m0 *1*2*1*1*1/4π*1, получаем m0 =4•10-7 Гн/м
поля с радиусом R. По з-ну БСЛ им для эл-та тока Idl:
Напряж магнитного поля в центре кругового витка:

силы тока I на площадь витка S: Pµ=IS, [Pµ]=А*м2. Pµ-вектор направлен как и магнитная индукция витка В Закон полного тока Закон полного тока(теорема о циркуляции вектора магнитной индукции):циркуляция вдоль замкнутого контура вектора магнитной индукции в вакууме равна произведению магнитной постояннойm0 на алгебраическую сумму токовохватываемых этим контуром:
 , , 
Теорема о циркуляции вектора магнитной индукции есть следствие з-на БСЛ, но она допуск обобщение на поля и люб среды. При таком обобщении эта теорема – одно из обобщ электродинамики Максвелла:
Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида. Применим теорему о циркуляции вектора магнитной индукции. Для вычисления Тороида и длинного соленоида. Тороид – каркас с формой бублика с навитым на него витками проводника по которому течет ток I. Соленоид – цилиндрическая катушка из большого числа намотанного в плотную проводника с током I. Тороид: За контур L возьмем окружность радиуса r так, что контур внутри тороида. Тороид можно рассмотреть как систему последовательно соединенных r круговых токов одинакового радиуса и нанизанных на общую o R круговую ось радиуса R. По теореме циркуляции имеем т.к. контур L проходит внутри тороида, то он охватывает ток равный 2πRnI, где n – число витков на единицу длины – плотность витков. Из симметрии вектор В в каждой точке напр по касй к L, тогда Соленоид: есть тороид бесконечно большого радиуса, т.е R→∞ N Bсол=μ0μnI – магнитное поле соленоида
l
Сила Лоренца Сила Ампера действует на проводник с током, но токи направленное упорядоченное движение зарядов. Тогда сила Ампера должна действовать и на отдельные движущиеся заряды. Найдем исходя из силы Ампера выражение для силы действующей на заряд q движущейся со скоростью B dl Рассмотрим проводник длиной dl и площадью поперечного сечения S в S магнитном поле с индукцией. Пусть ток в проводнике – I. Заряд q
В и нта. Если вращать рукоятку правого винта от первого вектора υ ко α второму вектору В на кратчайший угол α, то поступательное движение винта укажет направление силы Лоренца при положительном заряде: Магнитное взаимод проводника с током и действ магн поля на движ-ся зар предст собой чисто релитивиский эффект. В сист Гаусса выраж для силы:
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.221.126 (0.009 с.) |

 ,
,  . По принципу суперпозиции проинтегрируем последнее выражение:
. По принципу суперпозиции проинтегрируем последнее выражение:  . С учётом
. С учётом  получаем:
получаем:  . Направление в-ра В опред прав правого винта.
. Направление в-ра В опред прав правого винта. ,
, 
 . Проинтегрируем по длине
. Проинтегрируем по длине (*)
(*)
 , r=R=const
, r=R=const .
.
 . Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током.
. Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током. . Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.
. Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.
 . Ок-но имеем: В2πr=μ02πRnI =>
. Ок-но имеем: В2πr=μ02πRnI =>  . Если внутри тороида среда с магнитной проницаемостью μ, тогда
. Если внутри тороида среда с магнитной проницаемостью μ, тогда 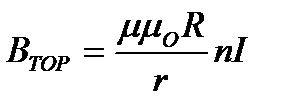 .
.
 , где N – число витков; l – длина соленоида
, где N – число витков; l – длина соленоида со стороны магнитного поля с индукцией - сила Лоренца.
со стороны магнитного поля с индукцией - сила Лоренца.
 со скор
со скор  , а
, а  . Покажем, что эл тока Idl будет э I эквивалентен: qdn
. Покажем, что эл тока Idl будет э I эквивалентен: qdn  , Id
, Id  =qdn
=qdn  , где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d
, где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d  , тогда Id
, тогда Id  Sdl => Id
Sdl => Id  dV, а
dV, а  – сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:
– сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:  – сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в
– сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в
 К которой лежит
К которой лежит  . Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью
. Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью  . Виды траектории зар под действ силы Лоренца: 1. прямая линия
. Виды траектории зар под действ силы Лоренца: 1. прямая линия  ; 2. окружность
; 2. окружность  ; 3. цилиндрическая спираль (нарезка винта)
; 3. цилиндрическая спираль (нарезка винта)  .
. ,
,  - в сист Гаусса действ магн поля оч мало (много меньш эл-ского).
- в сист Гаусса действ магн поля оч мало (много меньш эл-ского).


