
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрический заряд. Дискретность заряда. Закон Кулона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электрический заряд. Дискретность заряда. Закон Кулона. Из опытов следует, что тела, например при трении, способны наэлектризовываться, т.е. приобретать Эл/з. наэл тела взаим между сабой. Сущ. два вида Эл/з, условно называемые «+» и «-». Из опытов следует, что Эл/з дискретен, т.е. Эл/з q тела: q = Диэлектрическая проницаемость показывает во сколько раз сила взаимодействия задов в среде меньше, чем в вакууме.
Напряженность Эл.п. Принцип суперпозиции. Взаимодействие между покоящимися зар. осуществляется посредством Эл.п. (электро-статического поля). понятие Эл.п. ввел Фарадей. Неподвижный Эл.зар. изменяет свойство пространства и создает Эл.п. Оно проявляется по действию на пробный зар. Отношение силы действующей со стороны поля на пробный зар. не зависит от величины этого зар. и может хар-ть само Эл.п., тогда приходим к характеристике поля – напряженности: Эл.п. эсть векторная силовая характеристика поля = отношению силы, действующей на зар. со стороны поля,к зар., т.е.:
Если известна Е, то сила со стороны поля действующая на зар. q =: Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.:
Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.
Если непрерывно распределенный зар. т.е.:
Законы Ома и Джоуля - Ленца в дифференциальной форме Из Опыта известно что сопротивление R цилиндрического проводника длиною l и площадью поперечного сечения S:
ρ = ρ Это эквивалентно выражению: ј =σE
Закон Джоуля-Ленца (1841-1842) При прохождении заряда q по участку цепи I=q/t, q=It, совершается работа A=qU=IUt Если проводник неподвижный и отсуствует хим.реакции, то работа А идёт на увеличение внутренней энергии проводника: Q=IUt. Чаще в такой форме Q= Если ток переменный I=I(t): dQ= Получим теперь закон в диф.форме(локальной форме): Объёмной плотностью тепловой мощности называется тепловая энергия в единице объёма за единицу времени: Поскольку Q=IUt то получим: ω =
ω=σ
Закон Био-Савара-Лапласа З-н БСВ даёт выражение для магнитной индукции d
Id | µ |α | | | d З-н БСЛ: µ0 — магнитная постоянная=4π·10-7 Гн/м; µ — магнитная проницаемость среды Модуль индукции |dB|: З-н БСЛ для напряжённости З-н БСЛ совместно с принципом суперпозиции допускает в принципе вычисление магнитных полей любой конфигурации токов.
Закон полного тока Закон полного тока(теорема о циркуляции вектора магнитной индукции):циркуляция вдоль замкнутого контура вектора магнитной индукции в вакууме равна произведению магнитной постояннойm0 на алгебраическую сумму токовохватываемых этим контуром:
 , , 
Теорема о циркуляции вектора магнитной индукции есть следствие з-на БСЛ, но она допуск обобщение на поля и люб среды. При таком обобщении эта теорема – одно из обобщ электродинамики Максвелла:
Сила Лоренца Сила Ампера действует на проводник с током, но токи направленное упорядоченное движение зарядов. Тогда сила Ампера должна действовать и на отдельные движущиеся заряды. Найдем исходя из силы Ампера выражение для силы действующей на заряд q движущейся со скоростью B dl Рассмотрим проводник длиной dl и площадью поперечного сечения S в S магнитном поле с индукцией. Пусть ток в проводнике – I. Заряд q
В и нта. Если вращать рукоятку правого винта от первого вектора υ ко α второму вектору В на кратчайший угол α, то поступательное движение винта укажет направление силы Лоренца при положительном заряде: Магнитное взаимод проводника с током и действ магн поля на движ-ся зар предст собой чисто релитивиский эффект. В сист Гаусса выраж для силы:
Дифракция света - явление отклонения света от прямолинейного распространения, проявляющегося в огибании светом препятствий и захождении света в область геометрической тени при прохождении отверстия. Размеры препятствий (отверстий) соизмеримы с длиной волны. Различают дифр-ю Фраунгофера и Френеля в сходящихся лучах. Начальные закономерности устанавливаются с помощью принципа Гюгенса-Френеля, по которому любая точка фронта волны, до которой дошли колебания является источником вторичных волн и поверхность, которую огибают эти вторичные волны есть фронтовой фронт. 1
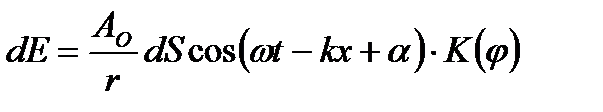
K( Дифракционная решётка. Простейшая дифракционная решётка представляет собой систему параллельных щелей, разделённых одинаковыми непрозрачными промежутками.
На Д.Р. имеют место два явления: дифракция света на каждой щели и интерференция света от всех щелей. Условие, определяющее главные максимумы интенсивности для дифракционной решётки, имеет вид: dsinφ=κλ, где к=0, ±1,±2…. к-порядок спектра, φ-угол дифракции, λ-длина волны света. Максимум нулевого порядка один, а максимумов 1-ого,2-ого.3-ого и т.д. порядок по два. Положения главных макс, кроме нулевого, зависит от длины волны. Поэтому при пропускании через решётку белого света все макс, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращён к центру дифракционной картинки. Т.о. дифракционная решётка является спектральным прибором. Для нулевого порядка для любой длины волны дифракционный угол φ=0. Поэтому нулевом порядке белый свет не разлагается в спектр. Хар-ки решётки: 1. угловая дисперсия Д – производная от угла диф-ции
Принцип голографии. Голография-безлинзовое воспроизведение пространственного изображения предмета, полученное путём восстановления всего волнового фронта. Денис Габор-1971г.При обычном фотографировании предметов на фотопластинке регистрируется только интенсивность света рассматриваемого объекта
Первые лазерные диаграмы-1963г.Амплитудная и фазовая информации заключены в соотношении для двух интерферирующих волн: Схема Денисюка:
Для восстановления предметной волны необходимо голограму осветить опорной волной, т.е. лазером и восстанавливается полный волновой фронт. Двойное лучепреломление. При прохождении света ч/з прозрачные кристаллы некубической симметрии наблюдается двойное лучепреломление состоящее в том, что луч в кристалле разделяется на луч обыкновенный (о) и необыкновенный (е), кот распространяются в общем случае с разными скоростями и в различных направлениях лучи о и е поляризованы в 2 взаимно перпендикулярных плоскостях. е
о
кристаллы, для которых имеется единственное направление, вдоль кот происх двойное лучепреломление, наз одноосным. Направление, вдоль кот не происходит двойное лучепреломление, наз оптической осью кристалла. Кристаллы, имеющие 2 направления, вдоль кот не происходит двойное лучепреломление, наз двуосными, у них оба луча е. Для е не выполняется закон преломления: Двойное лучепреломление объясняется анизотропией кристалла. Показатель преломления: Различают ε таких кристаллов в направлении перпендикулярном и параллельном оптич оси. Волновая поверхность о - сфера, а для е - элепсоид. 59° Поляроиды и поляризационные призмы.
Способы получения поляризованного света: 1. Лазер 2. Рассеяние света на мелких частицах (пыли) 3. Использользуется закона Брюстера. Стопа Столетова – совокупность стеклянных пластинок, наклоненных к падающему лучу под углом Брюстера. 4. Призма Николя использует явление двойного лучепреломления. Николь представляет собой двойную призму, вырезанную из кристалла исландского шпата. 5. Для поляризации используют явление дихроизма, т.е. различную степень поглощения нормального и естественного лучей. Например обыкновенный луч в кристалле турмалина поглощается на расстоянии 1мм. Поляроиды – поляризаторы с большой поверхностью. Их получают путем нанесения на целлоидную пленку сильно дихроичного герапатита. Оптически активные вещества – вещества, поворачивающие плоскость поляризации (кварц, растворы сахара, жидкие кристаллы).Угол поворота плоскости поляризации для твердых тел φ = α∙ l, где l – длина пути, которую прошел луч; α - коэффициент удельного вращения; φ – угол поворота в растворах.
В растворах угол поворота φ= α∙с∙ l,где с – концентрация раствора.
Эффекты Пельтье и Томсона. Пельтье: «В контакте, через кот прох ток, помимо тепла Джоуля – Ленца происходит выделение или поглощение тепла, и контакт нагрев или охлажд». Эффект Пельтье обратен эффекту Зеебека. Тепло Пельтье пропорц. полному заряду, прошедш. через спаи: Томсона: «при пропускании тока через однородн. неравн. нагретый проводник, в нём выделяется или поглощается добавочное кол-во тепла - тепло Томсона». Эффект Томсона есть эффект Пельтье, когда неоднородность обусловл. не различием хим. состава проводн., а обусловлено разл. темпер., при этом происходит диффузия из нагретой части в холодную: Электрический заряд. Дискретность заряда. Закон Кулона. Из опытов следует, что тела, например при трении, способны наэлектризовываться, т.е. приобретать Эл/з. наэл тела взаим между сабой. Сущ. два вида Эл/з, условно называемые «+» и «-». Из опытов следует, что Эл/з дискретен, т.е. Эл/з q тела: q = Диэлектрическая проницаемость показывает во сколько раз сила взаимодействия задов в среде меньше, чем в вакууме.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.196.222 (0.016 с.) |

 Nе, N=0,1,2,3… е- элементарный зар. е=1,6*10ˉ19Кл. Носителем «-» Элем/з явл. электрон, «+» зар. ядро атома водорода, протон или позитрон. Единицей измерения Эл/з в СИ Кулон (Кл), он определяется из силы тока
Nе, N=0,1,2,3… е- элементарный зар. е=1,6*10ˉ19Кл. Носителем «-» Элем/з явл. электрон, «+» зар. ядро атома водорода, протон или позитрон. Единицей измерения Эл/з в СИ Кулон (Кл), он определяется из силы тока  ⇒ q=It 1Кл=1А*1с. Кулон –зар. проходящий через поперечное сечение проводника за 1с при силе тока в проводнике 1А. Для Э/з споведл з-н сохр: «суммарный заряд электрич изолир сист сохран во врем».
⇒ q=It 1Кл=1А*1с. Кулон –зар. проходящий через поперечное сечение проводника за 1с при силе тока в проводнике 1А. Для Э/з споведл з-н сохр: «суммарный заряд электрич изолир сист сохран во врем».  . Система электрически изолированная, если через ее границу не проходят зар. тела. Электростатика изучает з-ны взаимодействия неподвижных зар. Основной З. электростатики – З.Кулона (1785): «сила взаимод 2-ух точечных неподвижных Э/л зар в вакууме прямопропорц произвед модулей этих зарядов и обратно пропорц квадр раст между зар».
. Система электрически изолированная, если через ее границу не проходят зар. тела. Электростатика изучает з-ны взаимодействия неподвижных зар. Основной З. электростатики – З.Кулона (1785): «сила взаимод 2-ух точечных неподвижных Э/л зар в вакууме прямопропорц произвед модулей этих зарядов и обратно пропорц квадр раст между зар».  . Сила направленная по прямой, соединяющих зар. так, что одноименные зар. отталкиваются, а разноименные притягиваются. Зар. точечный, если размеры зар. тел малы по сравнению с расстоянием между ними. к - к-т пропорциональности
. Сила направленная по прямой, соединяющих зар. так, что одноименные зар. отталкиваются, а разноименные притягиваются. Зар. точечный, если размеры зар. тел малы по сравнению с расстоянием между ними. к - к-т пропорциональности  ,
,  - электрическая постоянная,
- электрическая постоянная,  . εвак=1, εстекла=4/3, εводы=81. З.Кулона в векторном виде:
. εвак=1, εстекла=4/3, εводы=81. З.Кулона в векторном виде:

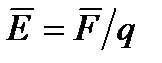 , q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар.
, q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар. 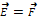 , когда q=+1. Единицы измерения напряжения
, когда q=+1. Единицы измерения напряжения  ,
,  . Найдем напряжение поля точечного зар. q, находящейся в точке. Хар. вектором
. Найдем напряжение поля точечного зар. q, находящейся в точке. Хар. вектором  в среде, по З.Кулона можем записать
в среде, по З.Кулона можем записать
 ,
,  - созд. точечный зар.
- созд. точечный зар.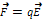
 , помножим на
, помножим на 
 … т.е.
… т.е.  - принцип суперпозиции.
- принцип суперпозиции.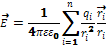

 .Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей. Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке. Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в
.Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей. Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке. Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в  . Густота силовых линий,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально
. Густота силовых линий,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально  . По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:
. По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:

 ρ
ρ  S,
S, 

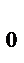 (1+αtoC), I=
(1+αtoC), I=  , I=
, I=  ∙
∙  ∙S │:S,
∙S │:S,  =
= 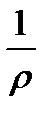 ∙
∙ 
 - это закон Ома в диф.форме; если присутствуют сторонние силы:
- это закон Ома в диф.форме; если присутствуют сторонние силы: 
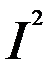 Rt.
Rt. (t)Rdt
(t)Rdt
 =
=  = јE
= јE – закон Джоуля-Ленца в диф.форме
– закон Джоуля-Ленца в диф.форме ,т.к E=ј/σ, ω= ρ
,т.к E=ј/σ, ω= ρ 
 , создаваемой элементом I d
, создаваемой элементом I d 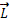 в точке, характеризуемой радиус-вектором
в точке, характеризуемой радиус-вектором  , проведённым из элемента проводника d
, проведённым из элемента проводника d 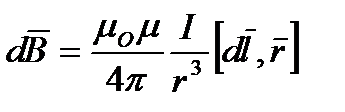
 . Наряду с магнитной индукцией, можно характеризовать напряжённость магнитного поля. Дл изотропного случая:
. Наряду с магнитной индукцией, можно характеризовать напряжённость магнитного поля. Дл изотропного случая: 
 принимает вид:
принимает вид: 
 . Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током.
. Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током. . Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.
. Т о цирк в-ра магн инд позвол магн поля различных конструкций токов. со стороны магнитного поля с индукцией - сила Лоренца.
со стороны магнитного поля с индукцией - сила Лоренца.
 со скор
со скор  , а
, а  . Покажем, что эл тока Idl будет э I эквивалентен: qdn
. Покажем, что эл тока Idl будет э I эквивалентен: qdn  , Id
, Id  =qdn
=qdn  , где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d
, где q – заряд; dn – число зарядов; υ – скорость их движения. Действительно сила постоянного тока I=jS, где S – площадь поперечного сечения; j – плотность тока. Умножим на d  , тогда Id
, тогда Id  Sdl => Id
Sdl => Id  dV, а
dV, а  – сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:
– сила действующая на рассмотриваемый проводник в котором число зарядов dn, тогда сила действующая на один заряд:  – сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в
– сила Лоренца, знак q учитывается. Абсолютны знак силы Лоренца определяется согласно правилу векторного произведения: сила Fл перпендикулярна площади, в
 К которой лежит
К которой лежит  . Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью
. Выражение для силы Лоренца зависит от выбора системы отсчета: если заряд движется со скоростью  . Виды траектории зар под действ силы Лоренца: 1. прямая линия
. Виды траектории зар под действ силы Лоренца: 1. прямая линия  ; 2. окружность
; 2. окружность  ; 3. цилиндрическая спираль (нарезка винта)
; 3. цилиндрическая спираль (нарезка винта)  .
. ,
,  - в сист Гаусса действ магн поля оч мало (много меньш эл-ского).
- в сист Гаусса действ магн поля оч мало (много меньш эл-ского). M
M
 ) – некот ф-ция кот зависит от угла
) – некот ф-ция кот зависит от угла  ;
;  - соотн принципа Гюйгенса – Френеля.
- соотн принципа Гюйгенса – Френеля.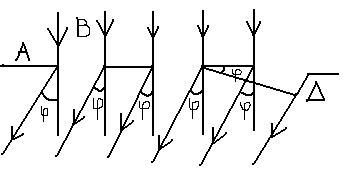 d=a+b-постоянная дифракционной решетки.
d=a+b-постоянная дифракционной решетки.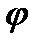 по длине вел-ны
по длине вел-ны  :
:  - хар-ет степень растянутости спектра в области данной длины волны; 2. разрешающая сила решётки:
- хар-ет степень растянутости спектра в области данной длины волны; 2. разрешающая сила решётки: 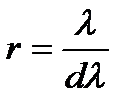 - показ какие спектр линии с малой разницей длин волн
- показ какие спектр линии с малой разницей длин волн  решётки может разрешать, т.е. позв наблюд эти линии раздельно. Разреш силу можно предст: r=mNo. m – порядок спектра, No – общее число штрихов решётки.
решётки может разрешать, т.е. позв наблюд эти линии раздельно. Разреш силу можно предст: r=mNo. m – порядок спектра, No – общее число штрихов решётки. ,но светов. волна характеризуется ещё фазой.Габор предложил регестрировать на фотопластинке не только квадраты амплитуд, но и их фазы,используя явление дифракции-интерференции.
,но светов. волна характеризуется ещё фазой.Габор предложил регестрировать на фотопластинке не только квадраты амплитуд, но и их фазы,используя явление дифракции-интерференции.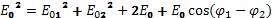 .Для регистрации фазовой и амплитудной информаций необходимо кроме волны,идущей от предмета (предметной волны),ещё иметь когерентную с ней волну,наз. опорной волной.
.Для регистрации фазовой и амплитудной информаций необходимо кроме волны,идущей от предмета (предметной волны),ещё иметь когерентную с ней волну,наз. опорной волной.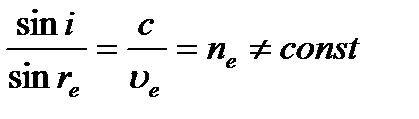

 Поляризатор Р – прибор для получения поляризованного света. Анализатор А – прибор для анализа поляризованного света.
Поляризатор Р – прибор для получения поляризованного света. Анализатор А – прибор для анализа поляризованного света.
 - сависит от напр тока, т.к. I в 1-ой степени, П – к-т Пельтье. Тепло Джоуля - Ленца:
- сависит от напр тока, т.к. I в 1-ой степени, П – к-т Пельтье. Тепло Джоуля - Ленца:  - не зависит от напр тока. Для измер
- не зависит от напр тока. Для измер 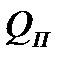 берут очень толстые проводники и меняют напр тока, уменьш и увелич тепла. Тепло Пельтье объясняется наличием контактной разности потенциалов, она либо ускоряет движение электронов, либо замедляет. Эффект Пельтье использ. для устройства термоэлектр. холодильников (Т= - 30 - + 300С).
берут очень толстые проводники и меняют напр тока, уменьш и увелич тепла. Тепло Пельтье объясняется наличием контактной разности потенциалов, она либо ускоряет движение электронов, либо замедляет. Эффект Пельтье использ. для устройства термоэлектр. холодильников (Т= - 30 - + 300С).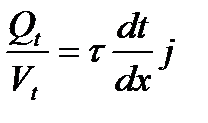 , где
, где  - плотность тока;
- плотность тока; 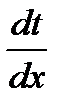 - град. темп.
- град. темп.


