
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическая цепь и ее элементы.Содержание книги
Поиск на нашем сайте Электрическая цепь и ее элементы. Реальная электрическая цепь - совокупность устройств, предназначенных для передачи, распределения и преобразования энергии. Содержит источники электрической энергии, приемники электрической энергии, измерительные приборы, коммутационную аппаратуру, соединительные линии и провода. Электрическая цепь представляет собойсовокупность связанных определенным образом источников, потребителей (или соответственно активных и пассивных элементов) и преобразователей электрической энергии. Цепь называют пассивной, если она состоит только из пассивных элементов, и активной, если в ней также содержатся активные элементы. Источником электрической энергии называют элемент электрической цепи, осуществляющий преобразование энергии неэлектрического вида в электрическую. Потребителем электрической энергии называют элемент электрической цепи, преобразующий электрическую энергию в неэлектрическую. Преобразователем электрической энергии называют устройство, изменяющее величину и форму электрической энергии. Для того чтобы выполнить расчет, необходимо каждое электротехническое устройство представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности идеализированных элементов(резистор, конденсатор, катушка индуктивности). Напряжение: Ток: Зависимость между током и напряжением на элементе цепи называется вольт-амперной характеристикой (ВАХ) элемента, которая обычно изображается графически. В качестве потребителя в теории электрических цепей постоянного тока выступает резистор, характеризующийся сопротивлением (R), для которого справедлив закон Ома:
Проводимость: Источники энергии моделируются с помощью источника ЭДС (Е), или источника напряжения, и источника тока (J). В большинстве случаев с увеличением тока напряжение источника уменьшается. Идеализированный источник напряжения – это элемент цепи, напряжение которого не зависит от тока и является заданной постоянной величиной. В действительности мы имеем дело с реальными источниками напряжения, которые отличаются от идеальных источников тем, что их напряжение с ростом потребляемого тока уменьшается. Любой реальный источник при сопротивлении нагрузки R >> R 0 может быть приведен к идеализированному следующим образом:
Идеализированный источник тока – это элемент цепи, ток которого не зависит от напряжения и является заданной постоянной величиной. У реального источника тока с ростом напряжения вырабатываемый ток уменьшается.Любой реальный источник тока может быть приведен к идеализированному следующим образом:
Обобщенный закон Ома.
Рассмотрим закон Ома для участка цепи, содержащего активные и пассивные элементы
Объединив эти две формулы, получаем:
Отсюда ток Аналогияно:
Объединив эти две формулы в одну, получим:
Обобщенный закон Ома для ветви, содержащей источник тока: Для содействующего источника тока
Для противодействующего источника тока
Объединенная форма обобщенного закона Ома для ветвей, содержащих источник тока:
где верхний знак соответствуют схеме, на которой U J и J сонаправлены.
Законы Кирхгофа. I закон Кирхгофа (для токов): алгебраическая сумма токов в узле равна нулю, или сумма притекающих и сумма истекающих токов одинаковы. Как правило, при суммировании притекающие токи берутся со знаком «+», а истекающие – со знаком «–». II закон Кирхгофа (для напряжений): алгебраическая сумма ЭДС всех источников, встречающихся при обходе контура, равна алгебраической сумме напряжений на всех потребителях. В алгебраической форме В сумму со знаком «+» входят ЭДС содействующих источников и со знаком «–» ЭДС противодействующих источников. При суммировании напряжений потребителей со знаком «+» берутся напряжения на всех потребителях, токи которых направлены согласно с обходом контура, и со знаком «–» берутся напряжения всех остальных потребителей. 8) Эквивалентные преобразования пассивных электрических цепей. Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем. При последовательном соединении роль эквивалентного сопротивления играет сумма сопротивлений всех потребителей (рис. 1.11.).
При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
Это следует из I закона Кирхгофа:
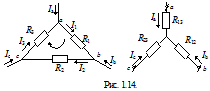
9-10) Эквивалентное преобразование «Звезда – треугольник»
В узлах a, b, c и треугольник, и звезда на рис. 1.14. соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены. Выразим U abтреугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.
Заменим в первом уравнении токи I 3 и I 2на соответствующие выражения:
Теперь получим выражение для этого же напряжения при соединении потребителей звездой:
Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника. Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений через проводимости:
или через сопротивления:
Баланс мощности. Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию:
По обобщенному закону Ома.
Выражения, записанные для ветви с источником напряжения, справедливы и для ветви с источником тока, если произвести подстановку Отсюда следует закон сохранения энергии, согласно которому алгебраическая сумма мощностей, подводимых ко всем ветвям разветвленной электрической цепи, равна нулю:
Существует еще одна форма записи баланса мощности:
В левой части суммируются мощности источников энергии, а в правой – мощности, преобразованные в потребителях в тепло. Мощности источников, отдающих энергию, берутся со знаком «+», а работающих в режиме потребителей – со знаком «–».
Метод уравнений Кирхгофа. 1. Обозначить токи ветвей и произвольно выбрать их положительное направление. 2. Произвольно выбрать опорный узел и совокупность p = m – n + 1 независимых контуров. 3. Для всех узлов, кроме опорного, составить уравнения по I закону Кирхгофа. Таких уравнений должно быть (n – 1). 4. Для каждого выбранного контура составить уравнения по II закону Кирхгофа. Таких уравнений должно быть p. 5. Система m уравнений Кирхгофа с m неизвестными токами решается совместно и определяются численные значения токов. 6. Если необходимо, рассчитать с помощью обобщенного закона Ома напряжения ветвей или разность потенциалов узлов. 7. Проверить правильность расчета с помощью баланса мощности. Если в цепи есть q источников тока и контуры выбирать таким образом, чтобы каждый источник тока вошел только в один контур, то количество уравнений по II закону Кирхгофа можно уменьшить до m – n + 1 – q. Метод Контурных Токов За искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по II закону Кирхгофа, т.е. По найденным контурным токам при помощи I закона Кирхгофа определяются токи ветвей. Таким образом, методика расчета цепи постоянного тока методом контурных токов следующая: 1. Обозначить все токи ветвей и их положительное направление. 2. Произвольно выбрать совокупность p независимых контуров, нанести на схему положительное направление контурных токов, протекающих в выбранных контурах. 3. Определить собственные, общие сопротивления и контурные ЭДС и подставить их в систему уравнений вида. Общее сопротивление контура (R ij = R ji ) представляет собой алгебраическую сумму сопротивлений потребителей ветви (нескольких ветвей), одновременно принадлежащих i -ому и j -ому контурам. В эту сумму сопротивление входит со знаком «+», если контурные токи протекают через данное сопротивление в одном направлении (согласно), и знак «–», если они протекают встречно. Собственное сопротивление контура (R ii ) представляет собой арифметическую сумму сопротивлений всех потребителей, находящихся в i -ом контуре. Контурные ЭДС представляют собой алгебраическую сумму ЭДС источников, входящих в контур. Со знаком «+» в эту сумму входят ЭДС источников, действующих согласно с обходом контура, со знаком «–» входят ЭДС источников, действующих встречно. 4. Разрешить полученную систему уравнений относительно контурных токов, используя метод Крамера.
5. Определить токи ветвей через контурные токи по I закону Кирхгофа. 6. Проверить правильность расчетов при помощи баланса мощности. Если в цепи содержится q источников тока, количество совместно рассматриваемых уравнений сокращается на q и становится равным р – q, поскольку токи в таких ветвях известны Необходимо, чтобы каждый источник тока входил только в один контур. Метод узловых потенциалов. В том случае, когда п- 1 < p (n – количество узлов, p – количество независимых контуров), данный метод более экономичен, чем метод контурных токов. Выводится из первого закона Кирхгофа и обобщенному закону Ома(через потенциалы). 1. Обозначить все токи ветвей и их положительное направление. 2. Произвольно выбрать опорный узел (jn) и пронумеровать все остальные (n- 1) -e узлы. 3. Определить собственные и общие проводимости узлов, а также узловые токи, т.е. рассчитать коэффициенты в системе уравнений. Собственная проводимость узла (G ii ) представляет собой арифметическую сумму проводимостей всех ветвей, соединенных в i -ом узле. Общая проводимость i-ого и j-ого узлов (G ij = G ji ) представляет собой взятую со знаком «–» сумму проводимостей ветвей, присоединенных одновременно к i- ому и j- ому узлам. Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят! Узловой ток (J ii ) состоит из двух алгебраических сумм: первая содержит токи источников тока, содержащиеся в ветвях, соединенных в i -ом узле; вторая представляет собой произведение ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в i -ом узле. Со знаком «+» в эту сумму входят E и J источников, действие которых направлено к узлу, со знаком «–» остальные. 4. Записать систему уравнений в виде
В этой системе каждому узлу соответствует отдельное уравнение. 5. Полученную систему уравнений решить относительно неизвестных (n – 1) потенциалов при помощи метода Крамера. 6. С помощью обобщенного закона Ома рассчитать неизвестные токи. 7. Проверить правильность расчетов при помощи баланса мощности. Порядок расчета не зависит от вида источников, действующих в цепи. Однако, расчет упрощается в случае, когда между одной или несколькими парами узлов включены идеализированные источники ЭДС. Тогда напряжения между этими парами узлов становятся известными величинами, определенными условиями задачи. Для успешного решения подобных задач необходимо правильно обозначить опорный узел, в качестве которого может быть выбран только один из узлов, к которым присоединена ветвь с идеализированным источником ЭДС. Если таких ветвей q, то количество уравнений в системе сократится до k = n – 1 – q. Метод двух узлов Для разветвленной цепи, имеющей только два узла и произвольное количество ветвей, метод узловых потенциалов вырождается в метод двух узлов. Решение сводится к отысканию значения потенциала одного из узлов, т.к. потенциал другого узла может быть принятым равным нулю. Система уравнений превращается в одно уравнение:
при условии, что После определения U 12 токи ветвей и напряжения источников тока находят при помощи обобщенного закона Ома. Электрическая цепь и ее элементы. Реальная электрическая цепь - совокупность устройств, предназначенных для передачи, распределения и преобразования энергии. Содержит источники электрической энергии, приемники электрической энергии, измерительные приборы, коммутационную аппаратуру, соединительные линии и провода. Электрическая цепь представляет собойсовокупность связанных определенным образом источников, потребителей (или соответственно активных и пассивных элементов) и преобразователей электрической энергии. Цепь называют пассивной, если она состоит только из пассивных элементов, и активной, если в ней также содержатся активные элементы. Источником электрической энергии называют элемент электрической цепи, осуществляющий преобразование энергии неэлектрического вида в электрическую. Потребителем электрической энергии называют элемент электрической цепи, преобразующий электрическую энергию в неэлектрическую. Преобразователем электрической энергии называют устройство, изменяющее величину и форму электрической энергии. Для того чтобы выполнить расчет, необходимо каждое электротехническое устройство представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности идеализированных элементов(резистор, конденсатор, катушка индуктивности). Напряжение: Ток: Зависимость между током и напряжением на элементе цепи называется вольт-амперной характеристикой (ВАХ) элемента, которая обычно изображается графически. В качестве потребителя в теории электрических цепей постоянного тока выступает резистор, характеризующийся сопротивлением (R), для которого справедлив закон Ома:
Проводимость: Источники энергии моделируются с помощью источника ЭДС (Е), или источника напряжения, и источника тока (J). В большинстве случаев с увеличением тока напряжение источника уменьшается. Идеализированный источник напряжения – это элемент цепи, напряжение которого не зависит от тока и является заданной постоянной величиной. В действительности мы имеем дело с реальными источниками напряжения, которые отличаются от идеальных источников тем, что их напряжение с ростом потребляемого тока уменьшается. Любой реальный источник при сопротивлении нагрузки R >> R 0 может быть приведен к идеализированному следующим образом:
Идеализированный источник тока – это элемент цепи, ток которого не зависит от напряжения и является заданной постоянной величиной. У реального источника тока с ростом напряжения вырабатываемый ток уменьшается.Любой реальный источник тока может быть приведен к идеализированному следующим образом:
Обобщенный закон Ома.
Рассмотрим закон Ома для участка цепи, содержащего активные и пассивные элементы
Объединив эти две формулы, получаем:
Отсюда ток Аналогияно:
Объединив эти две формулы в одну, получим:
Обобщенный закон Ома для ветви, содержащей источник тока: Для содействующего источника тока
Для противодействующего источника тока
Объединенная форма обобщенного закона Ома для ветвей, содержащих источник тока:
где верхний знак соответствуют схеме, на которой U J и J сонаправлены.
|
||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


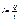
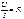
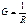 измеряется в Сименсах (См).
измеряется в Сименсах (См).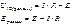
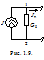
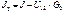 ,где J, G 0 – постоянные параметры.
,где J, G 0 – постоянные параметры.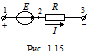
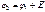
 .
.
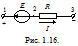

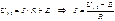 )
)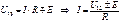 , - обобщенный закон Ома.
, - обобщенный закон Ома.

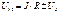 (1.25)
(1.25) (II З. К.) =>
(II З. К.) => 





 =>
=>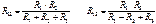 Аналогично
Аналогично 


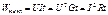 [Дж]
[Дж] [Вт]
[Вт]
 вместо
вместо  и
и  вместо
вместо 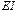 .
.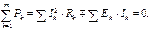
 .
. . Основан на II законе Кирхгофа
. Основан на II законе Кирхгофа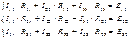


 (2.15)
(2.15)



