
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет неразветвленных электрических цепейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основой расчета одноконтурных (неразветвленных) электрических цепей, содержащих источники обоих видов и потребители, служат рассмотренные ранее законы Ома и Кирхгофа. Если в цепи нет источников тока, а параметры потребителей (R) и источников напряжения (Е) заданы, то задача обычно состоит в определении тока контура. Положительное направление искомого тока выбирается произвольно и составляется уравнение:
Если в цепи, кроме потребителе (R) и источников ЭДС (E), имеется источник тока (J), то задача обычно сводится к определению напряжения на источнике тока U J, т.к. ток контура I совпадает с заданным током источника J. Положительная полярность U Jвыбирается произвольно, но предпочтительно у острия стрелки ставить знак «+» (такой полярности соответствует формула:
Метод пропорциональных величин. В ветви наиболее удаленной от источника (R 6) задаются некоторым значением тока или напряжения. Для удобства расчетов обычно это 1А или 1В. Затем перемещаясь к началу цепи определяют поочередно токи и напряжения всех ветвей вплоть до ветви, содержащей источник. Тем самым определяют какие напряжение U вх и ток I в х . должен иметь источник для того, чтобы вызвать во всех ветвях токи и напряжения вычисленных значений. Если ЭДС (Е) или задающий ток (J) с этими значениями не совпадают, то необходимо пропорционально изменить вычисленные значения токов и напряжений ветвей путем умножениях их на отношение
Пусть I 6 = 1. Тогда I3 можно определить по I закону Кирхгофа: U 24 определяем по II закону Кирхгофа:
По закону Ома:
14) Метод эквивалентных преобразований. Формула токов в параллельных ветвях. Разветвленную цепь с одним источником обычно упрощают, преобразуя в неразветвленную.
Дальнейший расчет: Ток I3 определяется по закону Кирхгофа:
При расчетах удобно пользоваться формулой о токах в двух параллельных пассивных ветвях. Выведем ее на примере схемы. Напряжение
Тогда ток
Метод уравнений Кирхгофа. 1. Обозначить токи ветвей и произвольно выбрать их положительное направление. 2. Произвольно выбрать опорный узел и совокупность p = m – n + 1 независимых контуров. 3. Для всех узлов, кроме опорного, составить уравнения по I закону Кирхгофа. Таких уравнений должно быть (n – 1). 4. Для каждого выбранного контура составить уравнения по II закону Кирхгофа. Таких уравнений должно быть p. 5. Система m уравнений Кирхгофа с m неизвестными токами решается совместно и определяются численные значения токов. 6. Если необходимо, рассчитать с помощью обобщенного закона Ома напряжения ветвей или разность потенциалов узлов. 7. Проверить правильность расчета с помощью баланса мощности. Если в цепи есть q источников тока и контуры выбирать таким образом, чтобы каждый источник тока вошел только в один контур, то количество уравнений по II закону Кирхгофа можно уменьшить до m – n + 1 – q. Метод Контурных Токов За искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по II закону Кирхгофа, т.е. По найденным контурным токам при помощи I закона Кирхгофа определяются токи ветвей. Таким образом, методика расчета цепи постоянного тока методом контурных токов следующая: 1. Обозначить все токи ветвей и их положительное направление. 2. Произвольно выбрать совокупность p независимых контуров, нанести на схему положительное направление контурных токов, протекающих в выбранных контурах. 3. Определить собственные, общие сопротивления и контурные ЭДС и подставить их в систему уравнений вида. Общее сопротивление контура (R ij = R ji ) представляет собой алгебраическую сумму сопротивлений потребителей ветви (нескольких ветвей), одновременно принадлежащих i -ому и j -ому контурам. В эту сумму сопротивление входит со знаком «+», если контурные токи протекают через данное сопротивление в одном направлении (согласно), и знак «–», если они протекают встречно. Собственное сопротивление контура (R ii ) представляет собой арифметическую сумму сопротивлений всех потребителей, находящихся в i -ом контуре. Контурные ЭДС представляют собой алгебраическую сумму ЭДС источников, входящих в контур. Со знаком «+» в эту сумму входят ЭДС источников, действующих согласно с обходом контура, со знаком «–» входят ЭДС источников, действующих встречно. 4. Разрешить полученную систему уравнений относительно контурных токов, используя метод Крамера.
5. Определить токи ветвей через контурные токи по I закону Кирхгофа. 6. Проверить правильность расчетов при помощи баланса мощности. Если в цепи содержится q источников тока, количество совместно рассматриваемых уравнений сокращается на q и становится равным р – q, поскольку токи в таких ветвях известны Необходимо, чтобы каждый источник тока входил только в один контур. Метод узловых потенциалов. В том случае, когда п- 1 < p (n – количество узлов, p – количество независимых контуров), данный метод более экономичен, чем метод контурных токов. Выводится из первого закона Кирхгофа и обобщенному закону Ома(через потенциалы). 1. Обозначить все токи ветвей и их положительное направление. 2. Произвольно выбрать опорный узел (jn) и пронумеровать все остальные (n- 1) -e узлы. 3. Определить собственные и общие проводимости узлов, а также узловые токи, т.е. рассчитать коэффициенты в системе уравнений. Собственная проводимость узла (G ii ) представляет собой арифметическую сумму проводимостей всех ветвей, соединенных в i -ом узле. Общая проводимость i-ого и j-ого узлов (G ij = G ji ) представляет собой взятую со знаком «–» сумму проводимостей ветвей, присоединенных одновременно к i- ому и j- ому узлам. Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят! Узловой ток (J ii ) состоит из двух алгебраических сумм: первая содержит токи источников тока, содержащиеся в ветвях, соединенных в i -ом узле; вторая представляет собой произведение ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в i -ом узле. Со знаком «+» в эту сумму входят E и J источников, действие которых направлено к узлу, со знаком «–» остальные. 4. Записать систему уравнений в виде
В этой системе каждому узлу соответствует отдельное уравнение. 5. Полученную систему уравнений решить относительно неизвестных (n – 1) потенциалов при помощи метода Крамера. 6. С помощью обобщенного закона Ома рассчитать неизвестные токи. 7. Проверить правильность расчетов при помощи баланса мощности. Порядок расчета не зависит от вида источников, действующих в цепи. Однако, расчет упрощается в случае, когда между одной или несколькими парами узлов включены идеализированные источники ЭДС. Тогда напряжения между этими парами узлов становятся известными величинами, определенными условиями задачи. Для успешного решения подобных задач необходимо правильно обозначить опорный узел, в качестве которого может быть выбран только один из узлов, к которым присоединена ветвь с идеализированным источником ЭДС. Если таких ветвей q, то количество уравнений в системе сократится до k = n – 1 – q. Метод двух узлов Для разветвленной цепи, имеющей только два узла и произвольное количество ветвей, метод узловых потенциалов вырождается в метод двух узлов. Решение сводится к отысканию значения потенциала одного из узлов, т.к. потенциал другого узла может быть принятым равным нулю. Система уравнений превращается в одно уравнение:
при условии, что После определения U 12 токи ветвей и напряжения источников тока находят при помощи обобщенного закона Ома.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.149 (0.011 с.) |

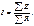
 ). Истинная полярность UJ совпадает с выбранной, если при расчете U Jвыражается положительным числом, и противоположна выбранной, если U J < 0. Искомое падение напряжения на источнике тока U J при отсутствии источников ЭДС определяется по формуле
). Истинная полярность UJ совпадает с выбранной, если при расчете U Jвыражается положительным числом, и противоположна выбранной, если U J < 0. Искомое падение напряжения на источнике тока U J при отсутствии источников ЭДС определяется по формуле  .
. или
или  .
.
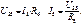


 , по I закону Кирхгофа:
, по I закону Кирхгофа:  .
.

 Если цепь питается источником тока, то определяется напряжение
Если цепь питается источником тока, то определяется напряжение 
 .
.

 по закону Ома определяется по формуле
по закону Ома определяется по формуле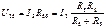
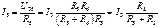
 . Основан на II законе Кирхгофа
. Основан на II законе Кирхгофа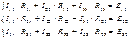


 (2.15)
(2.15)



