
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура электрической цепи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте К структурным или топологическим свойствам цепи относятся такие ее особенности, которые не связаны с характеристиками входящих в нее активных и пассивных элементов. К ним относятся следующие понятия: ветвь, узел, контур. Ветвью электрической цепи называют участок, элементы которого включены последовательно друг за другом и обтекаются одним и тем же током. Узлом электрической цепи называют место соединения нескольких ветвей. Узел связывает не менее трех ветвей и является точкой разветвления. Ветви считаются соединенными последовательно, если они обтекаются одним и тем же током. Ветви считаются соединенными параллельно, если они присоединены к одной и той же паре узлов. Контуром электрической цепи называется совокупность следующих друг за другом ветвей. Узлы, в которых эти ветви соединяются, являются точками разветвления. При обходе замкнутого контура начальная и конечная точки совпадают. Цепь, в которой отсутствуют разветвления, называют одноконтурной, при наличии разветвлений – многоконтурной. Многоконтурная цепь характеризуется числом независимых контуров. Совокупность независимых контуров определяется тем, что каждый из последующих контуров, начиная от элементарного, отличается по меньшей мере одной новой ветвью. Число независимых контуров может быть определено по формуле Эйлера:
Законы Кирхгофа. I закон Кирхгофа (для токов): алгебраическая сумма токов в узле равна нулю, или сумма притекающих и сумма истекающих токов одинаковы. Как правило, при суммировании притекающие токи берутся со знаком «+», а истекающие – со знаком «–». II закон Кирхгофа (для напряжений): алгебраическая сумма ЭДС всех источников, встречающихся при обходе контура, равна алгебраической сумме напряжений на всех потребителях. В алгебраической форме В сумму со знаком «+» входят ЭДС содействующих источников и со знаком «–» ЭДС противодействующих источников. При суммировании напряжений потребителей со знаком «+» берутся напряжения на всех потребителях, токи которых направлены согласно с обходом контура, и со знаком «–» берутся напряжения всех остальных потребителей. 8) Эквивалентные преобразования пассивных электрических цепей. Эквивалентное преобразование части пассивной электрической цепи состоит в такой ее замене другой пассивной цепью, при которой остаются неизменными токи и напряжения остальной цепи, не подвергшейся преобразованию. К простейшим преобразованиям относятся замена последовательно и параллельно соединенных потребителей эквивалентным потребителем. При последовательном соединении роль эквивалентного сопротивления играет сумма сопротивлений всех потребителей (рис. 1.11.).
При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
Это следует из I закона Кирхгофа:
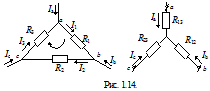
9-10) Эквивалентное преобразование «Звезда – треугольник»
В узлах a, b, c и треугольник, и звезда на рис. 1.14. соединяются с остальной частью схемы. Преобразование треугольника в звезду должно быть таковым, чтобы при одинаковых значениях потенциалов одноименных точек треугольника и звезды притекающие к этим точкам токи были одинаковы, тогда вся внешняя схема «не заметит» произведенной замены. Выразим U abтреугольника через параметры потребителей и притекающие к этим узлам токи. Запишем уравнения Кирхгофа для контура и узлов a и b.
Заменим в первом уравнении токи I 3 и I 2на соответствующие выражения:
Теперь получим выражение для этого же напряжения при соединении потребителей звездой:
Таким образом, сопротивление луча звезды равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений трех сторон треугольника. Формулы обратного преобразования можно вывести независимо, либо как следствие соотношений через проводимости:
или через сопротивления:
Баланс мощности. Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию:
По обобщенному закону Ома.
Выражения, записанные для ветви с источником напряжения, справедливы и для ветви с источником тока, если произвести подстановку Отсюда следует закон сохранения энергии, согласно которому алгебраическая сумма мощностей, подводимых ко всем ветвям разветвленной электрической цепи, равна нулю:
Существует еще одна форма записи баланса мощности:
В левой части суммируются мощности источников энергии, а в правой – мощности, преобразованные в потребителях в тепло. Мощности источников, отдающих энергию, берутся со знаком «+», а работающих в режиме потребителей – со знаком «–».
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 где m – количество ветвей, n – количество узлов, причем m > n всегда.
где m – количество ветвей, n – количество узлов, причем m > n всегда. (II З. К.) =>
(II З. К.) => 





 =>
=>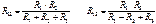 Аналогично
Аналогично 


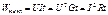 [Дж]
[Дж] [Вт]
[Вт]
 вместо
вместо  и
и  вместо
вместо 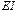 .
.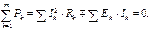
 .
.


