
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитный поток. Теорема Остроградского-Гаусса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Магнитный поток через поверхность S есть интеграл:
Тогда Очевидно, что:
Рассмотрим работу перемещения проводника с током в магнитном поле: На проводник с током будет действовать сила Ампера и проводник передвинется: Элементарная работа при перемещении проводника:
Вид сверху. Оказывается, что
1-а Тл это индукция такого однородного магнитного поля, которое создает максимальный вращательный момент Поле должно быть однородным. Если контур в неоднородном поле, то кроме вращательного момента возникает сила втягивающая рамку в область сильного поля.
Т.к. электрический ток, т.е. упорядоченное движение электрических зарядов, создает магнитное поле, то и обратно-переменное магнитное приводит к возникновению тока. Явление электромагнитной индукции по Фарадею: « В замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Этот ток называется индукционным». εi
Если рамка не закреплена,то она будет вращаться, и за dt Fa совершит работу dA: dA = IdФ. В рамке выделится тепло Джоуля-Ленца:
F=qVBsinα. Под действием силы Лоренца электроны будут двигаться вниз, аток направлен вверх: F=qE, qVB=qE, E=VB εi=U= −Δφ= −El= −BlV, E= Δφ /l, Δφ= El εi=U= −BlV
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.42.225 (0.011 с.) |

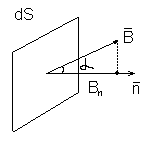 Магнитным потоком dФ (потоком вектора магнитной индукции) через площадку dS называется произведение площади этой площадки dS и проекции
Магнитным потоком dФ (потоком вектора магнитной индукции) через площадку dS называется произведение площади этой площадки dS и проекции  индукции B магнитного поля на направление внешней нормали n площадки dS.
индукции B магнитного поля на направление внешней нормали n площадки dS. ,
, 
 . Если поле однородное
. Если поле однородное  =const., а поверхность плоская и магнитное поле перпендикулярное к поверхности, то:
=const., а поверхность плоская и магнитное поле перпендикулярное к поверхности, то:  , [ Ф ]= Вебер (Вб). Магнитный поток через пов-сть равен одному веберу, если площадь поверхности равна одному квадратному метру, магнитное поле с индукцией 1 Тл перпендикулярно поверхности. 1 Вб = 1Тл × 1 м
, [ Ф ]= Вебер (Вб). Магнитный поток через пов-сть равен одному веберу, если площадь поверхности равна одному квадратному метру, магнитное поле с индукцией 1 Тл перпендикулярно поверхности. 1 Вб = 1Тл × 1 м  . Магнитный поток через поверхность численно равен числу магнитных силовых линий проходящих через эту поверхность или пропорционален числу магнитных силовых линий.
. Магнитный поток через поверхность численно равен числу магнитных силовых линий проходящих через эту поверхность или пропорционален числу магнитных силовых линий.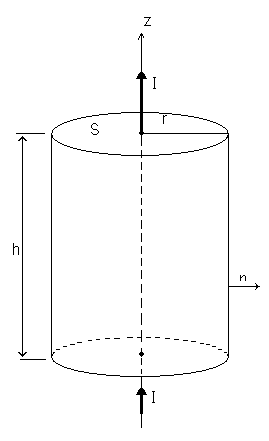 Теорема Остроградского - Гаусса: магнитный поток через любую замкнутую поверхность равна нулю, т.е:
Теорема Остроградского - Гаусса: магнитный поток через любую замкнутую поверхность равна нулю, т.е: 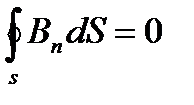 ,
,  . Теорема Остр – Г означает замкнутость магнитных силовых линий, т.е. отсутствие магнитных зарядов, на которых могли бы начинаться и кончаться магнитные силовые линии. Рассмотрим доказательство теоремы Остроградского – Гаусса для магнитного поля на примере бесконечного прямолинейного проводника с током I. В качестве поверхности S возьмем круговой цилиндр, с осью совпадающей с током. Магнитные силовые линии такого тока есть концентрические окружности с центром на оси тока.
. Теорема Остр – Г означает замкнутость магнитных силовых линий, т.е. отсутствие магнитных зарядов, на которых могли бы начинаться и кончаться магнитные силовые линии. Рассмотрим доказательство теоремы Остроградского – Гаусса для магнитного поля на примере бесконечного прямолинейного проводника с током I. В качестве поверхности S возьмем круговой цилиндр, с осью совпадающей с током. Магнитные силовые линии такого тока есть концентрические окружности с центром на оси тока. =0 (проекция на направление внешней нормали).
=0 (проекция на направление внешней нормали).
 31. Контур и виток с током в магнитном поле.
31. Контур и виток с током в магнитном поле.
 ,
, 
 Конечная работа это:
Конечная работа это:  ,
, 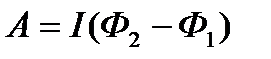
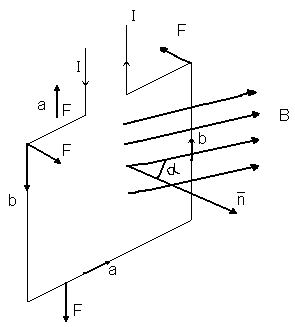
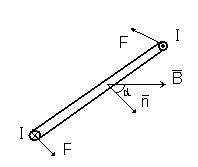 Рассмотрим прямоугольную рамку с током I в однородном магнитном поле
Рассмотрим прямоугольную рамку с током I в однородном магнитном поле  . Покажем, что в общем случае рамка будет вращаться. Это вид сбоку. Раз течет ток, то возникает сила Ампера:
. Покажем, что в общем случае рамка будет вращаться. Это вид сбоку. Раз течет ток, то возникает сила Ампера: 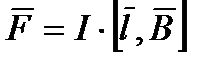 Сила Ампера будет действовать на ребра a перпендикулярные к ним и к магнитной индукции и будет только растягивать рамку.
Сила Ампера будет действовать на ребра a перпендикулярные к ним и к магнитной индукции и будет только растягивать рамку. -
- 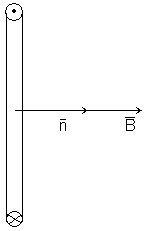 Магнитное поле создаваемое самой рамкой будет совпадать с индукцией
Магнитное поле создаваемое самой рамкой будет совпадать с индукцией  . Если контур повернется под действием сил на угол
. Если контур повернется под действием сил на угол 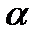 , то будет совершена работа этими силами.
, то будет совершена работа этими силами. ,
,  ,
,  . С другой стороны, так как магнитный поток через плоскую поверхность ограничи-вается рамкой, магнитный поток есть:
. С другой стороны, так как магнитный поток через плоскую поверхность ограничи-вается рамкой, магнитный поток есть:  , где S- площадь поверхности ограниченной рамкой.
, где S- площадь поверхности ограниченной рамкой.  , получ:
, получ: 
 ,
, 
 получим макс момент:
получим макс момент:  - определение магнитной индукции. 1Тл =
- определение магнитной индукции. 1Тл = 

 на рамку с током в 1 ампер и площадью поверхности
на рамку с током в 1 ампер и площадью поверхности  .
. 32. Явление электромагнитной индукции. Правило Ленца.
32. Явление электромагнитной индукции. Правило Ленца. Получим закон электромагнитной индукции, как следствие закона сохранения энергии:
Получим закон электромагнитной индукции, как следствие закона сохранения энергии: . По закону сохра-нения энергии: сумма dA и dQ равна работа источника тока. εIdt= IdФ+ I2 Rdt, εdt=dФ=IRdt, εi = −NdФ/dt
. По закону сохра-нения энергии: сумма dA и dQ равна работа источника тока. εIdt= IdФ+ I2 Rdt, εdt=dФ=IRdt, εi = −NdФ/dt 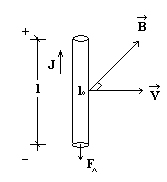 I=(ε− dФ/dt)/R, − dФ/dt= εi, I= (ε+ εi)/R. При помещении массивных проводников в переменное магнитное поле, в них возникают вихревые токи. Получим теперь явление электромагнитной индукции, как следствие действия силы Лоренца на проводники, движущиеся в магнитном поле. Пусть участок проводника помещен в магнитное поле с индукц. В и проводник перпендикулярен индукц. В. Пусть проводник движется со скоростью V.
I=(ε− dФ/dt)/R, − dФ/dt= εi, I= (ε+ εi)/R. При помещении массивных проводников в переменное магнитное поле, в них возникают вихревые токи. Получим теперь явление электромагнитной индукции, как следствие действия силы Лоренца на проводники, движущиеся в магнитном поле. Пусть участок проводника помещен в магнитное поле с индукц. В и проводник перпендикулярен индукц. В. Пусть проводник движется со скоростью V.


