
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле и его характеристики.Содержание книги
Поиск на нашем сайте Магнитное поле и его характеристики. В пространстве, окружающем электрические токи, существует поле, получившее название магнитное поле. Cвое название это поле получило в связи с тем, что оно оказывает ориентирующее воздействие на магнитную стрелку. наличие магнитного поля можно также обнаружить по его силовому воздействию на проводники с током и постоянные магниты. для изучения характеристик магнитного поля используют рамку с током. Рамка устанавливается в магнитном поле определенным образом. Для определения её положения вводят понятие положения нормали к рамке. Её направление определяют по правилу правого винта: Положительная нормаль к плоскости рамки направлена в сторону поступательного движения острия правого винта, головка которого вращается по направлению тока в рамке. За направление магнитного поля в конкретной точке пространства принимают направление, вдоль которого устанавливается положительная нормаль к рамке. Магнитным моментом контура с током называют векторную величину:
Если рамку с током установить с магнитном поле, то со стороны поля на рамку будет действовать вращающий момент. Индукция магнитного поля:
В скалярной форме:
Магнитное поле можно изобразить графически. Это делают с помощью линий магнитной индукции. Линии магнитной индукции проводят так, чтобы касательные к ним в каждой точке совпадали с направлением вектора Линии магнитной индукции поля, создаваемого прямым проводником с током, имеют вид концентрических окружностей. Линии магнитной индукции всегда замкнуты в отличие от линий напряженности электростатического поля. Поле имеющее замкнутые силовые линии называют вихревым, следовательно, магнитное поле – вихревое. В любом теле существуют микротоки, обусловленные движением электронов в атомах. Эти микротоки также создают магнитные поля. чтобы охарактеризовать внешнее магнитное поле, т.е. поле, создаваемое микротоками, вводят величину – напряженность магнитного поля.
Закон Био-Савара-Лапласа и его применение к расчету магнитного поля прямого тока. Этот закон позволяет рассчитать индукцию магнитного поля, создаваемого бесконечно малым элементом
В скалярной форме:
Направление вектора Для магнитного поля справедлив принцип суперпозиции: индукция результирующего магнитного поля, создаваемого несколькими токами или движущимися зарядами в какой-либо точке пространства, равна векторной сумме индукций магнитных полей, создаваемых в этой точке каждой из них в отдельности. В соответствии с законом Био-Савара-Лапласа:
В прямоугольном
Подставим это выражение в формулу
Если проводник бесконечно длинный, то:
В этом случае формула примет вид
Пример определения углов
Закон Ампера Этот закон позволяет рассчитать силу, действующую на элемент dl проводника с током I находящегося в магнитном поле dB=I[dl*B] Направление силы Ампера можно найти по правилу левой руки: левую руку располагают там чтобы перпендикулярная к проводнику с током составляющая вектора магнитной индукции входила в ладонь,4 вытянутых пальца были направлены по направлению тока, тогда отогнутый под прямым углом большой палец покажет направление силы Ампера.
a-угол между векторами B и dl dl-вектор направление которого совпадает с направлением тока + + B Проводник с током в магнитном поле
-... B
Из Рисунка видно, что при перемещении проводника АС на бесконечно малое расстояние dx сила F совершит работу dA=Fdx=IBLdx=IBds=IdФ где dS=Ldx-площадь прямоуг. ACC’A Работа по перемещению проводника с током в магнитном поле равна произведению силы тока магнитный поток, пересеченный движущимся проводником. В интегральной форме A=I Ф Работа по перемещению контура с током в магнитном поле Можно рассчитать по формуле A=I Ф =I(Ф2 –Ф1) где Ф изменение магн. потока, сцепленного с контуром Ф2, Ф1 - магн. Поток сцепленный с контуром в его конечном и начальном положении 8 Сила Лоренца - силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца Силу Лоренца можно найти с помощью закона Ампера. Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен: Подставляя в эту формулу выражение (2) для силы тока, получаем:
где
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Под действием силы Лоренца меняется лишь направление скорости частицы. Траектория движения заряженной частицы в однородном магнитном поле зависит от угла α между скоростью частицы и вектором магнитной индукции. Заряженная частица, влетающая в однородное магнитное поле параллельно линиям магнитной индукции, движется вдоль этих линий. В этом случае α = 0 и соответственно Fл = 0 . В однородном магнитном поле частица, движущаяся перпендикулярно линиям индукции магнитного поля, под действием силы Лоренца приобретает центростремительное ускорение: При движении заряженной частицы в однородном электрическом поле радиус движения частицы остается неизменным: Если угол
Закон Фарадея Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции
Знак минус показывает что увеличение потока ( Правило Ленца - правило для определения направления индукционного тока: индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток
11. Вращение рамки в магнитном поле. Явление электромагнитной индукции используют для преобразования энергии поля в энергию тока. Соответствующие устройства называют генераторами тока. Рассмотрим принципы действия такого генератора на примере рамки вращающейся в магнитном поле.
Будет изменятся и магнитный поток через рамку
В рамке возникает ЭДС индукции, изменяющееся с течением времени по гармоническому закону:
Где:
Переменное напряжение занимают и вращающиеся витки. С помощью щеток процесс преобразования магнитной энергии в электрическую обратим. Если по рамке, помещенной в магнитное поле, пропускать электрический ток, то на рамку будет действовать вращающий момент, и рамка начнет вращаться. На этом принципе основана работа электродвигателей, предназначенных для преобразования электрической энергии в механическую.
Ток при замыкании цепи. При замыкании цепи возникает внешняя ЭДС и ЭДС самоиндукции Вводим новую переменную u=IR- ε,получаем уравнение вида В момент замыкания(t=0) сила тока I=0 u=
, ТОК ПРИ РАЗМЫКАНИИ ЦЕПИ Цепь содержит источник тока с ЭДС, резистор с сопротивлением R и катушку индукции L. Отключим ток. Он в катушке начнет уменьшаться. Что приведет к возникновению εs = -L* (dI/dt) По закону Ома I= εs *R IR = -L *(dI/dt) dI/I = (-R/L)*dt интегрируем
I = I0* Таким образом сила тока убывает по кривой
Энергия магнитного поля Рассмотрим контур с L и I. С данным контуром сцеплен Ф= L*I Чтобы изменить Ф на dФ надо совершить А(работу). dA= I*d Ф= L*I*dI тогда А= следовательно, W= Рассмотрим магнитное поле внутри длинного соленоида W= Так как I = B l(эль)/ W= W= W/V= w- Объемная плотность Диа- и парамагнетизм. Все вещ-ва состоят из элемента круговых токов. По сути это атомы с вращающимися вокруг ядер электронами. Движение электронов в атоме имеет сложный характер. Оно состоит из 2-х вращательных процессов: Вращение вокруг ядра. (Этому движ-ю соответствует орбитальный маг. момент) Вращение вокруг собственной оси. (Этому движ-ю соответствует собственный маг. момент) Совокупность этих движений назыв-ся прецессией с нутацией. Исходя из данных движений, можно разделить диа- и парамагнетики. Под действием внешнего маг. поля у атома появляется составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов складываются и образуют собственное магнитное поле вещ-ва, ослабляющее внешнее маг. поле. Это называется диамагнитным эффектом. Диамагнетики – вещ-ва, намагничивающиеся во внешнем магнитном поле против направления поля. При отсутствии внешнего маг. поля магнитные моменты атомов равны нулю, т.к. у электронов атома орбитальные и собственные маг. моменты взаимно скомпенсированы. Парамагнетики – вещ-ва, намагничивающиеся во внешнем магнитном поле по направлению поля. При отсутствии внешнего маг. поля у их атомов магнитные моменты не равны нулю, т.к. орбитальные и собственные моменты его электронов не скомпенсированы. Но вследствие теплового движ-я молекул их магн. моменты ориентированы беспорядочно, поэтому парамагнетики магнитными св-ми не обладают. При внесении во внешнее маг. поле устанавливается преимущественная ориентация магнитных моментов атомов по полю. Т.о. парамагнетик намагничивается, создавая собственное маг. поле, совпадающее по направлению с внешним полем и усиливающее его. Это назыв-ся парамагнитным эффектом. Природа ферромагнетизма. Рассматривая магнитные св-ва ферромагнетиков, мы не высказывали физическую природу этого явления. Описательная теория ферромагнетизма была разработана французским физиком П. Вейссом. Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намагниченностью независимо от наличии внешнего намагничивающего поля. Спонтанное намагничение, однако, находится в кажущемся противоречии с тем, что многие ферромагнетики материалы даже при температурах ниже точки Кюри не намагничены. Для устранения этого противоречия Вейс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбивается на большое число малых макроскопических областей- доменов, самопроизвольно намагниченных до насыщения. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга, поэтому результирующий момент ферромагнетика равен нулю. Внешнее магнитное поле ориентирует по полю магнитные моменты всех доменов и ферромагнетик становится намагниченным. Ферромагнитными св-ми могут обладать только кристаллические вещества, в атомах которых имеются недостроенные внутренние электронные оболочки с некомпенсированными спинами. Так как ферромагнетизм наблюдается только в кристаллах, а они обладают анизотропией, то в монокристаллах ферромагнетиков должна иметь место анизотропия магнитных св-в. Действительно опыт показывает, что в одних направлениях в кристалле его намагниченность при данном значении напряженности магнитного поля наибольшая, в других – наименьшая. Существуют вещества в которых обменные силы вызывают антипараллельную ориентацию спиновых магнитных моментов электронов. Такие тела называются антиферромагнетиками. Для них также существует антиферромагнитная точка Кюри(т. Нееля), при которой магнитное упорядочение спиновых магнитных моментов нарушается и антиферромагнетик превращается в парамагнетик. В последнее время большое значение приобрели ферромагнетики – ферриты. Ферриты применяются для изготовления постоянных магнитов, ферритных антен, сердечников радиочастотных контуров, элементах оперативной памятив вычислительной технике и т.д. Магнитное поле и его характеристики. В пространстве, окружающем электрические токи, существует поле, получившее название магнитное поле. Cвое название это поле получило в связи с тем, что оно оказывает ориентирующее воздействие на магнитную стрелку. наличие магнитного поля можно также обнаружить по его силовому воздействию на проводники с током и постоянные магниты. для изучения характеристик магнитного поля используют рамку с током. Рамка устанавливается в магнитном поле определенным образом. Для определения её положения вводят понятие положения нормали к рамке. Её направление определяют по правилу правого винта: Положительная нормаль к плоскости рамки направлена в сторону поступательного движения острия правого винта, головка которого вращается по направлению тока в рамке. За направление магнитного поля в конкретной точке пространства принимают направление, вдоль которого устанавливается положительная нормаль к рамке. Магнитным моментом контура с током называют векторную величину:
Если рамку с током установить с магнитном поле, то со стороны поля на рамку будет действовать вращающий момент. Индукция магнитного поля:
В скалярной форме:
Магнитное поле можно изобразить графически. Это делают с помощью линий магнитной индукции. Линии магнитной индукции проводят так, чтобы касательные к ним в каждой точке совпадали с направлением вектора Линии магнитной индукции поля, создаваемого прямым проводником с током, имеют вид концентрических окружностей. Линии магнитной индукции всегда замкнуты в отличие от линий напряженности электростатического поля. Поле имеющее замкнутые силовые линии называют вихревым, следовательно, магнитное поле – вихревое. В любом теле существуют микротоки, обусловленные движением электронов в атомах. Эти микротоки также создают магнитные поля. чтобы охарактеризовать внешнее магнитное поле, т.е. поле, создаваемое микротоками, вводят величину – напряженность магнитного поля.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.013 с.) |




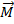 – вращающий момент, действующий на рамку с током.
– вращающий момент, действующий на рамку с током.
 – угол между
– угол между  и
и  .
.
 – магнитная постоянная;
– магнитная постоянная;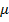 – относительная магнитная проницаемость среды.
– относительная магнитная проницаемость среды. ,
, 
 проводника, по которому проходит ток
проводника, по которому проходит ток 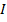 :
:
 – радиус-вектор, проведенный от элемента
– радиус-вектор, проведенный от элемента 
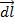 и
и  можно найти по правилу векторного произведения.
можно найти по правилу векторного произведения. :
:









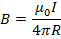
 и
и  .
. , к числу
, к числу  заряженных частиц, упорядоченно движущихся в этом участке проводника:
заряженных частиц, упорядоченно движущихся в этом участке проводника: 
 настолько малы, что вектор индукции магнитного поля
настолько малы, что вектор индукции магнитного поля  можно считать одинаковым в пределах этого отрезка проводника. Сила тока
можно считать одинаковым в пределах этого отрезка проводника. Сила тока  в проводнике связана с зарядом частиц
в проводнике связана с зарядом частиц  , концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения
, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения 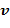 следующей формулой:
следующей формулой: 


 — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
— число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная: 
 где α — угол между вектором скорости и вектором магнитной индукции. Направление силы Лоренца определяется с помощью правила левой руки,
где α — угол между вектором скорости и вектором магнитной индукции. Направление силы Лоренца определяется с помощью правила левой руки,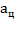 и движется по окружности.
и движется по окружности. между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции
между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
 ) вызывает ЭДС
) вызывает ЭДС 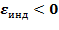 т.е поле индукционного тока направлено навстречу потоку; уменьшение потока (
т.е поле индукционного тока направлено навстречу потоку; уменьшение потока ( 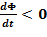 ) вызывает
) вызывает  т.е. направление потока и поля индукционного тока совпадают
т.е. направление потока и поля индукционного тока совпадают Если рамка вращается со скоростью ω, то угол α между векторами
Если рамка вращается со скоростью ω, то угол α между векторами  и
и  будет изменятся с течением времени:
будет изменятся с течением времени:

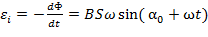 =
= 

 , препятствующая,согласно правилу Лнеца, возрастанию тока. По закону Ома, IR=ε+εs,или, IR=ε
, препятствующая,согласно правилу Лнеца, возрастанию тока. По закону Ома, IR=ε+εs,или, IR=ε  .
. ,где τ-время релаксации.
,где τ-время релаксации. ε, следовательно, интегрируя по u(от
ε, следовательно, интегрируя по u(от  ε до IR- ε) и t(от 0 до t), находим ln[(IR- ε)]/
ε до IR- ε) и t(от 0 до t), находим ln[(IR- ε)]/  ε=
ε=  τ или I=I0(1-e
τ или I=I0(1-e  ), где I0= ε/R- установившийся ток (при t→∞).
), где I0= ε/R- установившийся ток (при t→∞).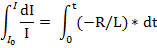
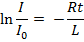
 , где
, где  = L/r – время релаксации
= L/r – время релаксации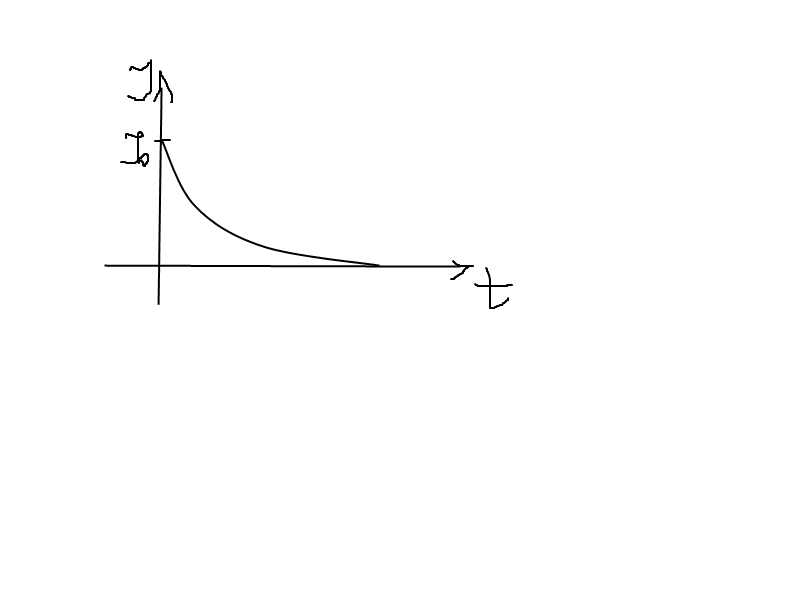



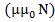 B =
B = 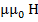 ,то
,то = (BH/2)*V, где Sl(эль)=V –объем соленоида
= (BH/2)*V, где Sl(эль)=V –объем соленоида



