
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитные поля соленоида и тороидаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Соленоид- цилиндрическая катушка, сост. Из большого количества витков, равномерно намотанных на общий сердечник. Если диаметр витков соленоида пренебрежимо мал по сравнению с его длиной, то такой соленоид называется бесконечно длинным. Магнитное поле бесконечно длинного соленоида является однородным, сосредоточенным внутри соленоида. Индукция магнитного поля внутри соленоида во всех точках одинакова.
Интеграл ABCDА рассмотрим на 4 участках, интегрируемых по AB, BC, CD, DА. AB и CD перпендикулярны линиям магнитной индукции, следовательно Тороид- кольцевая катушка, витки которой намотаны на сердечник, имеющий форму торо.
6) Магнитный поток. Теорема Гаусса для потока вектора
Потоком вектора магн. индукции через эту поверх-ть или магнитным потоком назыв. dФ = В скаляр. форме: dФ = B·cos где
Магнитный поток через произвольную поверх-ть равен:Ф = Если B = const и [Ф] = 1Вб (вебер) Рассмотрим маг. поток через бесконечно длинный соленоид, по кот. проходит ток где Магнитный поток через 1 виток соленоида равен: Через витки: Ѱ = полный магнитный поток (потокосцепление) Теорема Гаусса для потока вектора Поток вектора маг. индукции через любую замкнутую поверх-ть равен нулю.
Этот результат явл-ся следствием замкнутости линий магнитной индукции. Закон Ампера Этот закон позволяет рассчитать силу, действующую на элемент dl проводника с током I находящегося в магнитном поле dB=I[dl*B] Направление силы Ампера можно найти по правилу левой руки: левую руку располагают там чтобы перпендикулярная к проводнику с током составляющая вектора магнитной индукции входила в ладонь,4 вытянутых пальца были направлены по направлению тока, тогда отогнутый под прямым углом большой палец покажет направление силы Ампера.
a-угол между векторами B и dl dl-вектор направление которого совпадает с направлением тока + + B Проводник с током в магнитном поле
-... B
Из Рисунка видно, что при перемещении проводника АС на бесконечно малое расстояние dx сила F совершит работу dA=Fdx=IBLdx=IBds=IdФ где dS=Ldx-площадь прямоуг. ACC’A Работа по перемещению проводника с током в магнитном поле равна произведению силы тока магнитный поток, пересеченный движущимся проводником. В интегральной форме A=I Ф Работа по перемещению контура с током в магнитном поле Можно рассчитать по формуле A=I Ф =I(Ф2 –Ф1) где Ф изменение магн. потока, сцепленного с контуром Ф2, Ф1 - магн. Поток сцепленный с контуром в его конечном и начальном положении 8 Сила Лоренца - силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца Силу Лоренца можно найти с помощью закона Ампера. Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен: Подставляя в эту формулу выражение (2) для силы тока, получаем:
где
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Под действием силы Лоренца меняется лишь направление скорости частицы. Траектория движения заряженной частицы в однородном магнитном поле зависит от угла α между скоростью частицы и вектором магнитной индукции. Заряженная частица, влетающая в однородное магнитное поле параллельно линиям магнитной индукции, движется вдоль этих линий. В этом случае α = 0 и соответственно Fл = 0 . В однородном магнитном поле частица, движущаяся перпендикулярно линиям индукции магнитного поля, под действием силы Лоренца приобретает центростремительное ускорение: При движении заряженной частицы в однородном электрическом поле радиус движения частицы остается неизменным: Если угол
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.90.108 (0.008 с.) |

 Рассмотрим замкнутый контур ABCDохватывающий N витков
Рассмотрим замкнутый контур ABCDохватывающий N витков
 =0. BC вне соленоида, следовательно В=0.На участке DA
=0. BC вне соленоида, следовательно В=0.На участке DA  .
.  ,
,  -число витков на единицу длины соленоида.
-число витков на единицу длины соленоида. Тороид рассматривается как длинный соленоид, свитый в кольцо. Магнитное поле целиком сосредоточено внутри тороида.
Тороид рассматривается как длинный соленоид, свитый в кольцо. Магнитное поле целиком сосредоточено внутри тороида. . Длина тороида по его средней линии, пренебрегая небольшими различиями между внешним и внутренним окружностями кольца.
. Длина тороида по его средней линии, пренебрегая небольшими различиями между внешним и внутренним окружностями кольца.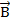 .
. Рассмотрим плоскую поверх-ть, имеющую бесконеч. малую площадь dS. Поверх-ть нах-ся в маг. поле.
Рассмотрим плоскую поверх-ть, имеющую бесконеч. малую площадь dS. Поверх-ть нах-ся в маг. поле.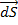 , где
, где 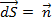 · dS
· dS · dS =
· dS =  · dS
· dS B·cos
B·cos  =
= 


 , формула принимает вид:Ф = BS
, формула принимает вид:Ф = BS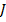 . Маг. индукция однородного поля внутри соленоида равна:B =
. Маг. индукция однородного поля внутри соленоида равна:B =  ,
,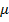 – относительная маг. проницаемость материала сердечника соленоида
– относительная маг. проницаемость материала сердечника соленоида = BS
= BS = N
= N 
 =
=  = 0
= 0 , к числу
, к числу  заряженных частиц, упорядоченно движущихся в этом участке проводника:
заряженных частиц, упорядоченно движущихся в этом участке проводника: 
 настолько малы, что вектор индукции магнитного поля
настолько малы, что вектор индукции магнитного поля  можно считать одинаковым в пределах этого отрезка проводника. Сила тока
можно считать одинаковым в пределах этого отрезка проводника. Сила тока  в проводнике связана с зарядом частиц
в проводнике связана с зарядом частиц  , концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения
, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения 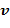 следующей формулой:
следующей формулой: 


 — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
— число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная: 
 где α — угол между вектором скорости и вектором магнитной индукции. Направление силы Лоренца определяется с помощью правила левой руки,
где α — угол между вектором скорости и вектором магнитной индукции. Направление силы Лоренца определяется с помощью правила левой руки,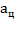 и движется по окружности.
и движется по окружности. между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции
между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции


