
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б12.Циркуляция вектора магнитной индукции ,магнитное поле соленоида.Содержание книги
Поиск на нашем сайте
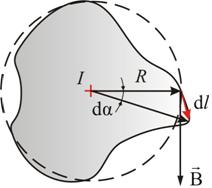
Возьмем контур l (рис. 2.8), охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции
Рис. 2.8 Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор
это теорема о циркуляции вектора
Рис. 2.9 Итак,
т.е. циркуляция вектора
Рис. 2. Итак, циркуляция вектора магнитной индукции Такие поля, называются вихревыми или соленоидальными Магнитному полю нельзя приписывать потенциал, как электрическому полю. Этот потенциал не был бы однозначным: после каждого обхода по контуру он получал бы приращение Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Опыт показывает, что линии
Рис. 2.1 Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричны относительно такой плоскости витки создают поле, в котором вектор перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида внутри и вне его.
Рис. 2.12Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным. Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.
Рис. 2.13
Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда
где Если отрезок 1–2 внутри соленоида, контур охватывает ток:
где n – число витков на единицу длины, I – ток в соленоиде (в проводнике). Тогда магнитная индукция внутри соленоида:
Вне соленоида:
Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри. Произведение nI – называется число ампер витков на метр. У конца полубесконечного соленоида, на его оси магнитная индукция равна:
Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца. Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем: · В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:
где L – длина соленоида, R – радиус витков. · В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле
Рис. 2.14 На рисунке 2.15 изображены силовые линии магнитного поля: а) металлического стержня; б) соленоида; в) железные опилки, рассыпанные на листе бумаги, помещенной над магнитом, стремятся вытянуться вдоль силовых линий; г) магнитные полюсы соленоида.
Рис. 2.15
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.188.152 (0.01 с.) |

 , т.е.
, т.е.  .
.
 где
где  – проекция d l на вектор
– проекция d l на вектор  , где R – расстояние от прямой тока I до d l.
, где R – расстояние от прямой тока I до d l. .Отсюда
.Отсюда
 , и следовательно
, и следовательно ,
,

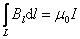 , где I – ток, охваченный контуром L. Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.Если контур охватывает несколько токов, то
, где I – ток, охваченный контуром L. Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.Если контур охватывает несколько токов, то ,
,
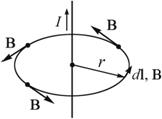
 позволяет легко рассчитать величину В от бесконечного проводника с током (рис. 2.10):
позволяет легко рассчитать величину В от бесконечного проводника с током (рис. 2.10):  .
.
 :
:  ).
). .
. Применим теорему о циркуляции вектора
Применим теорему о циркуляции вектора 
 для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).
для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).


 Второй и четвёртый интегралы равны нулю, т.к.вектор перпендикулярен направлению обхода, т.е
Второй и четвёртый интегралы равны нулю, т.к.вектор перпендикулярен направлению обхода, т.е  .
.
 – магнитная индукция на участке 1–2 – внутри соленоида,
– магнитная индукция на участке 1–2 – внутри соленоида,  – магнитная проницаемость вещества.
– магнитная проницаемость вещества.

 и
и  .
. ,
,
 ,
,
 ,
,






