
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Остроградского-Гаусса.Содержание книги
Поиск на нашем сайте
Определим поток напряжённости поля электрических зарядов через некоторую замкнутую поверхность, окружающую эти заряды. Рассмотрим сначала случай сферической поверхности радиуса R, окружающей один заряд, находящийся в ее центре
Таким образом, полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности, поделенной на ee0. Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.
Б4.Работа сил электрического поля при перемещении зарядов. Циркуляция вектора напряжённости.) Работа электростатического поля потенциального поля Пусть в поле заряда q перемещает заряд q’ из положения 1в 2,тогда поле будет совершена работа
Тогда работа: Что работа не зависит от пути перемещения,а определяется начальным и конечным положением заряда q’,следовательно силы электростатического поля яв-ся потенциальными. Их работа по замкнутому контуру будут=0 F –проекция вектора напряж. на направления контура. Послед.выражение наз-ся циркуляцией вектора E по замкнутому контуру и оно =0.Использую только в электростатич. Поле.
Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда где -
Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L
Так как d/cosa=d r, то
Работа при перемещении заряда Q 0 из точки 1 в точку 2
Из формулы (83.1) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
Формула (83.3) справедлива только для электростатического поля. В дальнейшем будет показано, что для поля движущихся зарядов условие (83.3) не выполняется (для него циркуляция вектора напряженности отлична от нуля). Б5.Потенциал электрического поля. Потенциал поля точечного заряда, системы зарядов. как видно из ур-я работы и учтя,что электростатическое поле яв-ся потенцильным, мы знаем,что тела помещенные в такие поля обладают энергией,поэтому выражение для работы мы можем записать,как убыль потенц.энергии.
Потенциал. Энергия будет равна.Первоначальный рисунок помещает заряд q’,тогда потен. Энергия будет равна,помещаем q2’
Посмотрим на правую часть,в неё входят величины которые характер.электрич. поле. Потенциал,это есть потенциал. Энергия данного заряда,помещенный в данную точку или.потенциал-это калярная величина. Если поле создается системой зарядов,то потенциал результирующий в любой точке пространства будет равен алгебраической сумме потенциалов,которое создается каждым зарядом в этой точке отдельно.потенциал-это энергетическая характеристика энергостатического поля.Потенциал энергии будет равен Потенциал электрического поля. Потенциал поля точечного заряда, системы зарядов.Внося в данную точку поля различные пробные заряды
Б6.Связь между напряжённостью и потенциалом. напряженность E.Потенциал пропорционален между ними должна быть связь аналогичная связи между силой и энергией.связь.Работа с одной стороны может быть записана;с другой стороны как (убыль потен.энергии) Тогда за L взяли произв. Направления.
Grad скаляр. Величины это есть вектор,он направлен в сторону наибыстрейшего возрастания этой функции, следовательно,что E напряж.направлен против grad потенциала. электрическое поле характеризуется двумя физическими величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика). Выясним как они связаны между собой. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал Из выражения (84.4) следует, что единица потенциала — вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная в § 79 единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Н×м/(Кл×м)=1 Дж/(Кл×м)=1 В/м. Из формул (84.3) и (84.4) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.20.66 (0.008 с.) |

 Напряженность поля по всей сфере одинакова и равна
Напряженность поля по всей сфере одинакова и равна иловые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы Sn, следовательно
иловые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы Sn, следовательно  т.к
т.к 
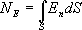
 Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула (13.6) справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е.
Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула (13.6) справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е.  или
или 
 из одной точки электростатического поля в другую на отрезке пути
из одной точки электростатического поля в другую на отрезке пути  , по определению равна
, по определению равна 
 угол между вектором силы F и направлением движения
угол между вектором силы F и направлением движения 
 Как видно из рисунка
Как видно из рисунка  тогда получим
тогда получим 

 Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.
Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю. Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории (рис. 132) перемещается другой точечный заряд Q 0, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении d l равна
Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории (рис. 132) перемещается другой точечный заряд Q 0, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении d l равна

 не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными
 Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути d l равна Е d l = El dl, где El = E cos a — проекция вектора Е на направление элементарного перемещения. Тогда формулу (83.2) можно записать в виде
Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути d l равна Е d l = El dl, где El = E cos a — проекция вектора Е на направление элементарного перемещения. Тогда формулу (83.2) можно записать в виде Интеграл
Интеграл  называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (83.3), называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.
называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (83.3), называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность. мы будем, соответственно, изменять потенциальную энергию, т.е. получим различные
мы будем, соответственно, изменять потенциальную энергию, т.е. получим различные  . Но отношение потенциальной энергии к заряду остается величиной постоянной. Следовательно для характеристики поля можем использовать это отношение. Обычно оно обозначается буквой
. Но отношение потенциальной энергии к заряду остается величиной постоянной. Следовательно для характеристики поля можем использовать это отношение. Обычно оно обозначается буквой  и называется потенциалом поля в данной точке
и называется потенциалом поля в данной точке  Потенциал является энергетической характеристикой поля. Он численно равен работе, которую надо затратить против сил электрического поля при перенесении единичного положительного точечного заряда из бесконечности в данную точку поля. Единица измерения потенциала - вольт. С учетом (1.16)
Потенциал является энергетической характеристикой поля. Он численно равен работе, которую надо затратить против сил электрического поля при перенесении единичного положительного точечного заряда из бесконечности в данную точку поля. Единица измерения потенциала - вольт. С учетом (1.16)  Когда поле образовано несколькими произвольно расположенными зарядами
Когда поле образовано несколькими произвольно расположенными зарядами  , создаваемых каждым зарядом в отдельности, т.е.
, создаваемых каждым зарядом в отдельности, т.е.  Если из точки “а” в точку “b” электрического поля перемещается заряд q’, то при этом совершается работа против электрических сил, равная
Если из точки “а” в точку “b” электрического поля перемещается заряд q’, то при этом совершается работа против электрических сил, равная  где
где  и
и 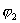 - потенциалы поля в точках “а” и ” b”.Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
- потенциалы поля в точках “а” и ” b”.Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом: 


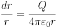 В СИ за единицу разности потенциалов принимают Вольт (В), Разность потенциалов между двумя точками поля равна одному Вольту, если для перемещения между ними заряда в один Кулон нужно совершить работу в один Джоуль
В СИ за единицу разности потенциалов принимают Вольт (В), Разность потенциалов между двумя точками поля равна одному Вольту, если для перемещения между ними заряда в один Кулон нужно совершить работу в один Джоуль 
 , на близко расположенную эквипотенциальную поверхность, имеющую потенциал
, на близко расположенную эквипотенциальную поверхность, имеющую потенциал 
 Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения
Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения  С другой стороны
С другой стороны  Из этих уравнений получаем
Из этих уравнений получаем  знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала. потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.
знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала. потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.



