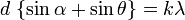Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б23. Распространение волн в упругой среде. Уравнения плоской и сферической волн. Уравнение плоской волны, Распространение в произвольном направлении.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде с некоторой скоростью v. Процесс распространения колебаний называется волной. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебания частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн. В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.
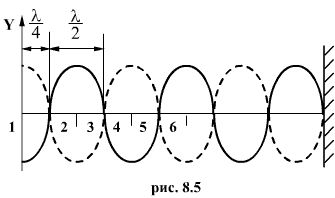
На рис.8.1 показано движение частиц при распространении в среде поперечной волны. Номерами 1,2,3 и т.д. обозначены частицы, отстоящие друг от друга на расстоянии, равном В момент времени равный периоду (t = Т), точки 1 и 5, находящиеся в положении равновесия, имеют одинаковое смещение и одинаковое направление движения (вверх). Поэтому говорят, что точки I и 5 имеют одинаковые фазы. В отличие от этого точки 1 и 3, хотя смещения у них одинаковы, движутся в противоположные стороны, поэтому говорят, что точки 1 и 3 находятся в противоположных фазах. Расстояния между точками 1 и 5 определяет длину волны λ т.е. длиной волны λ называется, расстояние между ближайшими точками волны, колеблющимися в одинаковых фазах. Периодом волны Т называют время одного полного колебания ее точек. Величина, обратная периоду, называется частотой волны. Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой:
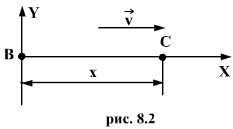
Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле: где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных. Составим уравнение, которое позволит находить смещение всякой точки волны в любой момент времени. Пусть в точке В рис.8.2 находится источник колебаний. Волны со скоростью v распространяются от источника колебаний вдоль прямой.
Уравнение колебаний точки В задано в виде: Все точки вправо от В, например точка С, повторяют колебания точки В с некоторым запозданием. Напишем уравнение колебаний точки С. Если точка В колеблется в течении времени t, то колебания дойдут до точки С по истечении времени
Расстояние от точки В до точки С, равное х, волна проходит со скоростью
где λ - длина волны Обозначим
которое называется уравнением плоской одномерной волны и определяет смещение любой точки среды, находящейся на расстоянии х от излучателя в данный момент. Величина
называется фазой волны. Получим уравнение плоской волны, распространяющейся в направлении, образующем с осями координат х, у, z углы α,β, γ Пусть колебания в плоскости, проходящей через начало координат, имеют вид
Возьмем волновую поверхность (плоскость), отстоящую от начала координат на расстоянии l. Колебания в этой плоскости будут отставать от колебаний в точке О (рис.8.3) на время
Выразим расстояние l через радиус-вектор
Отношение
Чтобы перейти от радиуса - вектора точки к ее координатам х, у, z, выразим скалярное произведение
где
Б24.Волновое уравнение для эпизодических колебаний. Вектор Пойтинга. оказалось,что ур-е волны яв-ся решением некоторого дифференциального ур-я 2-го порядка.найдем его.Для этого ур-е (4)продифференцируем дважды по каждой переменной.
Это есть символическое выражение вторых производных по x,y,z от функций этих переменных,тогда (6) из (1) выражения с учетом (7)-волновое ур-е для мех. Волн.Пусть ур-е (3) в комплексном виде может быть записано как аналогичное выражение (3)Если у нас имеется электромагнитная волна то,как известно в электромагн. колеблется 2 вектора вектор E и H
Тогда волновое ур-е для электромагнитной волны запишется
Ур-е волны Для любого момета времени плотность энергия равна сумме плотностей()E(электрич. Поле)+E(магнитного поля) Для любого момента времени плотность энергии равны (9),тогда равны последнее выражение,можем записать = (10)из(8)выражения с учетом (9) (10)может быть записано,как (12)тогда по скольку E иH –это вектора,то j=(EH),j-плотность потока.последнее выражение наз-ся вектор Пойнтинга Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
Продифференцируем дважды по каждой переменной уравнение (8.6):
Сложим последние три уравнения и получим
Из (8.7) следует
Это уравнение носит название волнового уравнения. Всякая функция, удовлетворяющая этому уравнению описывает некоторую волну. Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор S непрерывен на границе двух сред.
Б25.Интерференция волн, условия максимума и минимума. Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.[1]Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн. Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера. При интерференции энергия волн перераспределяется в пространстве.[1] Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн. При наложении некогерентных волн средняя величина квадрата амплитуды результирующей волны равна сумме квадратов амплитуд накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий ее колебаний, обусловленных всеми некогерентными волнами в отдельности. ) это есть процесс наложения волн(когерентных волн)в результате чего в одних точках пространства наблюдается усиление,а в других ослабление колебаний.Когерентные считаются волны у которых одна и та же частота и сохраняется постоянство разности фаз.Обычно из 1 источника с помощью зеркал Френеля получают когерентные источники.Пусть в точке О произошло образование 2-х когерентных волн,тогда в точке наблюдения P
Где v,v -фазовые скорости волн.c-скорость света.Тогда разность фаз
-оптическая длина хода. –оптическая разность хода волны. –длина волны в вакууме. –разность фаз. Т.е.колебания от когерентных источников придут в точку наблюдения в фазе,следовательно,условие (2)-это есть условие max при интерференции.Если
26Стоячие волны Частный случай интерференции волн,имеющих одну и ту же амплутуду.Пусть волна распространяется вдоль положит. Оси x в отрицат. при наложении получаем результирующую волну
Ур-е стоячей волны ампл.= амплитуда зависит от x.Если то амплитуда достигает max значения -эти точки наз-ся пучностями,тогда координата пучности n(принимает значения 1,2,3….),то в этом случае амплитуда=0.Эти точки наз-ся узлами пучности В этом случае расстояние между узлами,а так же между пучностями= Расстояние между пучностью и узлом.При переходе через узел фаза меняется на π,т.е. колебание частиц,находящихся по разным сторонам от узла находятся в противофазе. Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает приотражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения. Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну. Уравнение стоячей волны можно получить сложением уравнения падающей волны
и уравнения отраженной волны
Это уравнение стоячей волны определяет смещение любой точки волны.
не зависит от времени и определяет амплитуду любой точки с координатой х. Каждая точка совершает гармоническое колебание с периодом Т. Амплитуда Аст для каждой точки вполне определена. Но при переходе от одной точки волны к другой она изменяется в за
В стоячей волне все точки среды, в которой они распространяются, расположенные между двумя соседними узлами, колеблются в одной фазе. Точки среды, лежащие по разные стороны от узла, колеблются в противофазе -фазы их отличаются на π. т.е. при переходе через узел фаза колебаний скачкообразно меняется на π. В отличие от бегущих волн в стоячей волне отсутствует перенос энергии вследствие того, что образующие эту волну прямая и обратная волны переносят энергию в равных количествах и в прямом и в противоположном направлениях. В том случае, когда волна отражается от среды более плотной, чем та среда, где распространяется волна, в месте отражения возникает узел, фаза изменяется на противоположную. При этом говорят, что происходит потеря половины волны. Когда волна отражается от среды менее плотной в месте отражения, появляется кучность, и потери половины волны нет.
Б.27Дифракция волн. Зоны Фриэйлера. Дифракция Фриэйлера от простейших преград. Обусловлена рядом явлений наблюдаемых при распространении волн в среде с резкими неоднородными и связанные с отклонением от законов геометрической оптики.Частным случаем:огибание волн припятствия и заход колебаний в область геометрической теме.Явление дифракции может быть объяснено с помощью принципа Гюйгенса.Однако,определить результирующую амплитуду и интенсивность колебаний в любой точке пространства.Этот принцип был дополнен Френелем согласно,которому необходимо учитывать амплитуды и фазы вторичных волны.Любой элемент сферической волне яв-ся источником вторичных волн.Учет амплитуды и фазы вторичных волн позволяет определить результирующую амплитуду и интенсивность в любой точке пространства тогда -колебания которое придет в точку наблюдения от Тогда результирующим колебанием по всей поверхности (аналогичное выражение Гюйгенса-Френеля) k-это коэфициент,который угла между нормалью ds и нормалью r обращается в 0при Зоны Френеля Волновая поверхность разбиваем на кольцевые зоны т.о.,чтобы расстояние от краев зоны до точки наблюдения отличалась на,т.е. расстояние от края,тогда от аналогичных точек двух соседних зон колебания в точке наблюдения придут в противофазе,а следовательно и под двух соседних зон колебания в точке наблюдения придут в противозазу.для того чтобы определить амплитуду колебания необходимо определить s зон
Б.28Дифракция щелей. Дифракционная решётка. В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Математическое представление принципа Гюйгенсаиспользуется для написания исходного Рассмотрим монохроматическую плоскую волну с амплитудой Если разрез находится в плоскости x′-y′, с центром в начале координат, тогда может предполагаться, что дифракция производит волну ψ на расстоянии r, которая расходится радиально и вдалеке от разреза можно записать:
Расстояние r от щели определяется как:
Предполагая случай дифракции Фраунгофера, получим условие
Видно, что 1/ r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.
Здесь мы введём некую константу 'C', которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля. В случае дифракции Фраунгофера
Используя формулу Эйлера и её производную:
где ненормированная синкус функция определена как Подставляя
Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья. Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d. Если известно число штрихов ( Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:
где
Если же свет падает на решётку под углом
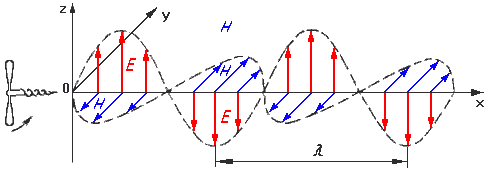
Б.29Поляризация электромагнитных волн. Направления электрического E и магнитного H полей в пространственной бегущей электромагнитной волне лежат в плоскости, перпендикулярной направлению движения волны. Направления полей соответствуют «правилу буравчика»: при повороте от вектора Е, расположенного вертикально (ось Z) к вектору H, лежащему в горизонтальной плоскости (ось Y) продвижение буравчика совпадает с направлением распространения волны (вдоль оси X)
На рис электрическая составляющая поля во все моменты остается в вертикальной плоскости. Пространственная ориентация этой составляющей служит признаком свойства волн, называемого поляризацией. Волна, показанная в данном примере, называется вертикально поляризованной. В зависимости от способа получения волн, поляризация может быть также горизонтальной или наклонной. Если в процессе распространения волн поляризация не изменяется, то она называется линейной.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.127.59 (0.011 с.) |


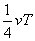 , т.е. на расстоянии, проходимом волной за четверть периода колебаний, совершаемых частицами. В начальный момент времени (t = 0) все точки расположены на прямой и ни одна из них не выходит из положения равновесия. Приведем точку 1 в гармоническое колебание с периодом Т, направленное перпендикулярно линии 1-5. Гак как частицы среды связаны между собой силами упругости, они тоже приходят в колебания, но с некоторым запаздыванием. Через четверть периода
, т.е. на расстоянии, проходимом волной за четверть периода колебаний, совершаемых частицами. В начальный момент времени (t = 0) все точки расположены на прямой и ни одна из них не выходит из положения равновесия. Приведем точку 1 в гармоническое колебание с периодом Т, направленное перпендикулярно линии 1-5. Гак как частицы среды связаны между собой силами упругости, они тоже приходят в колебания, но с некоторым запаздыванием. Через четверть периода  точка 1 отклонится от линии равновесия на максимальное смещение. Колебание начали все точки, лежащие слева от точки 2. По истечении времени
точка 1 отклонится от линии равновесия на максимальное смещение. Колебание начали все точки, лежащие слева от точки 2. По истечении времени 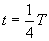 начнет подниматься вверх и точка 2. При
начнет подниматься вверх и точка 2. При  , первая точка вернется в положение равновесия, вторая точка достигнет максимального отклонения, и колебания дойдут до точки 3. При
, первая точка вернется в положение равновесия, вторая точка достигнет максимального отклонения, и колебания дойдут до точки 3. При 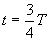 точка 1 достигнет максимального отрицательного смещения, точка 2 вернется в положение равновесия и колебания достигнут точки 4. Наконец, за время, равное периоду t = Т, точка 1 вернется в положение равновесия, совершив полностью одно колебание. Колебания распространились до точки 5, все колеблющиеся точки образуют волну. При дальнейших колебаниях точек волновой процесс распространится вправо от точки 5. В рассмотренном случае образования поперечной волны каждая частица движется только вверх и вниз. У наблюдателя же создается впечатление, что «волна бежит», хотя в действительности происходит только передача движения от одной точки среды к другой.
точка 1 достигнет максимального отрицательного смещения, точка 2 вернется в положение равновесия и колебания достигнут точки 4. Наконец, за время, равное периоду t = Т, точка 1 вернется в положение равновесия, совершив полностью одно колебание. Колебания распространились до точки 5, все колеблющиеся точки образуют волну. При дальнейших колебаниях точек волновой процесс распространится вправо от точки 5. В рассмотренном случае образования поперечной волны каждая частица движется только вверх и вниз. У наблюдателя же создается впечатление, что «волна бежит», хотя в действительности происходит только передача движения от одной точки среды к другой. Так как
Так как 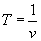 то,
то,
 , а поперечной:
, а поперечной: 
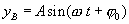
 , поэтому время колебаний точки С будет меньше t и составит
, поэтому время колебаний точки С будет меньше t и составит  . Тогда уравнение колебаний точки С запишется:
. Тогда уравнение колебаний точки С запишется: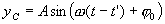
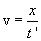 , откуда
, откуда 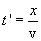 . С учетом
. С учетом 
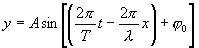
 эта величина называется волновым числом. Тогда получим следующее уравнение
эта величина называется волновым числом. Тогда получим следующее уравнение
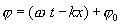
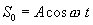 .
.
 тогда уравнение волны
тогда уравнение волны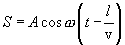
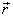 точек рассматриваемой поверхности. Для этого введем единичный вектор
точек рассматриваемой поверхности. Для этого введем единичный вектор  нормали к волновой поверхности. Скалярное произведение
нормали к волновой поверхности. Скалярное произведение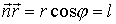
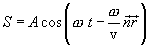
 равно волновому числу k. Вектор
равно волновому числу k. Вектор 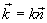 равный по модулю волновому числу
равный по модулю волновому числу 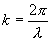 и имеющий направление вдоль нормали к волновой поверхности называется волновым вектором. Введя вектор
и имеющий направление вдоль нормали к волновой поверхности называется волновым вектором. Введя вектор  , получим
, получим
 через проекции векторов на координатные оси:
через проекции векторов на координатные оси:

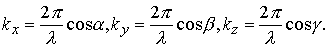
 где E и H — векторы напряжённости электрического и магнитного полей соответственно.
где E и H — векторы напряжённости электрического и магнитного полей соответственно.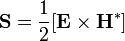 (в комплексной форме),где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор Sнепрерывен на границе двух сред.
(в комплексной форме),где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор Sнепрерывен на границе двух сред.
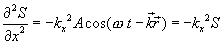


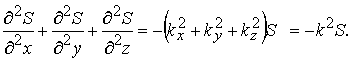
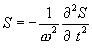
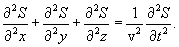


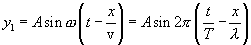
 Отраженная волна движется в направлении, противоположном падающей волне, поэтому расстояние х берем со знаком минус. Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме
Отраженная волна движется в направлении, противоположном падающей волне, поэтому расстояние х берем со знаком минус. Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме 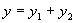 . После несложных преобразований, получаем
. После несложных преобразований, получаем
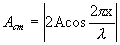
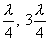 висимости от расстояния х. Если придавать х значения, равные и т.д., то при подстановке в уравнение (8.16) получим
висимости от расстояния х. Если придавать х значения, равные и т.д., то при подстановке в уравнение (8.16) получим 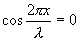 . Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно
. Следовательно, указанные точки волны остаются в покое, т.к. амплитуды их колебаний равны нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания происходят с максимальной амплитудой, называются пучностями. Расстояние между соседними узлами (или пучностями) называются длиной стоячей волны и равно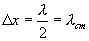 где λ - длина бегущей волны.
где λ - длина бегущей волны.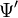 с длиной волны λ падающую на экран с щелью, ширина которой a.
с длиной волны λ падающую на экран с щелью, ширина которой a.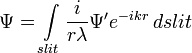 пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от
пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от  до
до  ), и бесконечна в y направлении ([
), и бесконечна в y направлении ([  ,
,  ]).
]).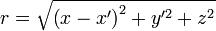
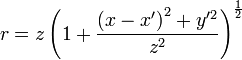
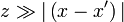 . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:
. Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде: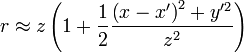
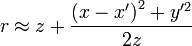




 мало, поэтому
мало, поэтому  . такое же приближение верно и для
. такое же приближение верно и для 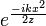 . Таким образом, считая
. Таким образом, считая 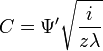 , приводит к выражению:
, приводит к выражению:

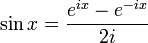 и
и 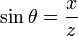 .
.
 .
. в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде
в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде  волны в зависимости от угла θ:
волны в зависимости от угла θ: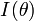
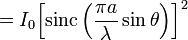
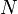 ), приходящихся на 1 мм решётки, то период решётки находят по формуле:
), приходящихся на 1 мм решётки, то период решётки находят по формуле:  мм.
мм.
 — период решётки,
— период решётки,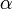 — угол максимума данного цвета,
— угол максимума данного цвета, — порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,
— порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки, — длина волны.
— длина волны. , то:
, то: