
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б2. Электрическое поле. Напряжённость поля. Принцип суперпозиции полей. Силовые линии поля. Поле диполя.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электрическое поле — одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела. Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
Электрическое поле наглядно изображается с помощью силовых линий. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку 1м2, перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля. Электрическое поле называется однородным, если во всех его точках напряженность Е одинакова. В противном случае поле называется неоднородным.
При положительном заряде, образующем поле, вектор напряженности направлен вдоль радиуса от заряда, при отрицательном - вдоль радиуса по направлению к заряду. Исходя из положительного заряда (или входя в отрицательный заряд) силовые линии теоретически простираются до бесконечности.
. Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
Напряж.данной точки будет равна 1.Если 3,то 3. Договоримся,что из поожительных выходят,а в отрицательный заряд входят
Силовая линия.Выбрали площадку ds, n-нормаль,тогда потоком вектора e будет наз-ся величина -скалярное произведение. Имеется конечная площадка ds,тогда поток Если поверхность замкнутая,то поток через замкнутую поверхность Замкнт. Поверхность разделяет просторан. На внутреннею часть и на внешнюю,которые между собой не прикасаются.замкн. находится,тогда поток вектора E через заданную поверхность Имеется несколько зарядов. Теорема Е —напряженность результирующего поля, а Е i — напряженность поля, создаваемого зарядом Qi. Подставляя последние выражения в, получаем
Б3.Поток вектора напряжённости электрического поля. Теорема Остроградского-Гаусса. Примеры. Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности Ne.
Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).
Поток напряженности через такую элементарную площадку будет равен по определению
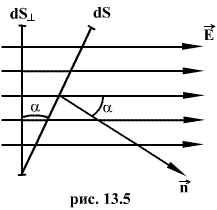
где -a угол между силовой линией и нормалью n к площадке dS; dS - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 5331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.34 (0.008 с.) |

 Если в данной точке пространства различные электрически заряженные частицы 1, 2, 3... и т.д. создают электрические поля с напряженностью Е1, Е2, Е3... и т.д., то результирующая напряженность в данной точке поля равна геометрической сумме напряженностей.
Если в данной точке пространства различные электрически заряженные частицы 1, 2, 3... и т.д. создают электрические поля с напряженностью Е1, Е2, Е3... и т.д., то результирующая напряженность в данной точке поля равна геометрической сумме напряженностей.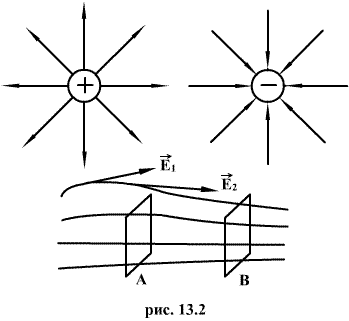
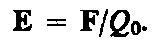 Как следует из формул напряженность поля точечного заряда в вакууме
Как следует из формул напряженность поля точечного заряда в вакууме Векторная сумма -это принцип суперпозиции.Для того чтобы задать поле надо в каждой точке пространства задать направление вектора E и его модуль. Силовая линия -это мысленная кривая.проведенная т. о.,чтобы в каждой точке её вектор E был бы касательной
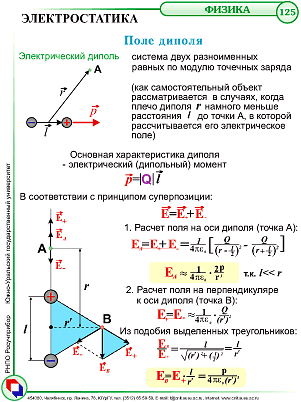
Векторная сумма -это принцип суперпозиции.Для того чтобы задать поле надо в каждой точке пространства задать направление вектора E и его модуль. Силовая линия -это мысленная кривая.проведенная т. о.,чтобы в каждой точке её вектор E был бы касательной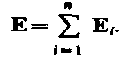 Формула выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя 1. Вектор
Формула выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя 1. Вектор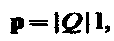 совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом. Согласно принципу суперпозиции напряженность Е поля диполя в произвольной точке
совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом. Согласно принципу суперпозиции напряженность Е поля диполя в произвольной точке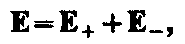 где Е+ и Е– — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.
где Е+ и Е– — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.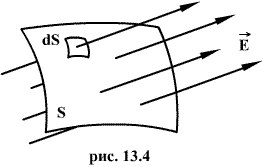
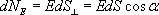
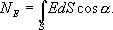 т.к
т.к  то
то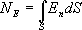 где - En проекция вектора E на нормаль и к поверхности dS.
где - En проекция вектора E на нормаль и к поверхности dS.


