
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт магнитных полей с помощью законаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Расчёт магнитных полей с помощью закона Био–Савара–Лапласа Индукция магнитного поля отрезка прямолинейного проводника с током
Для всех бесконечно малых элементов d l отрезка векторы d l и r лежат в плоскости листа. Поэтому векторы d B, созданные в выбранной нами точке различными элементами проводника направлены одинаково – перпендикулярно плоскости листа. Следовательно, сложение векторов d B можно заменить сложением их модулей d B.
Тогда индукция, созданная элементом проводника dl, равна
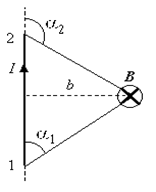
Индукция магнитного поля, созданного всем проводником, может быть найдена как интеграл от dB в пределах от a1 до + a2:
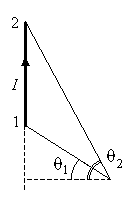
Иногда удобнее воспользоваться другим выражением:
(обратите внимание на рисунок, показывающий углы q1 и q2).
Индукция магнитного поля бесконечно длинного Прямолинейного проводника с током
Если длина прямого проводника бесконечно велика, то a1 = 0, а a2 = p. В этом случае индукция магнитного поля, созданного проводником, будет равна
Дополнительно рассмотрим магнитное поле, созданное бесконечным проводником, который изогнут под прямым углом. Ограничимся получением расчётной формулы для точки А, расположенной на продолжении одной из половин проводника. Участок DB в точке А не создаёт магнитного поля, так как для него a1 и a2 равны 0. Для участка ВС a1 = 900, a2 = -1800. Поэтому индукция, созданная этим участком, равна
Таким образом, индукция магнитного поля в точке А равна половине индукции, созданной прямым бесконечно длинным проводником с таким же током.
Сила Лоренца
Экспериментально установлено, что на заряд, движущийся в магнитном поле, действует сила. Эту силу принято называть силой Лоренца:
Модуль силы Лоренца
где a – угол между векторами v и B. Направление силы Лоренца зависит от направления вектора Дело в том, что сила Лоренца равна результату произведения вектора [ v, В ] на скаляр q. Если заряд положительный, то F л параллельна вектору [ v, В ]. Если же q < 0, то сила Лоренца противоположна направлению вектора [ v, В ] (см. рисунок). Если заряженная частица движется параллельно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен нулю. Следовательно, сила Лоренца на такой заряд не действует (sin 0 = 0, Fл = 0). Если же заряд будет двигаться перпендикулярно силовым линиям магнитного поля, то угол a между векторами скорости и магнитной индукции равен 900. В этом случае сила Лоренца имеет максимально возможное значение: Fл = q v B. Сила Лоренца всегда перпендикулярна скорости движения заряда. Это означает, что сила Лоренца не может изменить величину скорости движения, но изменяет её направление. Поэтому в однородном магнитном поле заряд, влетевший в магнитное поле перпендикулярно его силовым линиям, будет двигаться по окружности. Если на заряд действует только сила Лоренца, то движение заряда подчиняется следующему уравнению, составленному на основе второго закона Ньютона: ma = Fл. Поскольку сила Лоренца перпендикулярна скорости, постольку ускорение заряженной частицы является центростремительным (нормальным): Используя выражение для расчёта ускорения и заменив Fл на q v B, получаем
Отсюда следует, что радиус окружности, по которой будет двигаться заряд в однородном магнитном поле, равен
Если заряженная частица влетит в однородное магнитное поле под углом a к силовым линиям, то её траектория будет более сложной. Для того чтобы установить форму траектории и её параметры, разложим скорость частицы на две компоненты – параллельную v || = vcosa и перпендикулярную v ^= v sina силовым линиям магнитного поля. Компонента скорости v|| не изменяется, так как сила Лоренца не действует на заряженную частицу, движущуюся параллельно силовым линиям магнитного поля. За счёт этой компоненты заряд будет равномерно двигаться вдоль силовых линий.
Заряженная частица одновременно будет участвовать в этих движениях, поэтому её траектория будет представлять собой винтовую линию. Радиус винтовой линии будет равен Период обращения заряженной частицы равен времени, за которое она пройдёт один виток, Шаг винтовой линии равен расстоянию, которое заряд пройдёт за один период: L = v || T. Рассмотрим два одноимённых заряда, движущихся с одинаковой скоростью v вдоль параллельных прямых. За счёт кулоновского взаимодействия они отталкиваются с силой Каждый из зарядов создаёт магнитное поле. Следовательно, на заряды действует сила Лоренца. Заряд q 1 создаёт магнитное поле, индукция которого направлена на нас (см. рисунок), и по модулю равна
Тогда сила Лоренца, действующая на второй заряд, по модулю равна
и направлена так, как показано на рисунке справа. Отношение силы Лоренца к кулоновской силе равно
Значения величин eо и mо связаны между собой соотношением
Таким образом, в рассматриваемой ситуации сила Лоренца меньше кулоновской и возрастает по мере роста скорости движения заряда. Это ещё раз указывает на релятивистский характер магнитного взаимодействия.
Сила Ампера
Если проводник с током поместить в магнитное поле, то на каждый электрон, направленно движущийся в проводнике, действует сила Лоренца. Действие этой силы передаётся всему проводнику. В результате на проводник с током, находящийся в магнитном поле, будет действовать некоторая сила. Найдём её величину. Для этого выделим элементарный участок проводника d l. Результирующая сила d F, действующая на элемент проводника, равна сумме сил, действующих на все электроны в участке d l:
поскольку q. n. v = j, постольку сила d F равна
Это и есть выражение для расчёта силы Ампера, т. е. силы, действующей на элемент проводника с током, находящийся в магнитном поле. Направление силы Ампера совпадает с направлением вектора Для вычисления силы, действующей на весь проводник, необходимо взять интеграл от d F по длине проводника:
Теперь рассмотрим два параллельных проводника с токами I 1 и I 2, расположенных на расстоянии b друг от друга. Первый проводник создаёт магнитное поле, индукция которого
В этом поле на единицу длины второго проводника действует сила, равная
Такая же по величине сила действует и на первый проводник. Легко увидеть, что если токи направлены в одну сторону, проводники притягиваются, если же токи противоположны, то проводники отталкиваются.
В магнитном поле
Рассмотрим контур из П-образного проводника и подвижной перемычки длиной l, находящийся в однородном магнитном поле.
В результате взаимодействия с магнитным полем на перемычку будет действовать сила F = I [ l, B ]. Под действием этой силы перемычка будет двигаться вправо.
При смещении перемычки на dh сила F совершит работу d A = = F d h = I [ l, B ] d h = I B [ d h, l ] = I B d S = IdФ, где dФ = B d S – магнитный поток через элементарную поверхность площадью d S. Магнитным потоком называется скалярная величина, равная скалярному произведению вектора магнитной индукции на площадь элементарной поверхности d S, пронизываемой магнитным полем. Из приведённых выше выкладок видно, что вектор элементарной поверхности d S = [ d h, l ] перпендикулярен поверхности dS и определяется по правилу правого винта для векторного произведения. Размерность магнитного потока [ Ф ] = [ B ][ dS ] = Тл.м2 = Вб Магнитный поток через конечную площадку S равен Ф Таким образом работа, совершаемая при перемещении проводника с током в магнитном поле, определяется выражением
и равна произведению силы тока в проводнике на приращение магнитного потока, вызванное перемещением проводника. В данном случае dФ есть поток вектора магнитной индукции через площадь, пройденную перемычкой в процессе её движения. Теперь рассмотрим жёсткий замкнутый контур с током I, перемещающийся в магнитном поле. Выделим бесконечно малый элемент контура dl. При его перемещении на расстояние dh магнитное поле совершает работу d А ¢ = IdФ ¢, где d А ¢ – работа по перемещению элемента контура dl на расстояние dh, а dФ ¢ – поток вектора магнитной индукции через площадь, пройденную элементом контура dl. Работа по перемещению всего контура на dh
где dФ – магнитный поток через площадь, пройденную всеми элементами контура dl Работа по перемещению контура на конечное расстояние
где Ф 2 и Ф 1 – значения магнитного потока через контур в начальном и конечном положениях контура. Необходимо отметить, что последний результат имеет общий характер, он не зависит от того, как именно изменялось положение контура в пространстве.
Закон полного тока
Рассмотрим магнитное поле, созданное бесконечным прямым проводником с током I. Как было установлено ранее, силовые линии такого тока – окружности с центром на проводнике, а индукция магнитного поля Вычислим для этого поля циркуляцию вектора магнитной индукции Для этого прежде всего необходимо выбрать контур. В данном случае удобнее всего в качестве контура выбрать окружность, совпадающую с сило вой линией магнитного поля. Для так ого контура B d l = Bdl, так как в любой точке В параллелен d l и косинус угла между этими векторами равен единице. Поэтому
Таким образом, циркуляция вектора В оказалась равна произведению магнитной постоянной на ток, охваченный контуром интегрирования:
Можно показать, что полученный результат не связан с формой контура интегрирования и имеет общий характер. Если магнитное поле создано несколькими токами, то индукция магнитного поля в любой точке может быть найдена на основе принципа суперпозиции Циркуляция каждого из векторов В i будет равна произведению силы i -го тока на магнитную постоянную В свою очередь циркуляция вектора В по замкнутому контуру будет равна
т. е. циркуляция вектора магнитной индукции по контуру, охватывающему несколько токов, равна произведению mо на алгебраическую сумму токов, охваченных этим контуром. Полученное выражение для циркуляции вектора магнитной индукции имеет общий характер и называется законом полного тока *.
Знак тока в алгебраической сумме определяется простым правилом: ток, охватываемый контуром, положителен, если его направление совпадает с направлением положитель-ной нормали к контуру (см. рисунок). Направление положительной нормали определяется правилом правого винта: если правый винт вращать по выбранному направлению обхода контура, то направление поступательного движения винта покажет направление положительной нормали n. Закон полного тока удобно использовать для расчёта магнитных полей, созданных токами, которым свойственна симметрия (см. следующий раздел).
Магнитное поле тороида
Тороидом называется соленоид, свёрнутый в кольцо. Поскольку тороид симметричен относительно оси, проходящей через его центр перпендикулярно плоскости, в которой лежит тороид, то и магнитное поле должно быть симметрично относительно этой оси. Следовательно, силовые линии магнитного поля в тороиде также должны быть симметричны относительно той же самой оси. В качестве контура интегрирования удобно выбрать окружность, совпадающую с какой-либо силовой линией магнитного поля. В этом случае циркуляция вектора магнитной индукции Ток, охваченный контуром, Тогда в соответствии с законом полного тока
и
Обратите внимание: магнитная индукция поля внутри тороида зависит от расстояния между центром тороида и точкой внутри него. Величина В обратно пропорциональна расстоянию r. Можно показать, что поле вне тороида равно нулю (примерно так же, как это было сделано в предыдущем разделе для поля вне соленоида).
Индуктивность соленоида
Рассмотрим произвольный замкнутый контур с током I. В соответствии с законом Био–Савара–Лапласа индукция магнитного поля, созданного контуром, прямо пропорциональна силе тока в проводнике. Магнитный поток, охваченный контуром, прямо пропорционален индукции магнитного поля внутри контура и его площади Если охваченная контуром площадь неизменна, то величина магнитного потока прямо пропорциональна В и, следовательно, силе тока в контуре I Ф = LI. Коэффициент пропорциональности L называется коэффициентом индуктивности, или индуктивностью контура. Индуктивность является размерным коэффициентом пропорциональности. В системе СИ размерность индуктивности [ L ] = Гн (генри). Найдём выражение для расчёта индуктивности соленоида. Как показано в разд. 3.11.1, магнитная индукция поля внутри соленоида В = mо nI. Магнитный поток через один виток соленоида Ф = mо nIS = Магнитный поток через N витков соленоида равен Это означает, что для соленоида
и отсюда индуктивность соленоида
где V – объём соленоида. Таким образом, индуктивность соленоида без сердечника определяется плотностью витков и объёмом соленоида.
Магнитное поле в веществе
Магнитное поле создаётся электрическим током. Если один ток создаёт магнитное поле в вакууме, а второй, такой же – в веществе, то созданные ими магнитные поля будут разными. Причём в некоторых веществах магнитное поле будет слабее поля в вакууме, в других – сильнее. По соотношению поля в веществе и в вакууме вещества делят на три класса: диамагнетики, парамагнетики и ферромагнетики. В данном разделе будут рассмотрены причины, по которым разные вещества намагничиваются по-разному.
Намагничивание магнетика
Всякое вещество является магнетиком. Это значит, что всякое вещество способно намагничиваться, т. е. под действием внешнего магнитного поля в нём возникает дополнительное, собственное магнитное поле. Другими словами – индукция магнитного поля внутри магнетика В складывается из индукции внешнего поля В о и индукции собственного поля В¢: В = В о+ В ¢. Механизм намагничивания вещества был раскрыт французским учёным Андре Мари Ампером, который предположил, что во всех молекулах вещества циркулируют круговые токи. Каждый такой ток создаёт магнитное поле. Но, поскольку в отсутствие магнитного поля молекулярные токи ориентируются хаотически, суммарное магнитное поле всех этих токов равно нулю. Появление внешнего магнитного поля вызывает упорядочение ориентации молекулярных круговых токов, в результате чего суммарное магнитное поле молекулярных токов становится отличным от нуля, а магнетик – намагниченным. Намагничивание магнетика количественно характеризуют намагниченностью J, которая определяется выражением
где Размерность вектора намагниченности [ J ] = [ pm ]/[ V ] =
Итак, намагничивание вещества есть результат упорядочивания ориентации молекулярных токов внешним магнитным полем. Условно это можно представить так, как показано на рисунке. Как видно из рисунка, токи внутри объёма магнетика компенсируют друг друга. Токи же, выходящие на боковую поверхность, компенсироваться не будут. Поэтому намагничение вещества можно трактовать как результат появления на боковой поверхности магнетика макроскопического тока намагничивания I ¢.
Магнитомеханические явления
Движение электрона упорядочено. Поэтому орбитальное движение электрона можно трактовать как электрический ток.
Этот круговой ток обладает магнитным моментом pm = IS, направление которого показано на рисунке. Если вещество находится в магнитном поле, на электрон действует вращательный момент M = [ pm, B ] (см. разд. 3.6). Направление вектора момента силы определяется по правилу правого винта для векторного произведения. В данном случае вектор М направлен так, как показано на рисунке справа.
_________________________
*На самом деле циркуляция вектора Н зависит не только от тока проводимости, но и от конвекционного тока (пример – движение заряженных капель дождя) и тока смещения (будет рассмотрен позже) . Расчёт магнитных полей с помощью закона Био–Савара–Лапласа
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.012 с.) |

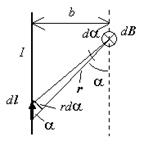
 Из рисунка видно, что r = b /sina
Из рисунка видно, что r = b /sina 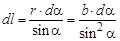 .
.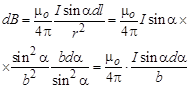 .
.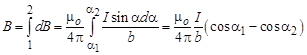
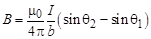
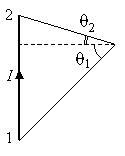 Обратите также внимание на то, что если точка расположена так, как показано на следующем рисунке, то q2 меняет знак и формула для расчёта магнитного поля прямолинейного отрезка записывается следующим образом:
Обратите также внимание на то, что если точка расположена так, как показано на следующем рисунке, то q2 меняет знак и формула для расчёта магнитного поля прямолинейного отрезка записывается следующим образом: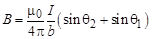 .
.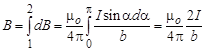 .
.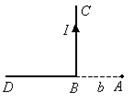 Таким образом, индукция магнитного поля, созданного бесконечно длинным проводником прямо пропорциональна току в проводнике и обратно пропорциональна расстоянию от проводника до интересующей нас точки.
Таким образом, индукция магнитного поля, созданного бесконечно длинным проводником прямо пропорциональна току в проводнике и обратно пропорциональна расстоянию от проводника до интересующей нас точки.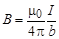 .
. .
.
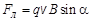 ,
, . Его можно определить с помощью правила правого винта или правила левой руки. Но направление силы Лоренца не обязательно совпадает с направлением вектора
. Его можно определить с помощью правила правого винта или правила левой руки. Но направление силы Лоренца не обязательно совпадает с направлением вектора 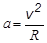 (здесь R – радиус кривизны траектории заряженной частицы).
(здесь R – радиус кривизны траектории заряженной частицы). .
. .
. Компонента скорости v ^ не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость ко-торой перпендикулярна силовым линиям.
Компонента скорости v ^ не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость ко-торой перпендикулярна силовым линиям.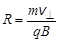 .
. .
. .
. .
.


 .
. , где с – скорость света в вакууме. Поэтому
, где с – скорость света в вакууме. Поэтому .
. .
. ;
; .
. и может быть определено по правилу правого винта для векторного произведения (или по правилу левой руки).
и может быть определено по правилу правого винта для векторного произведения (или по правилу левой руки).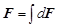 .
. .
.
 .
. Пусть в этом контуре источником ЭДС поддерживается постоянный ток I.
Пусть в этом контуре источником ЭДС поддерживается постоянный ток I.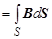 .
. Ф
Ф ,
, ,
, .
. , т. е. интеграл от скалярного произведения вектора магнитной индукции на элемент контура d l, взятый по некоторому замкнутому контуру.
, т. е. интеграл от скалярного произведения вектора магнитной индукции на элемент контура d l, взятый по некоторому замкнутому контуру. .
. .
. , где В i – индукция магнитного поля, созданного i-м проводником с током.
, где В i – индукция магнитного поля, созданного i-м проводником с током. .
.
 ,
,
 (направления В и d l во всех точках контура совпадают, поэтому скалярное произведение B d l равно произведению их модулей; магнитная индукция во всех точках контура одинакова, следовательно, её можно вынести за знак интеграла).
(направления В и d l во всех точках контура совпадают, поэтому скалярное произведение B d l равно произведению их модулей; магнитная индукция во всех точках контура одинакова, следовательно, её можно вынести за знак интеграла).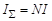 , где N – число витков тороида.
, где N – число витков тороида.
 .
. .
. , где l длина соленоида, N – количество витков соленоида на длине l, S – площадь витка соленоида.
, где l длина соленоида, N – количество витков соленоида на длине l, S – площадь витка соленоида.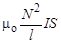 .
.
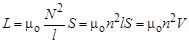 ,
,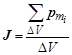 ,
, – суммарный магнитный момент всех молекул, находящихся в элементарном объёме D V в окрестности интересующей нас точки.
– суммарный магнитный момент всех молекул, находящихся в элементарном объёме D V в окрестности интересующей нас точки.
 В атоме любого вещества электроны движутся вокруг ядра. Для объяснения магнитных явлений можно считать, что электрон вращается по круговой орбите. Угловая скорость электрона направлена так, как показано на рисунке (направление можно определить с помощью правила правого винта).
В атоме любого вещества электроны движутся вокруг ядра. Для объяснения магнитных явлений можно считать, что электрон вращается по круговой орбите. Угловая скорость электрона направлена так, как показано на рисунке (направление можно определить с помощью правила правого винта). Электрон движется по круговой орбите, поэтому созданный ток является круговым. Поскольку электрон имеет отрицательный заряд, направление созданного им тока противоположно направлению вращения электрона.
Электрон движется по круговой орбите, поэтому созданный ток является круговым. Поскольку электрон имеет отрицательный заряд, направление созданного им тока противоположно направлению вращения электрона.


