
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о циркуляции вектора НСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть имеется магнетик, находящийся во внешнем магнитном поле. Вычислим циркуляцию вектора магнитной индукции В по некоторому контуру L.
В предыдущем разделе отмечено, что при наличии магнетиков магнитное поле в веществе создаётся не только внешними токами проводимости, но и молекулярными токами I ¢. Поэтому циркуляция вектора магнитной индукции в магнетике будет равна
Учёт молекулярных токов связан с рядом трудностей. Но это затруднение можно устранить. Найдём алгебраическую сумму молекулярных токов, охваченных замкнутым контуром L. Некоторые токи будут дважды пронизывать поверхность, охваченную контуром (см. ток 1 на рисунке). Вклад таких токов в алгебраическую сумму равен нулю. Поэтому в алгебраическую сумму войдут только те токи, которые «нанизаны» на контур (ток 2 на рисунке). Выделим элемент контура длиной dl.
Магнитный момент этого тока равен dI ¢ dS (dS – площадь, охваченная молекулярным током). С другой стороны, магнитный момент можно выразить через намагниченность объёма, занятого эти-ми молекулярными токами, JdV = JdldS. Поэтому можно записать dI ¢ dS = JdldS. Отсюда следует, что dI ¢= Jdl, т. е. элементарный макроскопический ток намагничивания равен произведению намагниченности на элемент контура dl. Интегрируя полученное выражение по контуру L, получаем
Более строгий анализ позволяет получить это выражение в векторной форме
т. е. макроскопический ток намагничивания равен циркуляции вектора намагниченности. Теперь можно записать
Циркуляция величины Как и вектор электрического смещения D в электростатике, Н является вспомогательной характеристикой поля (магнитного). Размерность вектора [ H ] = [ J ] = А/м. Обратите внимание: размерность напряжённости магнитного поля совпадает с размерностью намагниченности. Очевидно, что вещество намагничивается тем сильнее, чем сильнее внешнее магнитное поле. В линейных средах намагниченность J прямо пропорциональна напряжённости внешнего магнитного поля:
J = c H, где c (хи) – магнитная восприимчивость магнетика. Тогда
где m = (1 + c) – магнитная проницаемость вещества. Магнитная проницаемость показывает, во сколько раз индукция магнитного поля в веществе отличается от индукции магнитного поля в вакууме. Последнее соотношение можно переписать в такой форме:
Возвращаясь к расчету циркуляции, можем отметить:
или
т. е. циркуляция вектора напряжённости магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости*, охваченных контуром. Это и есть теорема о циркуляции вектора Н. Эта теорема позволяет осуществлять расчёт магнитного поля в веществе, учитывая только токи проводимости, создающие магнитное поле.
Магнитомеханические явления
Движение электрона упорядочено. Поэтому орбитальное движение электрона можно трактовать как электрический ток.
Этот круговой ток обладает магнитным моментом pm = IS, направление которого показано на рисунке. Если вещество находится в магнитном поле, на электрон действует вращательный момент M = [ pm, B ] (см. разд. 3.6). Направление вектора момента силы определяется по правилу правого винта для векторного произведения. В данном случае вектор М направлен так, как показано на рисунке справа.
_________________________
*На самом деле циркуляция вектора Н зависит не только от тока проводимости, но и от конвекционного тока (пример – движение заряженных капель дождя) и тока смещения (будет рассмотрен позже) .
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.23 (0.01 с.) |


 .
. Молекулярные токи, «нанизанные» на этот элемент контура, создадут элементарный макроскопический ток намагничивания dI ¢ (он равен алгебраической сумме молекулярных токов на элементе контура dl).
Молекулярные токи, «нанизанные» на этот элемент контура, создадут элементарный макроскопический ток намагничивания dI ¢ (он равен алгебраической сумме молекулярных токов на элементе контура dl). .
. ,
, ;
; ;
; .
. не зависит от молекулярных токов. Поэтому её удобно использовать для характеристики магнитного поля в веществе. Эту величину обозначают
не зависит от молекулярных токов. Поэтому её удобно использовать для характеристики магнитного поля в веществе. Эту величину обозначают  и называют напряжённостью магнитного поля Н.
и называют напряжённостью магнитного поля Н. ,
, ,
,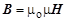 .
. ,
, ,
, В атоме любого вещества электроны движутся вокруг ядра. Для объяснения магнитных явлений можно считать, что электрон вращается по круговой орбите. Угловая скорость электрона направлена так, как показано на рисунке (направление можно определить с помощью правила правого винта).
В атоме любого вещества электроны движутся вокруг ядра. Для объяснения магнитных явлений можно считать, что электрон вращается по круговой орбите. Угловая скорость электрона направлена так, как показано на рисунке (направление можно определить с помощью правила правого винта). Электрон движется по круговой орбите, поэтому созданный ток является круговым. Поскольку электрон имеет отрицательный заряд, направление созданного им тока противоположно направлению вращения электрона.
Электрон движется по круговой орбите, поэтому созданный ток является круговым. Поскольку электрон имеет отрицательный заряд, направление созданного им тока противоположно направлению вращения электрона.


