
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле бесконечного соленоидаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Соленоидом называется проводник, намотанный на цилиндрическую поверхность. Если витки соленоида намотаны вплотную друг к другу, то соленоид удобно представлять в виде совокупности витков одинакового радиуса, расположенных параллельно друг другу вдоль оси соленоида. Центры витков расположены на оси, плоскости витков перпендикулярны оси. Токи во всех витках одинаковы. Как показано в разд. 3.4, вектор магнитной индукции на оси витка параллелен ей. Следовательно, и суммарное поле всех витков на оси соленоида параллельно этой оси. Поскольку соленоид симметричен относительно оси, проходящей через центры витков, постольку и созданное им магнитное поле должно быть симметричным относительно этой оси. Следовательно, магнитное поле параллельно оси соленоида и в остальных точках, расположенных внутри соленоида. Магнитное поле вне бесконечного соленоида равно нулю. Это можно доказать следующим образом.
_______________________
* Иногда этот закон называю т теоремой о циркуляции вектора магнитной индукции. Вначале допустим, что магнитное поле вне соленоида всё же существует.
Для определения индукции магнитного поля вне соленоида воспользуемся законом полного тока. Найдём циркуляцию вектора магнитной индукции по прямоугольному контуру, у которого сторона ab проходит вдоль витков соленоида вблизи от них, а сторона cd находится бесконечно далеко от витков. Скалярное произведение B d l во всех точках сторон bc и da равно нулю, так как угол между В и d l на этих сторонах прямой. Магнитное поле бесконечно далеко от соленоида равно нулю, поэтому вклад участка cd в циркуляцию также равен нулю. Прежде чем определять вклад участка ab, найдём алгебраическую сумму токов, охваченных контуром abcd. Поскольку контур не охватывает ни один виток соленоида, сумма токов равна нулю. Следовательно, и циркуляция вектора В по контуру abcd должна быть равна нулю. Но это означает, что и на участке ab скалярное произведение равно нулю. Это возможно лишь в том случае, если индукция магнитного поля и вблизи от поверхности соленоида равна нулю. Таким образом, магнитное поле вне бесконечно длинного соленоида действительно равно нулю. Теперь найдём индукцию магнитного поля внутри соленоида. В качестве контура интегрирования выберем прямоугольник 1234, две стороны которого параллельны оси соленоида, охватывающий несколько витков соленоида. Циркуляция В по этому контуру равна
Интеграл на участке 3 - 4 также равен нулю, так как поле вне бесконечного соленоида равно нулю. Следовательно, При вычислении интеграла были учтены следующие соображения: – внутри соленоида направление магнитной индукции и направление обхода контура совпадают, поэтому скалярное произведение B d l равно произведению модулей этих векторов; – модуль вектора магнитной индукции во всех точках участка контура 1 - 2 одинаков, поэтому В можно вынести за знак интеграла; – интеграл Ток, охваченный этим контуром, равен nl 12 I, где n – количество витков на единице длины соленоида, I – ток в одном витке. На основе закона полного тока циркуляция вектора магнитной индукции равна произведению mо на алгебраическую сумму токов, охваченных контуром, Bl 12 = mo nl 12 I; сокращая длину участка 1 - 2, получаем выражение для расчёта индукции магнитного поля внутри бесконечного соленоида: B = mo nI. Обратите внимание на то, что величина В внутри соленоида не зависит от расстояния между точкой и осью соленоида. Это значит, что магнитное поле внутри бесконечного соленоида однородно.
Магнитное поле тороида
Тороидом называется соленоид, свёрнутый в кольцо. Поскольку тороид симметричен относительно оси, проходящей через его центр перпендикулярно плоскости, в которой лежит тороид, то и магнитное поле должно быть симметрично относительно этой оси. Следовательно, силовые линии магнитного поля в тороиде также должны быть симметричны относительно той же самой оси. В качестве контура интегрирования удобно выбрать окружность, совпадающую с какой-либо силовой линией магнитного поля. В этом случае циркуляция вектора магнитной индукции Ток, охваченный контуром, Тогда в соответствии с законом полного тока
и
Обратите внимание: магнитная индукция поля внутри тороида зависит от расстояния между центром тороида и точкой внутри него. Величина В обратно пропорциональна расстоянию r. Можно показать, что поле вне тороида равно нулю (примерно так же, как это было сделано в предыдущем разделе для поля вне соленоида).
Индуктивность соленоида
Рассмотрим произвольный замкнутый контур с током I. В соответствии с законом Био–Савара–Лапласа индукция магнитного поля, созданного контуром, прямо пропорциональна силе тока в проводнике. Магнитный поток, охваченный контуром, прямо пропорционален индукции магнитного поля внутри контура и его площади Если охваченная контуром площадь неизменна, то величина магнитного потока прямо пропорциональна В и, следовательно, силе тока в контуре I Ф = LI. Коэффициент пропорциональности L называется коэффициентом индуктивности, или индуктивностью контура. Индуктивность является размерным коэффициентом пропорциональности. В системе СИ размерность индуктивности [ L ] = Гн (генри). Найдём выражение для расчёта индуктивности соленоида. Как показано в разд. 3.11.1, магнитная индукция поля внутри соленоида В = mо nI. Магнитный поток через один виток соленоида Ф = mо nIS = Магнитный поток через N витков соленоида равен Это означает, что для соленоида
и отсюда индуктивность соленоида
где V – объём соленоида. Таким образом, индуктивность соленоида без сердечника определяется плотностью витков и объёмом соленоида.
Магнитное поле в веществе
Магнитное поле создаётся электрическим током. Если один ток создаёт магнитное поле в вакууме, а второй, такой же – в веществе, то созданные ими магнитные поля будут разными. Причём в некоторых веществах магнитное поле будет слабее поля в вакууме, в других – сильнее. По соотношению поля в веществе и в вакууме вещества делят на три класса: диамагнетики, парамагнетики и ферромагнетики. В данном разделе будут рассмотрены причины, по которым разные вещества намагничиваются по-разному.
Намагничивание магнетика
Всякое вещество является магнетиком. Это значит, что всякое вещество способно намагничиваться, т. е. под действием внешнего магнитного поля в нём возникает дополнительное, собственное магнитное поле. Другими словами – индукция магнитного поля внутри магнетика В складывается из индукции внешнего поля В о и индукции собственного поля В¢: В = В о+ В ¢. Механизм намагничивания вещества был раскрыт французским учёным Андре Мари Ампером, который предположил, что во всех молекулах вещества циркулируют круговые токи. Каждый такой ток создаёт магнитное поле. Но, поскольку в отсутствие магнитного поля молекулярные токи ориентируются хаотически, суммарное магнитное поле всех этих токов равно нулю. Появление внешнего магнитного поля вызывает упорядочение ориентации молекулярных круговых токов, в результате чего суммарное магнитное поле молекулярных токов становится отличным от нуля, а магнетик – намагниченным. Намагничивание магнетика количественно характеризуют намагниченностью J, которая определяется выражением
где Размерность вектора намагниченности [ J ] = [ pm ]/[ V ] =
Итак, намагничивание вещества есть результат упорядочивания ориентации молекулярных токов внешним магнитным полем. Условно это можно представить так, как показано на рисунке. Как видно из рисунка, токи внутри объёма магнетика компенсируют друг друга. Токи же, выходящие на боковую поверхность, компенсироваться не будут. Поэтому намагничение вещества можно трактовать как результат появления на боковой поверхности магнетика макроскопического тока намагничивания I ¢.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1081; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.170.65 (0.007 с.) |

 Тогда оно должно быть симметричным относительно оси соленоида. Это значит, что силовые линии магнитного поля вне соленоида должны быть параллельны его оси.
Тогда оно должно быть симметричным относительно оси соленоида. Это значит, что силовые линии магнитного поля вне соленоида должны быть параллельны его оси.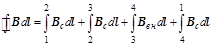
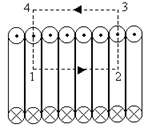 На участках 2 - 3 и 4 - 1 индукция поля в соленоиде В с перпендикулярна элементу контура dl, поэтому скалярное произведение В с и d l равно нулю.
На участках 2 - 3 и 4 - 1 индукция поля в соленоиде В с перпендикулярна элементу контура dl, поэтому скалярное произведение В с и d l равно нулю. , где l 12 – длина стороны 1 - 2 контура интегрирования.
, где l 12 – длина стороны 1 - 2 контура интегрирования. , поэтому циркуляция равняется произведению модуля магнитной индукции на длину участка 1 - 2.
, поэтому циркуляция равняется произведению модуля магнитной индукции на длину участка 1 - 2. (направления В и d l во всех точках контура совпадают, поэтому скалярное произведение B d l равно произведению их модулей; магнитная индукция во всех точках контура одинакова, следовательно, её можно вынести за знак интеграла).
(направления В и d l во всех точках контура совпадают, поэтому скалярное произведение B d l равно произведению их модулей; магнитная индукция во всех точках контура одинакова, следовательно, её можно вынести за знак интеграла).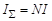 , где N – число витков тороида.
, где N – число витков тороида.
 .
. .
. , где l длина соленоида, N – количество витков соленоида на длине l, S – площадь витка соленоида.
, где l длина соленоида, N – количество витков соленоида на длине l, S – площадь витка соленоида.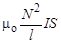 .
.
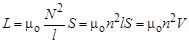 ,
,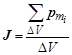 ,
, – суммарный магнитный момент всех молекул, находящихся в элементарном объёме D V в окрестности интересующей нас точки.
– суммарный магнитный момент всех молекул, находящихся в элементарном объёме D V в окрестности интересующей нас точки.



