Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поля соленоида, тороида, прямолинейного токаСодержание книги
Поиск на нашем сайте
Соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник c током I. Длина соленоида l содержит N витков и по нему протекает ток I. Считаем соленоид бесконечно длинным. Внутри соленоида поле однородно, а вне соленоида не однородно и очень слабое (можно считать, равным нулю). РИСУНОК Bвнутри>>Bснаружи~0. Вспомогательный контур выбирают в виде прямоугольника l*h. Тогда по теореме о циркуляции B*l+0+Bвне*l+0=μ0*N*I; B= μ0*N*I/l= μ0*n*I, n=N/l – число витков на единицу длины соленоида Тороид можно рассматривать как длинный соленоид, свернутый в кольцо, на который равномерно намотаны витки провода. РИСУНОК Магнитное поле внутри тороида, так же, как в соленоиде, однородно, сосредоточено внутри; вне тороида магнитное поле, создаваемое круговыми токами тороида, равно нулю. По т. о циркуляции B*2*π*R= μ0*N*I; B= μ0*N*I/(2*π*R) То есть соленоид создает дополнительное магнитное поле, такое же, как и прямолинейный бесконечно длинный проводник с током. Точно так же и для тороида: вдоль средней линии протекает эффективный ток I. где μ — магнитная проницаемость среды, μ0 = 4 23. Сила Лоренца.Сила Ампера Отношение сил Fмагн/Fк=μ0*V^2*ε0/1=V^2/c^2<<1 при обычных условиях. Пусть по тонкому сечению S проводника протекает ток I=j*S=e*n*u*S; заряд, протекающий по участку dl, dq=e*n*S*dl=e*n*dV=e*dN. При наличии магн.поля на этот заряд и соответственно на участок проводника действует сила Ампера. d Получаем выражение для силы, действующей на участок тонкого проводника с током, со стороны магнитного поля.
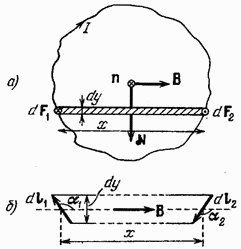
Контур с током в магнитном поле Выясним, как ведет себя контур с током в однородном магнитном поле. На элемент контура действует сил
Таким образом, результирующая сила, действующая на контур с током в однородном магнитном поле, равна нулю. Рассмотрим плоский контур. Рез-ий момент относ. некот. точки О определяется выражением
Просуммировав это выражение по всем полоскам, получим вращательный момент, действующий на контур:
Получим выражение для пот. энергии дип магн момента в магн поле:
Для того чтобы угол а между векторами
Работа (46.9) идет на увеличение потенциальной энергии
Интегрируя, находим
Параллельная ориентация векторов и В отвечает минимуму энергии (46.10) и, следовательно, положению устойчивого равновесия контура. Намагничение магнетика Если несущие ток провода находятся в какой-либо среде, магнитное поле изменяется. Это объясняется тем, что всякое вещество является магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле В, которое накладывается на обусловленное токами поле Во. Оба поля в сумме дают результирующее поле
Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается — его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле Намагничение магнетика хар-ся магнитным моментом единицы объема. Эту величину называют намагниченностью и обозначают буквой J. Поле В, так же как и поле
Таким образом, формула (49.2), а следовательно, и формула (49.1) справедливы не только для поля в вакууме, но и для поля в веществе.
26. Условие на границе 2 магнетиков Основными уравнениями магнитостатики при наличии магнетиков являются:
При переходе из одной среды в другую магнитная проницаемость претерпевает скачок, соответственно вектора Это изменение определяется с помощью теоремы Гаусса и по циркуляции. Пусть участок границы площади S охватывает замкнутый цилиндр высоты dh->0: Тогда поток вектора
Нормальная составляющая вектора Выделим у границы раздела прямоугольник dh* Теорема о циркуляции дает:
Предполагаем, что токи проводимости на границе раздела отсутствуют Cледовательно,
27. Явление электромагнитной индукции. ЭДС индукции При изменении магнитного потока через поверхность, ограниченную замкнутым проводящим проводом, возникает электр. ток, который называют индукционным. Следовательно, в контуре действует электродвижущая сила. Это явление электромагнитной индукции. Количественно явление описывается законом электромагнитной индукции:
ЭДС индукции равна скорости изменений магнитного потока через поверхность, взятого с обратным знаком. Знак “—” отражает правило Ленца:
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 ·10-7 H/A2 — магнитная постоянная, I — сила тока в проводнике, r — расстояние от проводника до точки, в которой вычисляется магнитная индукция.
·10-7 H/A2 — магнитная постоянная, I — сила тока в проводнике, r — расстояние от проводника до точки, в которой вычисляется магнитная индукция.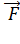 =q*[
=q*[ 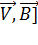 ; F=q*V*B*sinα;
; F=q*V*B*sinα;  _|_
_|_  à
à 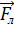 =q*
=q* 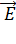 +q*[
+q*[  =dq*[
=dq*[  =e*n*S*dl*[
=e*n*S*dl*[ 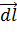 ↑↑
↑↑  , d
, d  . РИСУНОК
. РИСУНОК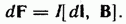

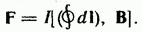 =0
=0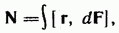 где r — радиус-вектор, проведенный из точки О в точку приложения силы dF. Возьмем точку О, смещенную относительно О на отрезок Ь.
где r — радиус-вектор, проведенный из точки О в точку приложения силы dF. Возьмем точку О, смещенную относительно О на отрезок Ь.
 Моменты, вычисленные относ. двух произвольно взятых точек О и О', оказались совпадающими. Отсюда заключаем, что момент не зависит от выбора точки, относительно которой он берется (ср. с парой сил).
Моменты, вычисленные относ. двух произвольно взятых точек О и О', оказались совпадающими. Отсюда заключаем, что момент не зависит от выбора точки, относительно которой он берется (ср. с парой сил).


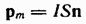 -дипольным магнитным моментом контура с током. Направление вектора
-дипольным магнитным моментом контура с током. Направление вектора  совпадает с направлением положительной нормали к контуру.
совпадает с направлением положительной нормали к контуру.  При B||n, M=0 всегда.
При B||n, M=0 всегда.
 увеличить на
увеличить на  нужно совершить против сил, действующих на контур в магнитном поле, работу
нужно совершить против сил, действующих на контур в магнитном поле, работу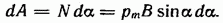
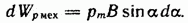

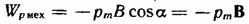 (46.10)
(46.10)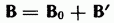
 .
.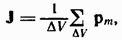
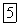 не имеет источников. Поэтому дивергенция результирующего поля (51.1) равна нулю:
не имеет источников. Поэтому дивергенция результирующего поля (51.1) равна нулю: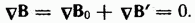
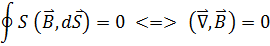
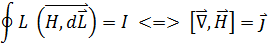

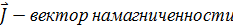
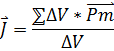

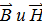 изменяются скачкообразно.
изменяются скачкообразно.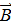 :
:

 испытывает скачок.
испытывает скачок.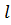 :
: