
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрический заряд. Закон кулона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЭЛЕКТРИЧЕСКИЙ ЗАРЯД. ЗАКОН КУЛОНА. Электрический заряд характеризует способность тел к электромагнитному взаимодействию.
В СИ коэффициент пропорциональности равен k=1/(4pe0). Тогда закон Кулона запишется в окончательном виде:
НАПРЯЖЕННОСТЬ ПОЛЯ. ПОТЕНЦИАЛ. Взаимодействие между неподвижными зарядами осуществляется посредством электрического поля. Заряды создают в окруж. Пространстве эл.полеб которое обнаруживается по его воздействию на другие заряды. Количественными характеристиками эл.поля являются векторная величина напряженность Е(1В/м) и сколярная величина потелниал ф(1В). Пусть эл.поле создает система зарядов q1,q2…qn. Сила, с которой эта система действует на пробный заряд q0 равна E-силовая хар-тика эл.поля, зная Е можно найти силу, действующую на заряд, помещенный в это поле. Для напряженности выполняется принцип суперпозиции: напряженность поля системы зарядов равна векторной сумме напряженностей полей создаваемых каждым зарядом взятым поотдельности. Выражения длс напряженности точечного заряда ( Потенциал – энерг.характеристика поля, т.к. зная его можно найти потенциальную энергию точечного заряда q (W=qф) Любая работа, которая будет совершаться полем, будет происходить за счет уменьшения потенциальной энергии.
В случае если поле создается несколькими зарядами, которые расположены в произвольном порядке. Потенциал в данной точке такого поля будет представлять собой алгебраическую сумму всех потенциалов, которые создают заряды каждый в отдельности. Это так называемый принцип суперпозиции.
ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ СИСТЕМЫ ЗАРЯДОВ Рассмотрим энергию взаимодействия точенных зарядов. Сначала ограничимся случаем двух точечных зарядов q1 и q2. Энергия заряда q1 в поле заряда q2 может быть определена выражением где фi – потенциал, создаваемый в месте нахождения i -го заряда системой, за исключением этого i -го заряда.
ДИПОЛЬ. ПОЛЕ ДИПОЛЯ. Электрическим диполем называется система двух одинаковых по величине разноимённых точечных зарядов +q и –q, на расстоянии l между которыми значительно меньше расстояния до тех точек, в которых определяется поля системы. Прямая, проходящая через оба заряда, называется осью диполя. Поле диполя обладает осевой симметрией. Поэтому вид поля в любой плоскости, проходящей через ось диполя, будет одной и той же, причём вектор E лежит в этой плоскости. С учетом неравенства сможем записать
Потенциал эл.поля, создаваемого диполем в точке
ГРАДИЕНТ.ДИВЕРГЕНЦИЯ.РОТОР. 1)градиент Пусть задано скалярное поле ф(r)=ф(x,y,z). Рассмотрим приращение скалярного поля dф при перемещении dl=dxi+dyj+dzk от точки, радиус-вектор которой r,(r+dl) Тогда 2)дивергенция:Под потоком понимают объем жидкости протекающей через некотор выделенную поверхность в 1 времени.Отличие потока от нуля через замкнутую поверхность означает наличие источников или стоков жидкости. Величина Ф определяет суммарную алгебраическую мощность источников в объем V. 3) ротор:Аддитивность циркуляции позволяет ввести понятие удельной циркуляции, т.е. отношение с к величине поверхности S. При конечных размерах S отношение с/S дает среднее значение удельной циркуляции.В точке поле будет характеризовать выражение:
Поляризуемость молекулы. В результате любой объём V диэлектрика приобретает дипольный момент. В результате поляризации диэлектрика на его поверхности и по объёму возникают заряды Отличают сторонние и связанные заряды. Обозначают q(ст) и q’(связ). Сторонние заряды – это заряды, которые мы можем заряжать и перемещать. Связанные – это заряды, возникшие в результате смещения зарядов диэлектрика в пределах своих молекул. Связанные заряды наряду со сторонними создают эл.поле. В результате мы наблюдаем Выберем в изотопном диэлектрике некоторую поверхность S и вычислим заряд q’, прошедший через эту пов-сть, при включении внешнего эл.поля. Выделяем площадку Очевидно, что все положительные заряды, находящиеся в пределах цилиндра с основанием Заряд, прошедший через dS в направлении нормали, в результате поляризации dq’=( Пусть S – замкнутая пов-сть. Тогда из объёма, ограниченного этой пов-стью, вышел q св q’ выш. = Вблизи пов-сти, вблизи границы диэлектрика выделим dS*dh РИСУНОК Появился заряд dq’=( Несимметричные молекулы NH, HCl, CO изначально обладают дипольным моментом Диэлектрические ионные кристаллы состоят из двух подрешёток: положительной и отрицательной, которые сдвигаются при включении внешнего поля. В результате возникает ненулевой вектор Выясним, когда в диэлектрике возникают объёмные связанные заряды: поле создаётся как сторонними, так и связанными зарядами, поэтому для E следует записать т.Гаусса (набла,Е)=(ρ+ρ’)/ε0; (набла, Ненулевая объёмная ρ связ.зарядов возникает в поляр. диэлектрике,если: 1)диэлектрик не однороден, т.е. (набла, χ) не равно 0 2)по V диэлектрика распределён сторонний заряд
Проводники в эл поле В металлических проводниках имеются свободные носители заряда – электроны проводимости (свободные электроны), которые могут под действием внешнего электрического поля перемещаться по всему проводнику. Поэтому в проводниках должны выполн.след.условия: 1)Евнутри=0. Вызывало бы движ.своб.зарядов 2)Напряж.поля у пов-сти проводника _|_ его пов-сти 3)Потенциал всех точек проводника одинаков 4)Т.к. (набла,Е)=ро/эпс0, Е=0, то ро=0 В силу отсутствия заряда внутри проводника ничто не изменится с точки зрения осн. ур-ий эл/стат., если внутри проводника сущ. полость без заряда. Напряж.поля у пов-сти проводника связана с пов. плотностью заряда. На пов-сти проводника выделяют небольшой участок пов-сти S такой, чтобы его можно было считать пллоским. Выберем такую пов-сть с основаниями S, лежащими на проводнике, на высоте h<<√S, Eвнутри=0, Евне_|_пов-сти По т.Гаусса поток Фе=Е*S+0+0=σ*S/ε0àE= σ/ε0, E(à)=σ*n(à)/ε0 Поле создаётся при h<<√S. Пов-сть S можно считать бесконечной плоскостью, создающей поле напряжённости Е1=σ/(2*ε0) Остальная пов-сть проводника создаёт поле такое, что Е2=Е1, Е=Е1+Е2= σ/ε0 *n(à) На участке S, заряд которого σ*S, действует только напряжённость Е2, F=σ*S* σ*n(à)/(2* ε0) Значит,давление P= σ^2/(2* ε0)
15 .Электроемкость уединенного проводника. Конденсаторы Конденсатор – это система из двух (иногда более) проводников (обкладок) с одинаковыми по модулю, но противоположными по знаку зарядами. Емкость конденсатора – это физическая величина, равная отношению заряда q, расположенного на положительно заряженной обкладке конденсатора, к разности потенциалов фи1-фи2 между его обкладками. U=фи1-фи2 - напряжение, приложенное к конденсатору. Для плоского конденсатора C=(e*e0*S)/d при парал-ом соединении конденсаторов полная емкость будет равна сумме емкостей отдельных конденсаторов, при последовательном соединении конденсаторов суммируются обратные величины емкостей Уединенным проводником называется проводник, который находится настолько далеко от других тел, что влиянием их электрических полей можно пренебречь. Характер распределения зарядов по поверхности заряженного уединенного проводника, находящегося в однородной, изотропной диэлектрической среде, зависит только от формы поверхности проводника. Поверхностная плотность зарядов в каждой точке поверхности проводника пропорциональна его общему заряду: сигма=kq Опыт показывает, что заряд q на уединенном проводнике прямо пропорционален его потенциалу фи. Коэффициент пропорциональности С называется электрической емкостью (электроемкостью или просто емкостью) этого проводника С=q/фи (фарад) Емкость зависит от формы и размера уединенного проводника и от диэлектрических свойств окружающей среды
ЭДС. ЗАКОНЫ ОМА Для существования тока в проводнике необходимо наличие ненулевого эл.поля. Оно создаётся за счёт некоторого распределения заряда вследствие движения положит.носителей из точек с большим потенциалом в точки с меньшим. Поле быстро исчезает, и ток прекращается. Для его поддержания необходимо существование сил неэлектростатического происхождения, которые переносили бы положительные носители из точек с меньшим φв точки с большим. РИСУНОК Эти силы называют сторонними, т.к. они имеют эл/магн природу, так же они пропорциональны переносимому заряду. ЭДС1,2 = Астор /q = Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних сил в источниках постоянного или переменного тока. На участке цепи действует сила I= Если действуют сторонние силы, то следует написать: заряды движ. за счёт эл.поля и стор.сил: Пусть по цепи протекает постоянный ток I, за время t переносится заряд q=I*t на некотором участке цепи 1-2, силы эл/стат поля и сторонние совершают работу А12=q*U12=I*U12*t, называемая работой тока. Мощность P=I*U12. Эта работа идёт на увеличение внутренней энергии проводника, хим.реакции, на работу по перемещению проводника. Если проводник однороден и неподвижен, то вся работа тока идёт на нагревание. Согласно экспериментальному закону, количество теплоты, выделяющейся при прохождении тока, =I^2*R*t – закон Джоуля-Ленца. В случае однородного неподвижного проводника выполняется закон Ома. Для небольшого цилиндрического проводника I=j*dS_|_, R=ρ*dl/dS_|_, Q=j^2*(dS_|_)^2* ρ*dl/ (dS_|_)= ρ* j^2*dV*t. Удельная тепловая мощность Q= ρ* j^2
Намагничение магнетика Если несущие ток провода находятся в какой-либо среде, магнитное поле изменяется. Это объясняется тем, что всякое вещество является магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле В, которое накладывается на обусловленное токами поле Во. Оба поля в сумме дают результирующее поле
Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается — его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле Намагничение магнетика хар-ся магнитным моментом единицы объема. Эту величину называют намагниченностью и обозначают буквой J. Поле В, так же как и поле
Таким образом, формула (49.2), а следовательно, и формула (49.1) справедливы не только для поля в вакууме, но и для поля в веществе.
26. Условие на границе 2 магнетиков Основными уравнениями магнитостатики при наличии магнетиков являются:
При переходе из одной среды в другую магнитная проницаемость претерпевает скачок, соответственно вектора Это изменение определяется с помощью теоремы Гаусса и по циркуляции. Пусть участок границы площади S охватывает замкнутый цилиндр высоты dh->0: Тогда поток вектора
Нормальная составляющая вектора Выделим у границы раздела прямоугольник dh* Теорема о циркуляции дает:
Предполагаем, что токи проводимости на границе раздела отсутствуют Cледовательно,
27. Явление электромагнитной индукции. ЭДС индукции При изменении магнитного потока через поверхность, ограниченную замкнутым проводящим проводом, возникает электр. ток, который называют индукционным. Следовательно, в контуре действует электродвижущая сила. Это явление электромагнитной индукции. Количественно явление описывается законом электромагнитной индукции:
ЭДС индукции равна скорости изменений магнитного потока через поверхность, взятого с обратным знаком. Знак “—” отражает правило Ленца: Вихревое электрическое поле Магнитный поток через поверхность ограниченную замкн. проводящим контуром, может изменяться за счёт изменения индукции магнитного поля В при неподвижном конуре. В этом случае также возник. ЭДС индукции Для объяснения возник. Максвелл предположил, что E возникает во всём пространстве при изменении B и не зависит от наличия замкнутого проводящего контура. Контур служит для обнаружения возникшего электр. поля. Поэтому контур L выбирается как воображаемый контур. Для выполнения последнего равенства следует положить [набла,Е]=-∂B/∂t В отличие от электростатики, когда заряды неподвижны, электр. поле может быть вихревым, не потенциальным. В интегральной форме эквивалентное уравнение имеет вид:
Ток смещения Одним из основных уравнений магнитостатики явл. Максвелл предположил,что уравнение для напряжённости магн. поля H следует писать в виде Должно выполн. Таким образом плотность тока смещения С учётом плотности тока смещения т. О циркуляции для H в диф. Формуле запишется Ток смещения Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
Выражение (138.2) и было названо Максвеллом плотностью тока смещения. Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле В диэлектриках ток смещения состоит из двух слагаемых. Так как, согласно (89.2), D =e0 E + P, где Е — напряженность электростатического поля, а Р — поляризованность (см. § 88), то плотность тока смещения
в вакууме, д P / д t — плотность тока поляризации — тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах). Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по своей природе не отличаются от токов проводимости. Однако то, что и другая (e0 д E / д t), часть плотности тока смещения (e0 д E / д t), не связанная с движением зарядов, а обусловленная только изменением электрического поля во времени, также возбуждает магнитное поле, является принципиально новым утверждением Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возникновению в окружающем пространстве магнитного поля.
УРАВНЕНИЕ МАКСВЕЛЛА Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Основу электромагнитной теории света максвелла образуют уравнения максвелла. Первая пара уравнений максвелла
Интерференция световых волн Световые волны представляют собой часть спектра э/м волн. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями эл.вектора Е. Поэтому вектор Е называют световым вектором. Его поведение даётся выражением Среда с большим значением n называется более оптически плотной. Видимому диапазону света соответствуют длины волн λ=0.4-0.76 мкм; V=c/ λ0 Пусть 2 волны одной частоты, накладываясь друг на друга, возбуждают колебания. Согласно принципу суперпозиции, мы наблюдаем колебания
В случае сложения когерентных волн интенсивность не равна сумме интенсивностей волн, а будет меняться при переходе от одной т. пространства в другую, т.к. -1<= cosδ<=1. Это явление называют интерференцией. Происходит распределение интенсивности света в пространстве; в результате возникают чередующиеся max и min интенсивности. Естественные источники света некогерентны, поэтому для наблюдения интерференции поступают след.образом: С помощью отражений и преломлений пучок света разбивают на 2 пучка,которые проходят различные пути s1, s2 в средах с показателем преломления n1, n2, а затем сводят их вместе РИСУНОК Если закон A*cos(w*t), то в т.Р приходят колебания A1*cos(w*(t-s1/v1)) и A2*cos(w*(t-s2/v2)). S=w*s1/v1-w*s2/v2=(w/c)*(n1*s1-n2*s2)=(2*π/λ0)*(n1*s1-n2*s2) Разность фаз определяется оптической разностью хода ∆= n1*s1-n2*s2; δ=(2*π/λ0)* ∆ Максимумы интенсивности будет наблюдаться при условии δ=+-2*π*m; ∆=+-m* λ0=+-2*m* λ0/2 Минимумы интенсивности наблюдаются при δ=+-(2*m+1)*π или ∆=+-(2*m+1)* λ0/2 Интерференцию в лаб.условиях наблюдал Юнг. Слабый пучок света падал на экран с двумя близко расположенными отверстиями, интерференция наблюдалась на другом параллельном экране РИСУНОК Тогда разность хода ∆ =s2-s1=d*sinθ=d*tgθ=d*x/l Оптическая разность тока ∆=n*dx/làусловие наблюдения максимумов на экране будет n*dxmax/l=+-m* λ0 и минимумов n*dxmin/l=+-(m+0.5)* λ0. Видно, что расстояние между соседними максимумами одинаково ∆х=l/d * λ0/n=l* λ/d. На экране max и min равномерно чередуются. При естественном предположении равенства интенсивности двух лучей для результирующей интенсивности получаем:
Max интенсивности в 4 раза больше интенсивности одного луча. Зная геометрию установки, по измеренному dx можно определить длину волны падающего света
Многолучевая интерференция Пусть в некоторой точке Р есть несколько когерентных световых лучей, фазы которых сдвинуты отн. друг друга на одну и ту же величину ∆ E1=a*cos(w*t), E2=a*cos(w*t+δ); En=a*cos(w*t+(N-1)*δ) Амплитуду результ. колебания найдём,воспользовавшись векторной диаграммой РИСУНОК Точки, определяющие начало и концы слагаемых векторов, лежат на окружности, радиус которой = a/(2*sin(δ/2)) à амплитуда результирующего колебания A=2*R*sin(N*δ/2)=a* sin(N*δ/2)/sin(δ/2) Интенсивность волны прямопропорциональна квадрату А колебаний. Для одной волны I0=k* Интенсивность главных максимумов света возрастает в 0<δ<2πà0<N*δ/2<k*π<N*π В промежутках между двумя главными максимумами находится N-2 дополнительных максимума. Интерференция большого числа лучей наблюдается в интерферометре Фабри-Перро - тонкий воздушный слой между двумя плоско-параллельными пластинками Дифракция на диске.
В точке Р в центре геометрической тени всегда наблюдается интерференционный максимум, называемый пятном Пуассона, соответствующий половине действия только первой (m + 1) открытой зоны Френеля, и окруженный концентрическими с ним темными и светлыми кольцами. Дифракционная решетка
b - ширина щели; а - ширина непрозрачного участка; d = a + b - период решетки.
Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция. Т.к. щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки.
В направлениях, в которых наблюдается минимум для одной щели, будут минимумы и в случае N щелей, т.е. условие главных минимумов дифракционной решетки будет аналогично условию минимумов для щели:
40. (2) - условие главных минимумов. Условие максимумов; те случаи φ, которые удовлетворяют максимумам для одной щели, могут быть либо максимумами, либо минимумами, т.к. всё зависит от разности хода между лучами. Условие главных максимумов:
Эти максимумы будут расположены симметрично относительно центрального (нулевого k = 0) максимума. Для тех углов φ, для которых одновременно выполняется (2) и (3) максимума не будет, а будет минимум (например, при d =2b для всех четных k =2 р, р = 1, 2, 3...). Между главными максимумами имеются дополнительные очень слабые максимумы, интенсивность которых во много раз меньше интенсивности главных максимумов (1/22 интенсивности ближайшего главного максимума). Дополнительных максимумов будет N - 2, где N - число штрихов. Условие дополнительных максимумов: | ||
|
| Поделиться: |

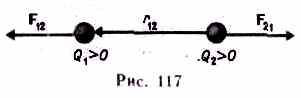
 Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними:
Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними: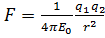
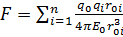
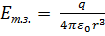 ) и принцип суперпозиции позволяют вычислить напряженность системы зарядов. Работа, совершаемая силами эл.поля создаваемого неподвижным точечным зарядом может быть представлена как убыль потенциальной энергии заряда q0
) и принцип суперпозиции позволяют вычислить напряженность системы зарядов. Работа, совершаемая силами эл.поля создаваемого неподвижным точечным зарядом может быть представлена как убыль потенциальной энергии заряда q0 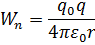
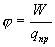
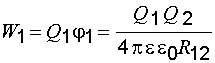 где
где 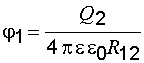 – потенциал, создаваемый вторым зарядом в месте нахождения первого заряда. С другой стороны, энергия заряда q2 может быть определена аналогичным выражением
– потенциал, создаваемый вторым зарядом в месте нахождения первого заряда. С другой стороны, энергия заряда q2 может быть определена аналогичным выражением 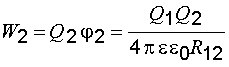 где ф2 – потенциал, создаваемый первым зарядом в месте нахождения первого заряда. Получаем, что энергии равны W1=W2=W (– энергия взаимодействия зарядов q1 и q2), однако формулы, описывающие энергию взаимодействия через заряд и потенциал, не симметричны относительно индексов 1 и 2. Чтобы сделать формулу, описывающую энергию взаимодействия зарядов, симметричной относительно индексов, перепишем ее следующим образом:
где ф2 – потенциал, создаваемый первым зарядом в месте нахождения первого заряда. Получаем, что энергии равны W1=W2=W (– энергия взаимодействия зарядов q1 и q2), однако формулы, описывающие энергию взаимодействия через заряд и потенциал, не симметричны относительно индексов 1 и 2. Чтобы сделать формулу, описывающую энергию взаимодействия зарядов, симметричной относительно индексов, перепишем ее следующим образом: 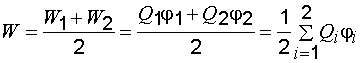 В общем случае, когда система содержит n точечных зарядов, энергия взаимодействия этих зарядов может быть описана формулой, которая получается обобщением предыдущей формулы
В общем случае, когда система содержит n точечных зарядов, энергия взаимодействия этих зарядов может быть описана формулой, которая получается обобщением предыдущей формулы 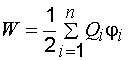
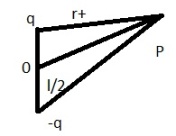
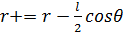
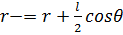
 Электрический дипольный момент
Электрический дипольный момент 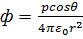 . Напряженность поля определим по проекциям на направление задаваемое изменением R:
. Напряженность поля определим по проекциям на направление задаваемое изменением R: 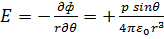
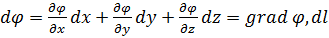 Градиент скалярной функции позволяет найти ее приращение при перемещении dl
Градиент скалярной функции позволяет найти ее приращение при перемещении dl 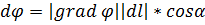
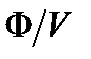 -средняя мощность источников.При V ® 0 — удельная мощность точки P,ее называют дивергенцией (расхождением ) вектора
-средняя мощность источников.При V ® 0 — удельная мощность точки P,ее называют дивергенцией (расхождением ) вектора 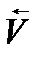 :
: 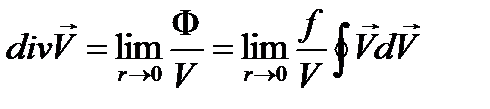 Интеграл берется по любой замкнутой поверхности, содержащей точку V. В декартовых координатах,
Интеграл берется по любой замкнутой поверхности, содержащей точку V. В декартовых координатах,  ;
; где с – циркуляция вектора по контуру Г, S – площадь контура. В одной и той же точке Р для разных
где с – циркуляция вектора по контуру Г, S – площадь контура. В одной и той же точке Р для разных 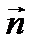 будем получать различные значения. Максимальные величины дает модуль вектора, а его направление по
будем получать различные значения. Максимальные величины дает модуль вектора, а его направление по 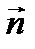 , когда максимально.Этот вектор называется ротором
, когда максимально.Этот вектор называется ротором  .
. 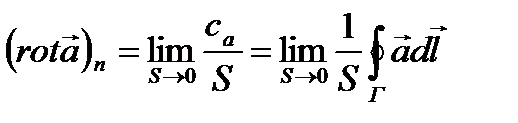 ;;
;; 
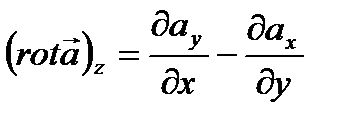

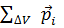 . Степень поляризации характеризуется вектором поляризации
. Степень поляризации характеризуется вектором поляризации  =
= 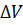 , т.е. дипольным моментом единицы объёма диэлектрика. Выполняется соотношение
, т.е. дипольным моментом единицы объёма диэлектрика. Выполняется соотношение 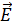 , где χ – диэлектрическая восприимчивость. РИСУНОК
, где χ – диэлектрическая восприимчивость. РИСУНОК
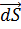 РИСУНОК
РИСУНОК и образующей l, пересекут выделенный участок
и образующей l, пересекут выделенный участок  à в объёме V, огранич. S, в результате поляризации возник связанный заряд q’=-
à в объёме V, огранич. S, в результате поляризации возник связанный заряд q’=- 
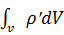 В силу произвольности S следует положить, что подынтегральное выражение (набла,
В силу произвольности S следует положить, что подынтегральное выражение (набла, 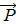 = ε0* χ *
= ε0* χ *  )=(набла, ε0* χ *
)=(набла, ε0* χ * 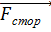 =q*
=q*  . Количественной характеристикой их является совершаемая ими работа на некотором участке цепи, отнесённая к величине переносимого заряда – ЭДС
. Количественной характеристикой их является совершаемая ими работа на некотором участке цепи, отнесённая к величине переносимого заряда – ЭДС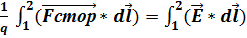
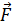 =q*
=q* 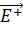 . Она характ. падением напряжения U12=
. Она характ. падением напряжения U12= 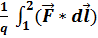 =
= 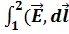 )+
)+ 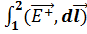 . Итак, U12=φ1-φ2+ε12. Для замкнутой цепи U=ε. Для однородных металлич. проводников в отсутствие магн.поля выполняется Закон Ома I=U/R=G*U. Если проводник цилиндрический, то R=ρ*l/S, σ=1/ρ- удельная проводимость. Выделим в проводнике цилиндр объём dl*dS_|_, образующие которого ||
. Итак, U12=φ1-φ2+ε12. Для замкнутой цепи U=ε. Для однородных металлич. проводников в отсутствие магн.поля выполняется Закон Ома I=U/R=G*U. Если проводник цилиндрический, то R=ρ*l/S, σ=1/ρ- удельная проводимость. Выделим в проводнике цилиндр объём dl*dS_|_, образующие которого ||  . РИСУНОК
. РИСУНОК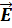 – закон Ома в дифф.форме.
– закон Ома в дифф.форме.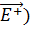 |*dl скалярно, j=I/S_|_ | à
|*dl скалярно, j=I/S_|_ | à 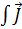 =
= 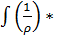 (
(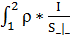 dl =
dl = 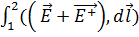 à I*R=U12= φ1-φ2+ ε12 – закон Ома для неоднородного участка цепи. Для замкнутой цепи I*R= ε, φ1=φ2.
à I*R=U12= φ1-φ2+ ε12 – закон Ома для неоднородного участка цепи. Для замкнутой цепи I*R= ε, φ1=φ2.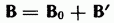
 .
.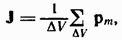
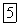 не имеет источников. Поэтому дивергенция результирующего поля (51.1) равна нулю:
не имеет источников. Поэтому дивергенция результирующего поля (51.1) равна нулю: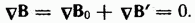
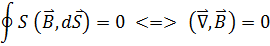
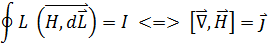

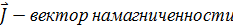
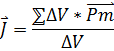

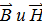 изменяются скачкообразно.
изменяются скачкообразно.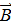 :
:

 испытывает скачок.
испытывает скачок.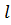 :
: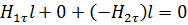
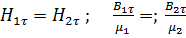

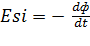 Её возникновение нельзя объяснить силами Лоренса, действ. на носители тока. Эти силы в среднем = 0, т.к. носители совершенно хаотично движутся.
Её возникновение нельзя объяснить силами Лоренса, действ. на носители тока. Эти силы в среднем = 0, т.к. носители совершенно хаотично движутся.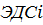 можно предположить, что изменяющееся со временем магн. поле порождает электр. поле. Действительно, как и любая ЭДС,
можно предположить, что изменяющееся со временем магн. поле порождает электр. поле. Действительно, как и любая ЭДС, 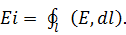 В соответствии с законом
В соответствии с законом 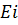 :
: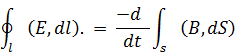
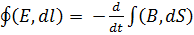 – это уравнение отображает закон электромагн. Индукции.
– это уравнение отображает закон электромагн. Индукции.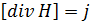
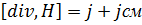
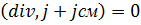 . Следовательно
. Следовательно 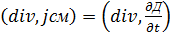
 эта величина явл. Характер. Скорости изменения со временем электр. поля
эта величина явл. Характер. Скорости изменения со временем электр. поля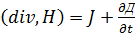 Видимо,что магн. поле может пораждаться не только движущими зарядами,но и изменяющимся со временем электр. поле даже в случае отсутствия заряда.
Видимо,что магн. поле может пораждаться не только движущими зарядами,но и изменяющимся со временем электр. поле даже в случае отсутствия заряда.

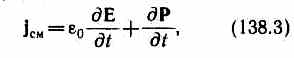 где e0 д E / д t — плотность тока смещения
где e0 д E / д t — плотность тока смещения первое уравнение связывает значение Е с изменениями вектора В во времени и является по существу выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов. Вторая пара уравнений
первое уравнение связывает значение Е с изменениями вектора В во времени и является по существу выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов. Вторая пара уравнений 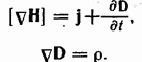 первое устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. Уравнения максвелла в скалярной форме
первое устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. Уравнения максвелла в скалярной форме 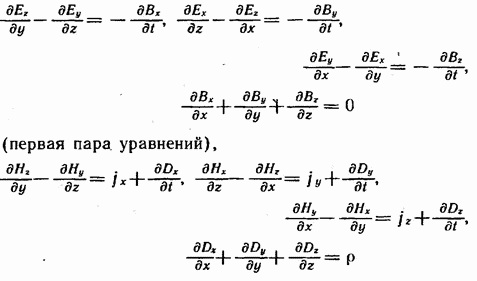
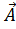 *cos(w*t-
*cos(w*t-  *
* 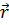 +α); V(скорость)=1/√(ε0*μ0* ε*μ)=c/√(ε*μ)=c/n
+α); V(скорость)=1/√(ε0*μ0* ε*μ)=c/√(ε*μ)=c/n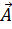 =
= 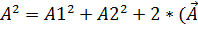 1,
1,  . Интенсивность волны прямопропорциональна квадрату амплитуды волныà
. Интенсивность волны прямопропорциональна квадрату амплитуды волныà 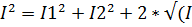 1*
1* 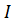 2)*cosδ
2)*cosδ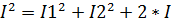 1*
1* 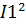 (1+ cosδ)=4*I1*(cos2δ)/2
(1+ cosδ)=4*I1*(cos2δ)/2 . Интенсивность результирующего колебания, зависящая от ∆, I(δ)=k*
. Интенсивность результирующего колебания, зависящая от ∆, I(δ)=k* 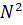
 Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути диск диаметром d. Диск закрывает первые m зон Френеля. Амплитуда колебания в точке Р равна A=A(m+1)/2
Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути диск диаметром d. Диск закрывает первые m зон Френеля. Амплитуда колебания в точке Р равна A=A(m+1)/2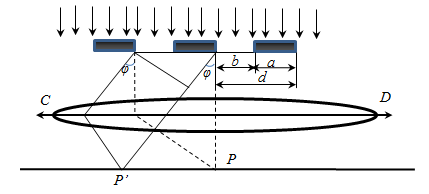 Дифракционная решетка представляет собой совокупность большого числа N одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине:
Дифракционная решетка представляет собой совокупность большого числа N одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине: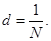
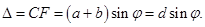 (1)
(1)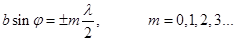
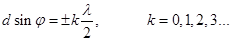 (3)
(3)


