Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция. Дифракция Френеля.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифракция - явление, которое можно рассматривать как отклонение от законов геометрической оптики при распространении волн. Первоначально понятие дифракции относилось только к огибанию волнами препятствий, но в современном, более широком толковании, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн в неоднородных средах, а также при распространении ограниченных в пространстве волн. Дифракция тесно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как частный случай интерференции (интерференция вторичных волн). Дифракция волн наблюдается независимо от их природы и может проявляться: в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении; в разложении волн по их частотному спектру; в преобразовании поляризации волн; в изменении фазовой структуры волн. Дифракция Френел я (дифракция в сходящихся лучах) – это дифракция, осуществляемая в случае, когда на препятствие падает сферическая волна, а дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути препятствие с круглым отверстием. Дифракционная картина наблюдается на экране, параллельном плоскости отверстия и находящемся от него на расстоянии b. Амплитуда света в точке P экрана будет равна A=A1/2 (+-) A(m)/2
Дифракция на диске.
В точке Р в центре геометрической тени всегда наблюдается интерференционный максимум, называемый пятном Пуассона, соответствующий половине действия только первой (m + 1) открытой зоны Френеля, и окруженный концентрическими с ним темными и светлыми кольцами. Дифракция Фраунгофера. Дифракция на щели Дифракция Фраунгофера (или дифракция плоских световых волн, или дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию.
Дифракция на одной щели. Пусть плоская монохроматическая волна с длиной волны лямбда нормально падает на очень длинную щель шириной b(длина щели l >>b). Плоскость щели и экран Э параллельны. Вследствие дифракции на узкой щели на экране наблюдается система интерференционных максимумов – размытых изображений источника света, разделенных темными промежутками интерференционных минимумов. Оптическая разность хода между волнами, исходящими от крайних точек щели равна треугольник=b*sin(фи) Результат интерференции света в точке Р (побочный фокус) определяется тем, сколько зон Френеля укладывается в щели. 1) если число m зон Френеля четное, то условие дифракционного минимума (полная темнота) имеет вид b*sin(фи)=(+-)m*лямбда 39. 2) если число m зон Френеля нечетное, то условие дифракционного максимума, соответствующего действию одной некомпенсированной зоны Френеля, записывается так: b*sin(фи)=(+-)(2*m+1)*лямбда/2
Дифракционная решетка
b - ширина щели; а - ширина непрозрачного участка; d = a + b - период решетки.
Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция. Т.к. щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки.
В направлениях, в которых наблюдается минимум для одной щели, будут минимумы и в случае N щелей, т.е. условие главных минимумов дифракционной решетки будет аналогично условию минимумов для щели:
40. (2) - условие главных минимумов. Условие максимумов; те случаи φ, которые удовлетворяют максимумам для одной щели, могут быть либо максимумами, либо минимумами, т.к. всё зависит от разности хода между лучами. Условие главных максимумов:
Эти максимумы будут расположены симметрично относительно центрального (нулевого k = 0) максимума. Для тех углов φ, для которых одновременно выполняется (2) и (3) максимума не будет, а будет минимум (например, при d =2b для всех четных k =2 р, р = 1, 2, 3...). Между главными максимумами имеются дополнительные очень слабые максимумы, интенсивность которых во много раз меньше интенсивности главных максимумов (1/22 интенсивности ближайшего главного максимума). Дополнительных максимумов будет N - 2, где N - число штрихов. Условие дополнительных максимумов:
Между главными максимума будут располагаться (N- 1) дополнительных минимумов. Условие дополнительных минимумов:
Таким образом, дифракционная картина, при дифракции на дифракционной решетке зависит от N и от отношения d/b. Пусть N =5, d/b =4. Тогда число главных максимумов(sin φ =1) k max < d/λ. Между ними по N -2 = 3 дополнительных максимума и N – 1 = 4 дополнительных минимума. При k / m = d/b =2,4,8... - главных максимумов не будет, а будут главные минимумы.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.007 с.) |

 знак «плюс» берется для случая, когда отверстие открывает нечетное число m зон Френеля, а знак «минус» – для четного m. Дифракционная картина будет иметь вид чередующихся темных и светлых колец с центром в точке Р.
знак «плюс» берется для случая, когда отверстие открывает нечетное число m зон Френеля, а знак «минус» – для четного m. Дифракционная картина будет иметь вид чередующихся темных и светлых колец с центром в точке Р. Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути диск диаметром d. Диск закрывает первые m зон Френеля. Амплитуда колебания в точке Р равна A=A(m+1)/2
Сферическая волна, распространяющаяся из точечного источника, встречает на своем пути диск диаметром d. Диск закрывает первые m зон Френеля. Амплитуда колебания в точке Р равна A=A(m+1)/2 Для наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.
Для наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.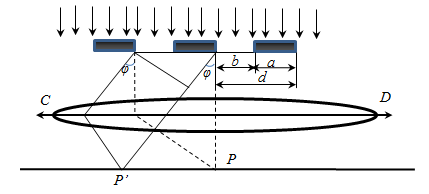 Дифракционная решетка представляет собой совокупность большого числа N одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине:
Дифракционная решетка представляет собой совокупность большого числа N одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине: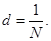
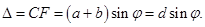 (1)
(1)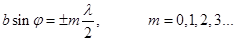
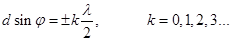 (3)
(3)