
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения дифракции света.Содержание книги
Поиск на нашем сайте
Лабораторная работа №7
Дифракция Фраунгофера. Цель работы: изучение дифракции Фраунгофера на одной щели и на дифракционной решетке.
Интерференция многих волн (многолучевая интерференция). Так как дифракция – это интерференция большого числа вторичных волн, рассмотрим многолучевую интерференцию.
В этом методе каждое колебание с амплитудой A 1 изображается вектором длиной A 1, а сдвиг фаз d между данным колебанием и другим изображается углом d между векторами, соответствующими данным колебаниям. Сумма этих векторов представляет собой вектор, соответствующий результирующему колебанию. На рисунке 4 показана векторная диаграмма сложения колебаний при интерференции N волн, возбуждающих в рассматриваемой точке P одинаково направленные когерентные колебания с амплитудами Из рисунка видно, что амплитуда результирующих колебаний равна:
Поэтому для амплитуды и интенсивности можно записать выражения:
где Главные максимумы интерференции N волн находятся в точках P, удовлетворяющих условию: При этом условии в формулах (4) возникает неопределенность 0/0. Однако, на основании правила Лопиталя можно показать, что отношение синусов в данных формулах в этом случае равно N. Поэтому амплитуда и интенсивность колебаний в главных максимумах:
Характер зависимости I/I1 от
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ Лабораторная установка
Рис.10. Установка для определения λ, d и диаметра мелких частиц.1–лазер, 2–экран, 3– столик для исследуемых предметов, 4–исследуемый предмет, 5–защитный экран, 6–блок питания, 7– рельс.
Расчеты по результатам измерений делаются на компьютере.
Определение длины волны лазерного излучения Для определения длины волны лазерного излучения установить решётку с периодом 1/500 мм между лазером и экраном 2 на расстояние В=120мм от экрана. Измерить на экране по линейке расстояние Аm от главного максимума до максимума второго порядка (m=2). При В=250мм измерить Аm от главного максимума до максимума первого порядка (m=1). Для вычисления длины волны используем формулу (14) λ = d/m • Sinφ (19) где φm ― угол дифракции m-го порядка
где В ― расстояние от решетки до экрана.
где ΔB, ΔA - ошибка определения B и Аm, равная 1/2 деления линеек.
Таблица1.
Определение периода решётки
Установить решетку с неизвестным периодом на расстоянии В1 = 75 см от экрана. Измерить расстояние А1 от главного максимума до максимума 1-го порядка. Затем установить решётку на расстояние B2 = 50 см и измерить расстояние A2 до максимума 2-го порядка. Для расстояния В3 = 25 см измерить А3 для максимума 3-го порядка. Рассчитать 3 значения периода решётки d по формуле:
Вычислить среднее значение периода. (λ и Δλ брать из предыдущих результатов)
Таблица2.
ПОДГОТОВКА ГОНИОМЕТРА К РАБОТЕ
Лабораторная работа №7
Дифракция Фраунгофера. Цель работы: изучение дифракции Фраунгофера на одной щели и на дифракционной решетке.
Основные положения дифракции света. Дифракцией света называется совокупность явлений, обусловленных волновой природой света и наблюдаемых при распространении света в средах с резкими неоднородностями (например: вблизи границ непрозрачных и прозрачных тел, сквозь малые отверстия). При прохождении световой волны в таких средах наблюдается отклонения от законов геометрической оптики, в частности, закона прямолинейного распространения света. В узком смысле, дифракция представляет собой огибание световыми волнами препятствий и проникновение света в область геометрической тени. Необходимо отметить также, что при дифракции за препятствием возникает перераспределение светового потока. В результате на экране, помещенном за препятствием, возникает дифракционная картина в виде светлых и темных полос (т.е. в виде максимумов и минимумов интенсивности света). Так как дифракция обусловлена волновой природой света, то она наблюдается, если размеры препятствия, отверстия или неоднородности соразмерны с длиной волны. Проникновение света в область геометрической тени объясняет принцип Гюйгенса, согласно которому каждая точка, до которой доходит волна в момент времени t, служит центром излучения вторичных сферических волн, огибающая этих волн дает положение фронта волны в последующий момент времени t+Δt. (рис.1).
.На рис.1 показан способ построения лучей и фронта s(t+Δt) плоской (а) и сферической (б) волн в моент времени (t+Δt) по известному фронту s(t) в момент времени t.
Пусть на преграду с отверстием падает параллельный ей фронт волны (рис.2а).
По Гюйгенсу каждая точка, выделяемого отверстием фронта, служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими, а огибающая этих волн дает фронт волны, прошедшей через отверстие. Из рис.2а видно, что за отверстием волна проникает в область геометрической тени (границы этой области показаны пунктиром), огибая край преграды, т.е. нарушается закон прямолинейного распространения света. Однако принцип Гюйгенса не дает информации об интенсивности волн, распространяющихся в различных направлениях, и не объясняет перераспределение светового потока при дифракции. Френель вложил в этот принцип идею когерентности вторичных волн и идею об их интерференции, создав таким способом принцип Гюйгенса-Френеля. В соответствии с этим принципом за отверстием в одних точках пространства, (например на экране Э, расположенным за отверстием рис.2б) в результате интерференции вторичных волн интенсивность света (I) будет большой, в других малой, т.е. будет происходить перераспределение светового потока в пространстве. Таким образом, между интерференцией и дифракцией нет принципиального различия, так как дифракция света – это интерференция вторичных волн. Рассмотрим аналитическое выражение принципа Гюйгенса-Френеля. Каждый элемент (dS) волновой поверхности (S) служит источником вторичной сферической волны, амплитуда которой пропорциональна площади элемента dS и убывает с расстоянием r от источника по закону 1/r (рис.3). Каждая вторичная волна, идущая от каждого участка dS возбуждает в точке P, лежащей перед волновой поверхностью S, колебание:
Результирующее колебание в точке P представляет собой наложение (суперпозицию) колебаний (1), создаваемых всеми элементами dS, находящимися на поверхности S:
Эта формула является аналитическим выражением принципа Гюйгенса-Френеля и позволяет рассчитывать результирующую амплитуду и интенсивности света при дифракции. Различают два вида дифракции: дифракцию Фраунгофера и дифракцию Френеля. Дифракция Фраунгофера – это дифракция в параллельных лучах (или дифракция плоских волн). Она наблюдается, когда источник света и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи идущие в точку наблюдения, практически параллельны. Дифракция Фраунгофера может быть осуществлена при помещении источника в фокусе собирающей линзы, установленной перед препятствием, а дифракционная картина наблюдается в фокальной плоскости второй собирающей линзы, установленной за препятствием, или с помощью зрительной трубы, настроенной на бесконечность. При использовании в качестве источника света лазера, собирающая линза перед препятствием не требуется, так как лучи светового пучка лазера практически параллельны. Дифракция Френеля – это дифракция в сходящихся лучах. В этом случае на препятствие падает сферическая или плоская волна, а дифракционная картина наблюдается на экране, находящемся за препятствием на конечном расстоянии от него.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.12.88 (0.007 с.) |

 Для нахождения амплитуды A результирующих колебаний и интенсивности света (
Для нахождения амплитуды A результирующих колебаний и интенсивности света ( ) в произвольной точке P интерференционной картины воспользуемся методом векторных диаграмм для сложения одинаково направленных колебаний.
) в произвольной точке P интерференционной картины воспользуемся методом векторных диаграмм для сложения одинаково направленных колебаний. и не зависящим от i сдвигом фаз между (i+1)-м и i -м колебаниями
и не зависящим от i сдвигом фаз между (i+1)-м и i -м колебаниями  .
.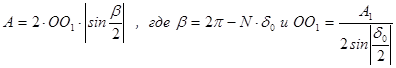 (3)
(3) (4)
(4) - интенсивность света в точке P, создаваемая каждой из N интерферирующих волн порознь.
- интенсивность света в точке P, создаваемая каждой из N интерферирующих волн порознь. , где m =0,1,2,… - порядок главного максимума.
, где m =0,1,2,… - порядок главного максимума.
 Интерференционные минимумы (A=0) удовлетворяют условию:
Интерференционные минимумы (A=0) удовлетворяют условию:  , где p принимает любые положительные значения, кроме кратных N. При этом условии в формулах (4) равен нулю только числитель (но не знаменатель).
, где p принимает любые положительные значения, кроме кратных N. При этом условии в формулах (4) равен нулю только числитель (но не знаменатель). показан на рис.5. Между каждой парой соседних интерференционных минимумов находится один максимум – либо главный, либо побочный. При больших N интенсивности побочных максимумов пренебрежимо малы по сравнению с интенсивностью главных максимумов. Двум минимумам, ограничивающим главный максимум n -го порядка, соответствуют значения
показан на рис.5. Между каждой парой соседних интерференционных минимумов находится один максимум – либо главный, либо побочный. При больших N интенсивности побочных максимумов пренебрежимо малы по сравнению с интенсивностью главных максимумов. Двум минимумам, ограничивающим главный максимум n -го порядка, соответствуют значения 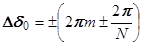 . Поэтому «ширина» главного максимума, равная 4p/N, обратно пропорциональна числу N интерферирующих волн, а его интенсивность пропорциональна N 2.
. Поэтому «ширина» главного максимума, равная 4p/N, обратно пропорциональна числу N интерферирующих волн, а его интенсивность пропорциональна N 2.
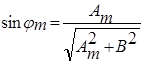
 (20)
(20)
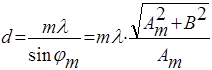 (21)
(21)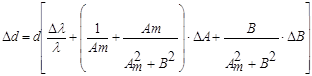


 (1)
(1) где
где  - амплитуда волны в точке P, (
- амплитуда волны в точке P, (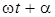 ) – фаза колебаний в месте расположения волновой поверхности S, k-волновое число,
) – фаза колебаний в месте расположения волновой поверхности S, k-волновое число,  - множитель, который определяется амплитудой колебания в том месте, где находится dS; r – расстояние от dS до точки P. Коэффициент
- множитель, который определяется амплитудой колебания в том месте, где находится dS; r – расстояние от dS до точки P. Коэффициент  зависит от угла j между нормалью
зависит от угла j между нормалью  к площадке dS и направлением от dS к точке P.
к площадке dS и направлением от dS к точке P.  (2)
(2)


