
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения пуассона и лапласаСодержание книги
Поиск на нашем сайте
Основными ур-иями эл/статики в вакууме являются (набла,Е)=ρ/ε0 и [набла,Е]=0. Первое ур-ие позволяет по известному распределению заряда в пр-ве найти вектор Е. Второе ур-ие говорит о потенциальности эл/стат. поля, что позволяет выразить напряжённость через скалярную ф-цию φ: E=-φ*набла. Подставим это в первок ур-ие: (набла, набла*φ)=- ρ/ε0à потенциал удовлетворяет ур-ию набла^2* φ=- ρ/ε0, ∆φ=- ρ/ε0 – ур-ие Пуассона, оператор Лапласса ∆=∂^2/∂x^2+∂^2/∂y^2+∂^2/∂z^2. В отсутствии зарядов ρ=0 ур-ие переходит в ур-ие Лапласса ∆φ=0. Решая задачи электростатики, можно находить векторную ф-цию вектора Е с помощью дифф. ур-ия первого порядка либо искать скалярную ф-цию φ, используя ур-ие Пуассона второго порядка. Рассмотрим бесконечный круглый цилиндр радиуса r, заряженный равномерно с зарядом плотностью ρ РИСУНОК Найдём потенциал поля, используя ур-ие Пуасона. Потенциал будет зависеть только от расстояния точки наблюдения φ(r), где r=√(x^2+y^2) ∂^2*φ/∂x^2+∂^2*φ/∂y^2=- ρ/ε0; ∂φ/∂x=∂φ/∂r * ½ * 2x/r = x/r * ∂φ/∂r ∂^2*φ/∂x^2=1/r * ∂φ/∂r + x(-1)*2x/(2r^3)* ∂φ/∂r + x^2/r^2 * ∂^2*φ/∂r^2. Аналогично для у Сложив вторые производные, получаем: ∂^2*φ/∂x^2+∂^2*φ/∂y^2 = 2/r * ∂φ/∂r – 1/r * ∂φ/∂r + ∂^2*φ/∂r^2 = 1/r *d/dr * (r* ∂φ/∂r). Ур-ие Пуассона внутри цилиндра 1)r<R: 1/r *d/dr * (r* ∂φ/∂r) =- ρ/ε0 * r à r* ∂φ/∂r= - ρ*r^2/(2*ε0)+A/r Φ=- ρ*r^2/(4*ε0)+A*lnr+B 2)r>R: 1/r *d/dr * (r* ∂φ/∂r)=0 à r* ∂φ/∂r=C или ∂φ/∂r=C/r à φ=C*lnr+D Потенциал определён с точностью до постоянного слагаемого, которое определяется выбором его значения на некоторой эквипотенциальной пов-сти. Положим, что на оси цилиндра φ=0 à A=0, B=0 à φ внутри = - ρ*r^2/(4*ε0) Потенциал удовлетворяет ур-ию второго порядка à он должен быть, как и его первая производная, непрерывной функцией. Условие непрерывности потенциала и его первой производной нужно записать при r=R: φ внутри = - ρ*r^2/(4*ε0); - ρ*r^2/(4*ε0)= C*lnr+D и С=- ρ*R^2/(2*ε0); D=- ρ*r^2/(4*ε0)+ ρ*R^2/(2*ε0) * lnR
Электрическое поле в диэлектриках. Объемные и поверхностные связанные заряды. Эл.заряды размещены на телах. Тела бывают диэлектриками, полупроводниками и проводниками.
Диэлектрики – вещества, не способные проводить эл.ток вследствие отсутствия в диэлектриках свободных зарядов. Свободные заряды – это заряды, способные под воздействием сколь угодно малой силы перемещаться по всему объёму тела. Диэлектрики подразделяют на неполярные, полярные и диэлектрические ионные кристаллы. Диполярные диэлектрики состоят из симметричных молекул(Н2, О2), т.к. центры тяжести полож. и отриц. зарядов в среднем совпадают при помещении такой молекулы в электр.поле. Её полож. заряды смещаются по полю, отриц. – против поля. В результате молекула приобретает дипольный момент В широких пределах изменения фих.величин выполняется Поляризуемость молекулы. В результате любой объём V диэлектрика приобретает дипольный момент. В результате поляризации диэлектрика на его поверхности и по объёму возникают заряды Отличают сторонние и связанные заряды. Обозначают q(ст) и q’(связ). Сторонние заряды – это заряды, которые мы можем заряжать и перемещать. Связанные – это заряды, возникшие в результате смещения зарядов диэлектрика в пределах своих молекул. Связанные заряды наряду со сторонними создают эл.поле. В результате мы наблюдаем Выберем в изотопном диэлектрике некоторую поверхность S и вычислим заряд q’, прошедший через эту пов-сть, при включении внешнего эл.поля. Выделяем площадку Очевидно, что все положительные заряды, находящиеся в пределах цилиндра с основанием Заряд, прошедший через dS в направлении нормали, в результате поляризации dq’=( Пусть S – замкнутая пов-сть. Тогда из объёма, ограниченного этой пов-стью, вышел q св q’ выш. =
Вблизи пов-сти, вблизи границы диэлектрика выделим dS*dh РИСУНОК Появился заряд dq’=( Несимметричные молекулы NH, HCl, CO изначально обладают дипольным моментом Диэлектрические ионные кристаллы состоят из двух подрешёток: положительной и отрицательной, которые сдвигаются при включении внешнего поля. В результате возникает ненулевой вектор Выясним, когда в диэлектрике возникают объёмные связанные заряды: поле создаётся как сторонними, так и связанными зарядами, поэтому для E следует записать т.Гаусса (набла,Е)=(ρ+ρ’)/ε0; (набла, Ненулевая объёмная ρ связ.зарядов возникает в поляр. диэлектрике,если: 1)диэлектрик не однороден, т.е. (набла, χ) не равно 0 2)по V диэлектрика распределён сторонний заряд
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.008 с.) |

 =e*l, l=l1+l2. РИСУНОК
=e*l, l=l1+l2. РИСУНОК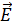
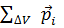 . Степень поляризации характеризуется вектором поляризации
. Степень поляризации характеризуется вектором поляризации  =
= 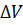 , т.е. дипольным моментом единицы объёма диэлектрика. Выполняется соотношение
, т.е. дипольным моментом единицы объёма диэлектрика. Выполняется соотношение 
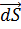 РИСУНОК
РИСУНОК и образующей l, пересекут выделенный участок
и образующей l, пересекут выделенный участок  à в объёме V, огранич. S, в результате поляризации возник связанный заряд q’=-
à в объёме V, огранич. S, в результате поляризации возник связанный заряд q’=- 
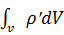 В силу произвольности S следует положить, что подынтегральное выражение (набла,
В силу произвольности S следует положить, что подынтегральное выражение (набла, 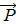 = ε0* χ *
= ε0* χ *  )=(набла, ε0* χ *
)=(набла, ε0* χ * 


