Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индукционный ток направлен так, чтобы противодействовать изменению магнитного потока.Содержание книги
Поиск на нашем сайте
Учет знака “—”позволяет определить направление ЭДС индукции, если нормаль к охватываемой поверхности и направлению обхода контура образуют правовинтовую систему. Изменение потока может быть вызвано ( В качестве замкнутого контура выбираем П-образный проводник, который замкнут проводящим тонким стержнем длины Пусть стержень движется со скоростью V. На плоскости тела действует сила F=q*[V,B]. Она действует только в пределах стержня. Это сторонняя сила. Она характеризуется Ei РИСУНОК Ei= Итак, Ei=-(B, n*dS)/dt = -dФ/dt
Следует отметить, что под действием сторонних сил, носители тока начинают двигаться вдоль проводника со скоростью Работа силы Лоренца Работа сторонних сил совершается засчет действия внешней силы, уравновешивающей силы Лоренца. 28.Энергия магнитного поля В соответствии с законом Био—Савара магнитная индукция В пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток 1 в контуре и создаваемый им полный магнитный поток
Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура.
При изменениях силы тока в контуре возникает э. д. с. самоиндукции
Если при изменениях силы тока индуктивность остается постоянной (что возможно лишь при отсутствии ферромагнетиков), выражение для э.д.с. самоиндукции имеет вид
Рис. 67.1. возникающей в соленоиде э. д. с. самоиндукции. Работа, совершаемая этим током за время dt равна
Если индуктивность соленоида не зависит от I(L=const), то
Проинтегрировав это выражение по I в пределах от первоначального значения I до нуля, получим работу, совершаемую в цепи за все время, в течение которого происходит исчезновение магнитного поля,
Работа (67.3) идет на приращение внутренней энергии сопротивления R, соленоида и соединительных проводов (т. е. на их нагревание). Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем соленоид пространстве. Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа (67.3). Таким образом, мы приходим к выводу, что проводник с индуктивностью L, по которому течет ток силы I, обладает энергией
которая локализована в возбуждаемом током магнитном поле (ср. эту формулу с выражением
Выражение (67.3) можно трактовать как работу, которую необходимо совершить против э.д.с. самоиндукции в процессе нарастания тока от 0 до I и которая идет на создание магнитного поля, обладающего энергией (67.4). Действительно, работа, совершаемая против э.д.с. самоиндукции, равиа
Проделав преобразования, подобные тем, которые привели нас к выражению (67.2), получим
что совпадает с (67.3). Работа (67.5) совершается при установлении тока за счет источника э. д. с. и идет целиком на создание магнитного поля, сцепленного с витками соленоида. Выражение (67.5) не учитывает той работы, которую источник э. д. с. затрачивает в процессе установления тока на нагревание проводников. Выразим энергию магнитного поля (67.4) через величины, характеризующие само поле. В случае очень длинного (практически бесконечного) соленоида
(см. формулы (64.3) и (53.8)). Подставив эти значения L и I в выражение (67.4) и произведя преобразования, получим
Магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида. Следовательно, энергия (67.6) локализована внутри соленоида и распределена по его объему с постоянной плотностью w, которую можно найти, разделив W на V. Произведя это деление, получим
Воспользовавшись соотношением (52.14), формуле для плотности энергии магнитного поля можно придать вид
Полученные нами выражения для плотности энергии магнитного поля отличаются от выражений (30.3) для плотности энергии электрического поля лишь тем, что электрические величины в ни заменены соответствующими магнитными. Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенную в любом объеме V. Для этого нужно вычислить интеграл
Можно показать, что в случае связанных контуров (в отсутствие ферромагнетиков) энергия поля определяется формулой
Для энергии N связанных друг с другом контуров получается аналогичное выражение
где
Вихревое электрическое поле Магнитный поток через поверхность ограниченную замкн. проводящим контуром, может изменяться за счёт изменения индукции магнитного поля В при неподвижном конуре. В этом случае также возник. ЭДС индукции Для объяснения возник. Максвелл предположил, что E возникает во всём пространстве при изменении B и не зависит от наличия замкнутого проводящего контура. Контур служит для обнаружения возникшего электр. поля. Поэтому контур L выбирается как воображаемый контур. Для выполнения последнего равенства следует положить [набла,Е]=-∂B/∂t В отличие от электростатики, когда заряды неподвижны, электр. поле может быть вихревым, не потенциальным. В интегральной форме эквивалентное уравнение имеет вид:
Ток смещения Одним из основных уравнений магнитостатики явл. Максвелл предположил,что уравнение для напряжённости магн. поля H следует писать в виде Должно выполн. Таким образом плотность тока смещения С учётом плотности тока смещения т. О циркуляции для H в диф. Формуле запишется Ток смещения Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
Выражение (138.2) и было названо Максвеллом плотностью тока смещения. Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле В диэлектриках ток смещения состоит из двух слагаемых. Так как, согласно (89.2), D =e0 E + P, где Е — напряженность электростатического поля, а Р — поляризованность (см. § 88), то плотность тока смещения
в вакууме, д P / д t — плотность тока поляризации — тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах). Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по своей природе не отличаются от токов проводимости. Однако то, что и другая (e0 д E / д t), часть плотности тока смещения (e0 д E / д t), не связанная с движением зарядов, а обусловленная только изменением электрического поля во времени, также возбуждает магнитное поле, является принципиально новым утверждением Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возникновению в окружающем пространстве магнитного поля.
УРАВНЕНИЕ МАКСВЕЛЛА Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Основу электромагнитной теории света максвелла образуют уравнения максвелла. Первая пара уравнений максвелла
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 ) изменением размеров и формы контура, его движением и поворотами, а также в результате изменения магнитного поля.
) изменением размеров и формы контура, его движением и поворотами, а также в результате изменения магнитного поля. , где В перпендик. плоскости контура.
, где В перпендик. плоскости контура. /q =
/q =  =([V,B],l)=(B,[l,dr/dt]); [l,dr]=-dS*n
=([V,B],l)=(B,[l,dr/dt]); [l,dr]=-dS*n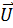 . След-но, их скорость
. След-но, их скорость  . За dt они совершают перемещение
. За dt они совершают перемещение  .
. =0
=0 . При изменениях I изменяется также и
. При изменениях I изменяется также и 
 равная
равная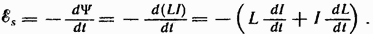

 Рассмотрим цепь, изображенную на рис. 67.1. При замкнутом ключе в соленоиде установится ток I, который обусловит магнитное поле, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление R будет некоторое время течь постепенно убывающий ток, поддерживаемый
Рассмотрим цепь, изображенную на рис. 67.1. При замкнутом ключе в соленоиде установится ток I, который обусловит магнитное поле, сцепленное с витками соленоида. Если разомкнуть ключ, то через сопротивление R будет некоторое время течь постепенно убывающий ток, поддерживаемый (67.1)
(67.1) и выражение (67.1) принимает вид
и выражение (67.1) принимает вид (67.2)
(67.2) (67.3)
(67.3) (67.4)
(67.4)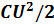 для энергии заряженного конденсатора.
для энергии заряженного конденсатора.
 (67.5)
(67.5)
 (67.6)
(67.6) (67.7)
(67.7) (67.8)
(67.8) (67.9)
(67.9) (67.10)
(67.10) (67.11)
(67.11) =
=  - взаимная индуктивность i-го и k-го контуров, а — индуктивность
- взаимная индуктивность i-го и k-го контуров, а — индуктивность  =
=  контура.
контура.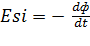 Её возникновение нельзя объяснить силами Лоренса, действ. на носители тока. Эти силы в среднем = 0, т.к. носители совершенно хаотично движутся.
Её возникновение нельзя объяснить силами Лоренса, действ. на носители тока. Эти силы в среднем = 0, т.к. носители совершенно хаотично движутся.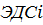 можно предположить, что изменяющееся со временем магн. поле порождает электр. поле. Действительно, как и любая ЭДС,
можно предположить, что изменяющееся со временем магн. поле порождает электр. поле. Действительно, как и любая ЭДС, 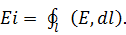 В соответствии с законом
В соответствии с законом 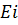 :
: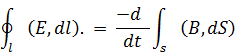
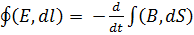 – это уравнение отображает закон электромагн. Индукции.
– это уравнение отображает закон электромагн. Индукции.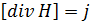
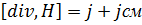
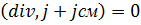 . Следовательно
. Следовательно 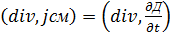
 эта величина явл. Характер. Скорости изменения со временем электр. поля
эта величина явл. Характер. Скорости изменения со временем электр. поля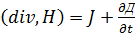 Видимо,что магн. поле может пораждаться не только движущими зарядами,но и изменяющимся со временем электр. поле даже в случае отсутствия заряда.
Видимо,что магн. поле может пораждаться не только движущими зарядами,но и изменяющимся со временем электр. поле даже в случае отсутствия заряда.

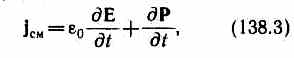 где e0 д E / д t — плотность тока смещения
где e0 д E / д t — плотность тока смещения первое уравнение связывает значение Е с изменениями вектора В во времени и является по существу выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов. Вторая пара уравнений
первое уравнение связывает значение Е с изменениями вектора В во времени и является по существу выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов. Вторая пара уравнений 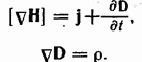 первое устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. Уравнения максвелла в скалярной форме
первое устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. Уравнения максвелла в скалярной форме