
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновое уравнение для электромагнитного поляСодержание книги
Поиск на нашем сайте
Существование электромагнитных волн вытекает из уравнений максвелла. В случае однородной нейтральной непроводящей среды с постоянными проницаемостями µ и ɛ
Поэтому уравнения максвелла можно записать следующим образом
ПЛОСКАЯ ЭЛЕКТРОМАГНИТНАЯ ВОЛНА Волна называется плоской, если поверхности равных фаз представляют собой плоскость, т.е. в плоской электромагнитной волне векторы Однородной плоской волной называется волна, в которой при соответствующем выборе осей координат векторы Если векторы По определению плоской волны В плоской волне Решение линейного дифференциального уравнения второго порядка имеет вид
Энергия и импульс электромагнитной волны. ЭМ волна обладает энергией, которая в результате волнового процесса переносится в пространстве. Энергия ЭМ волны это энергия эл и магн полей. Для плотности энергии
E и H меняются со временем => плотность энергии в выбр точке будет меняться от wmin=0 до Вектор плотности потока энергии
Полученный вектор называют вектором Поинтинга. Зная вектор поинтинга можно вычислить поток энергии через произвольную поверхность.
При прохождении эм волны через некоторое тело, она оказывает на него силовое воздействие: вектор E заставляет электроны проводимости двигаться, возникает эл ток, плотность которого сигмаE, действует сила Лоренца, которая и есть воздействие на тело, эта сила вызывает изменение импульса тела => волна обладает импульсом.
Интерференция световых волн Световые волны представляют собой часть спектра э/м волн. Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями эл.вектора Е. Поэтому вектор Е называют световым вектором. Его поведение даётся выражением Среда с большим значением n называется более оптически плотной. Видимому диапазону света соответствуют длины волн λ=0.4-0.76 мкм; V=c/ λ0 Пусть 2 волны одной частоты, накладываясь друг на друга, возбуждают колебания. Согласно принципу суперпозиции, мы наблюдаем колебания
В случае сложения когерентных волн интенсивность не равна сумме интенсивностей волн, а будет меняться при переходе от одной т. пространства в другую, т.к. -1<= cosδ<=1. Это явление называют интерференцией. Происходит распределение интенсивности света в пространстве; в результате возникают чередующиеся max и min интенсивности. Естественные источники света некогерентны, поэтому для наблюдения интерференции поступают след.образом: С помощью отражений и преломлений пучок света разбивают на 2 пучка,которые проходят различные пути s1, s2 в средах с показателем преломления n1, n2, а затем сводят их вместе РИСУНОК Если закон A*cos(w*t), то в т.Р приходят колебания A1*cos(w*(t-s1/v1)) и A2*cos(w*(t-s2/v2)). S=w*s1/v1-w*s2/v2=(w/c)*(n1*s1-n2*s2)=(2*π/λ0)*(n1*s1-n2*s2) Разность фаз определяется оптической разностью хода ∆= n1*s1-n2*s2; δ=(2*π/λ0)* ∆ Максимумы интенсивности будет наблюдаться при условии δ=+-2*π*m; ∆=+-m* λ0=+-2*m* λ0/2 Минимумы интенсивности наблюдаются при δ=+-(2*m+1)*π или ∆=+-(2*m+1)* λ0/2 Интерференцию в лаб.условиях наблюдал Юнг. Слабый пучок света падал на экран с двумя близко расположенными отверстиями, интерференция наблюдалась на другом параллельном экране РИСУНОК Тогда разность хода ∆ =s2-s1=d*sinθ=d*tgθ=d*x/l Оптическая разность тока ∆=n*dx/làусловие наблюдения максимумов на экране будет n*dxmax/l=+-m* λ0 и минимумов n*dxmin/l=+-(m+0.5)* λ0. Видно, что расстояние между соседними максимумами одинаково ∆х=l/d * λ0/n=l* λ/d. На экране max и min равномерно чередуются. При естественном предположении равенства интенсивности двух лучей для результирующей интенсивности получаем:
Max интенсивности в 4 раза больше интенсивности одного луча. Зная геометрию установки, по измеренному dx можно определить длину волны падающего света
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |


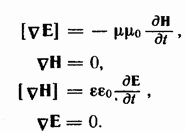 Из этих уравнений можно составить уравнение
Из этих уравнений можно составить уравнение  Взяв ротор от обейх частей этого уравнения придем к уравнению
Взяв ротор от обейх частей этого уравнения придем к уравнению  уравнения получены из первого и третьего уравнений максвелла. Составленные уравнения представляют собой типичные волновые уравнения. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну. Они указывают на то, что электромагнитные поля могу сущетсвовать в виде электромагнитных волн, фазовая скорость которых равна
уравнения получены из первого и третьего уравнений максвелла. Составленные уравнения представляют собой типичные волновые уравнения. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну. Они указывают на то, что электромагнитные поля могу сущетсвовать в виде электромагнитных волн, фазовая скорость которых равна 
 и
и  расположены в плоскости хода, перпендикулярно направлению распространения волны.
расположены в плоскости хода, перпендикулярно направлению распространения волны.
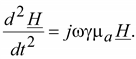

 , где H – напряжённость магнитного поля.
, где H – напряжённость магнитного поля.
 , где V – скорость волны.
, где V – скорость волны. . Таким образом энергия распространяется в пространстве. Для кол-венной хар-ки направления и интенсивности используется вектор плотности потока энергии, который направлен в сторону распространения волны. Его модуль равен энергии, переносимой в ед времени, через ед. площадку перпендикулярную
. Таким образом энергия распространяется в пространстве. Для кол-венной хар-ки направления и интенсивности используется вектор плотности потока энергии, который направлен в сторону распространения волны. Его модуль равен энергии, переносимой в ед времени, через ед. площадку перпендикулярную 
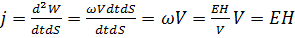

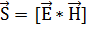
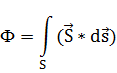
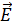 =
= 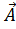 *cos(w*t-
*cos(w*t-  *
* 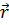 +α); V(скорость)=1/√(ε0*μ0* ε*μ)=c/√(ε*μ)=c/n
+α); V(скорость)=1/√(ε0*μ0* ε*μ)=c/√(ε*μ)=c/n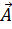 =
= 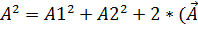 1,
1,  . Интенсивность волны прямопропорциональна квадрату амплитуды волныà
. Интенсивность волны прямопропорциональна квадрату амплитуды волныà 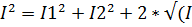 1*
1* 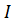 2)*cosδ
2)*cosδ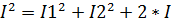 1*
1* 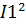 (1+ cosδ)=4*I1*(cos2δ)/2
(1+ cosδ)=4*I1*(cos2δ)/2


