
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контур с током в однородном магнитном полеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим контур с постоянным током I, находящийся в однородном магнитном поле. На каждый элементарный участок контура действует сила Ампера Сила, действующая на контур в целом, равна сумме сил, действующих на все элементарные участки контура, и может быть выражена как
Учитывая, что I = const и в однородном магнитном поле В =
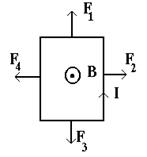
Векторный интеграл Но это не означает, что равны нулю силы, действующие на отдельные участки контура. Например, на прямоугольный контур, плоскость которого перпендикулярна силовым линиям однородного магнитного поля, действуют растягивающие или сжимающие его силы (см. рисунок).
В этом случае на стороны b действуют силы, которые деформируют контур, но не вызывают его движения.
Модули этих сил равны F a = IaB. Силы М = F a b sina = IabB sina = IBS sina, где S – площадь контура; a – угол между вектором F a и продолжением стороны b контура; этот угол равен по величине углу между единичным вектором n и вектором В. В векторной форме данное выражение имеет вид
где n – единичный вектор, направленный по положительной нормали к контуру. Выражение для момента сил можно записать и в такой форме: M = [ pm, B ] , где pm = IS n – магнитный момент контура с током; направление магнитного момента совпадает с положительной нормалью к контуру. Из выражения для расчёта M следует, что величина момента сил зависит от ориентации контура в магнитном поле. Момент сил, действующий на контур максимален, если контур параллелен силовым линиям магнитного поля (при этом угол между магнитным моментом и вектором магнитной индукции равен 900). Если же контур перпендикулярен им, то момент сил равен нулю. Поэтому если магнитный момент pm контура с током параллелен вектору В, то в однородном магнитном поле контур будет находиться в состоянии устойчивого равновесия. Контур будет в равновесии и в том случае, когда a = 1800, но равновесие будет неустойчивым. Следует отметить, что все выводы, сформулированные в данном разделе, верны и для контура произвольной формы, находящегося в однородном магнитном поле.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.226 (0.008 с.) |

 .
. .
.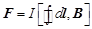 .
.
 . Поэтому результирующая сила, действующая на контур, равна нулю.
. Поэтому результирующая сила, действующая на контур, равна нулю. Повернём контур так, чтобы положительная нормаль к его плоскости образовала некоторый угол a с силовыми линиями (направление положительной нормали определяют по правилу правого винта).
Повернём контур так, чтобы положительная нормаль к его плоскости образовала некоторый угол a с силовыми линиями (направление положительной нормали определяют по правилу правого винта). Силы, действующие на стороны а контура, стремятся повернуть контур так, чтобы вектор n был параллелен вектору В (вектор n – единичный вектор, направление которого совпадает с положительной нормалью к контуру).
Силы, действующие на стороны а контура, стремятся повернуть контур так, чтобы вектор n был параллелен вектору В (вектор n – единичный вектор, направление которого совпадает с положительной нормалью к контуру). и
и  создают момент пары сил, модуль которого равен
создают момент пары сил, модуль которого равен .
.


