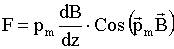Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циркуляция для плоского контура, охватывающего бесконечный прямой проводник с токомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ток за контуром
11.5.4. Формулировка теоремы о циркуляции
Например:
Ток I4 в сумму не входит! 11.5.5. Применение теоремы о циркуляции для вычисления магнитного поля бесконечно длинного соленоида
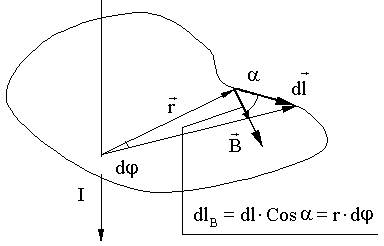
Выберем такой контур, как на рисунке, т.к. из соображений симметрии вектор
1) В интервалах от точки 2 до точки 3 и от точки 4 до точки 1
3) Можно показать, что вне бесконечного соленоида B=0, т.е.
Значит:
т.к. внутри соленоида B = Bl = const, то
По теореме о циркуляции (11.5.4)
Откуда магнитное поле бесконечного соленоида:
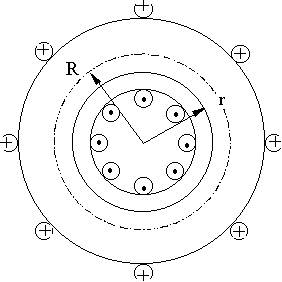
Направлено Магнитное поле тороида
Магнитное поле тороида:
Вне тора поле Закон Ампера
Сила Лоренца - это сила, действующая со стороны магнитного поля на движущийся в нем заряд
См. (10.2), (10.2.1) n-концентрация носителей. Сила Ампера (11.6) есть сумма сил Лоренца.
Направление силы Лоренца для положительного заряда совпадает с направлением векторного произведения
Движение заряженной частицы в однородном магнитном поле 11.7.1.1.
Линии индукции направлены за чертеж, В = const.
Из (3.10.1)
Частица движется по окружности такого радиуса:
11.7.1.2.
11.7.1.3. Угол между скоростью и магнитным полем
Движение - сумма движения (11.7.1.1) со скоростью Траектория - спираль. Радиус спирали:
Шаг спирали:
Рамка с током в магнитном поле Плоский контур в однородном поле
Магнитный момент контура - это вектор, модуль которого
Направление вектора Вектор вращающего момента
Плоский круговой контур в неоднородном осесимметричном магнитном поле 11.8.2.1.Магнитный момент против поля
Магнитный момент по полю
Контур разворачивается так, чтобы 11.8.2.3. Сила, действующая на контур при произвольной ориентации Эта сила направлена по оси симметрии поля z и равна:
11.9. Поток вектора магнитной индукции (магнитный поток) 11.9.1. Для однородного
11.9.2. Поток вектора
11.9.3. Поток вектора
11.10. Явление электромагнитной индукции состоит в том, что любое изменение магнитного потока Ф, пронизывающего замкнутый контур, вызывает появление индукционного тока в контуре.
Закон Фарадея - Ленца Закон Фарадея-Ленца утверждает, что ЭДС индукции равна скорости изменения магнитного потока, взятой с обратным знаком.
Знак минус напоминает о правиле Ленца: индукционный ток имеет такое направление, чтобы создаваемое им магнитное поле препятствовало изменению магнитного потока.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.97.1 (0.01 с.) |

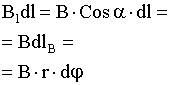 Из (11.4.1):
Из (11.4.1):

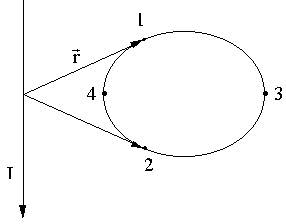
 поворачивается по часовой стрелке, от 2 к 1 через 4 - на тот же угол против часовой стрелки. В результате
поворачивается по часовой стрелке, от 2 к 1 через 4 - на тот же угол против часовой стрелки. В результате

 по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е.
по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е. .
.
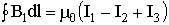

 .
. стороне контура, значит Вl = 0.
стороне контура, значит Вl = 0. .
. .
. ,
, .
. .
.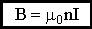 .
.
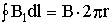 .
По теореме о циркуляции:
.
По теореме о циркуляции:
 ,
,  , R - радиус тора.
, R - радиус тора.
 .
.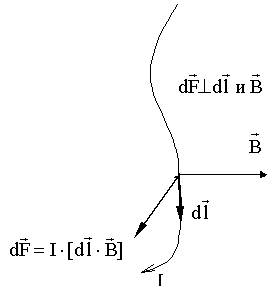
 проводника с током I, помещенного в магнитное поле, действует сила
проводника с током I, помещенного в магнитное поле, действует сила  , которая определяется следующим образом. Направлен вектор
, которая определяется следующим образом. Направлен вектор 
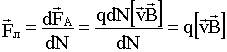
 .
.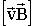 , для отрицательного - противоположно ему.
, для отрицательного - противоположно ему.
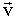 перпендикулярна
перпендикулярна 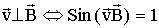 )
)
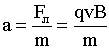 ,
, нормальное ускорение.
нормальное ускорение. .
.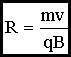 .
. 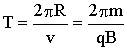 .
. ) = 0
) = 0
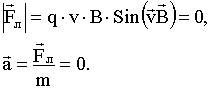
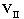 - направлена вдоль магнитного поля,
- направлена вдоль магнитного поля,  направлена перпендикулярно магнитному полю.
направлена перпендикулярно магнитному полю.
 .
.
 и движения (11.7.1.2) со скоростью
и движения (11.7.1.2) со скоростью  .
.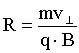
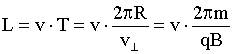

 .
. определяется правилом правого винта: винт перпендикулярен к контуру, и вращаем по току. Поступательное движение укажет направление.
определяется правилом правого винта: винт перпендикулярен к контуру, и вращаем по току. Поступательное движение укажет направление.
 При параллельности
При параллельности 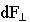 сжимают контур, а
сжимают контур, а 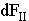 выталкивают его в область более слабого поля.
выталкивают его в область более слабого поля.