
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Положение материальной точки в пространствеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Координаты точки Первый способ задать положение материальной точки - это задать ее координаты. Например, три числа xА, yА, zА задают положение точки A в декартовой системе координат.
Компоненты радиус-вектора На плоскости:
- x, y, z - компоненты радиуса - вектора. Очевидно, они же являются координатами материальной точки. Модуль радиус-вектора
3.6. Путь - длина отрезка траектории (3.5). 3.7. Перемещение - вектор, проведенный из начального положения (3.4.1), (3.4.2) материальной точки (3.1.1) в ее конечное положение.
Скорость направлена по касательной к траектории Так как
При приближении
Как известно из геометрии, касательная есть предельное положение секущей.
Значит, скорость направлена по касательной к траектории. Компоненты скорости На следующем рисунке изображен вектор скорости
Так как С другой стороны: откуда т.е. компоненты скорости равны производным соответствующих координат по времени. 3.8.3. Модуль скорости - производная пути по времени.
По теореме Пифагора: Вычисление пройденного пути Для равномерного движения
Для произвольного движения:
v1 в течение отрезка Δti приблизительно постоянны, если Δt достаточно мало.
т.е. путь - это определенный интеграл от модуля скорости по времени. 3.10. Ускорение - это производная скорости по времени.
Учитывая (3.8), получим:
Ускорение - вторая производная радиуса-вектора по времени. Производную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение - это скорость изменения скорости. Нормальное и тангенциальное ускорение Направим единичный вектор
Тогда
(по правилу нахождения производной от произведения). Первый член, нормальное ускорение,
показывает быстроту изменения направления скорости. Второй, тангенциальное ускорение,
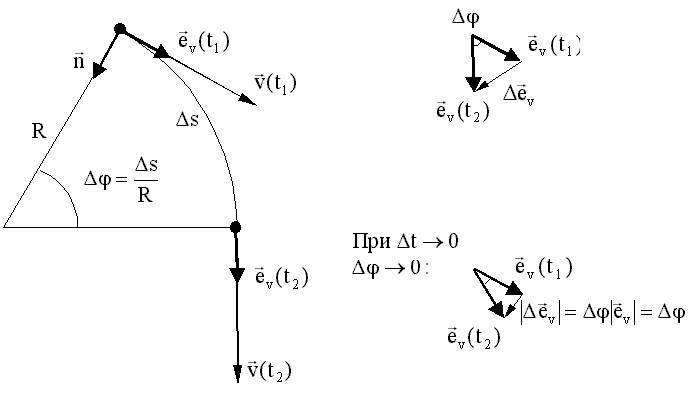
направлен вдоль скорости и показывает быстроту изменения ее модуля. Направление и величину нормального ускорения найдем для частного случая равномерного движения материальной точки по окружности:
Направлен
Нормальное ускорение направлено по нормали к скорости, его модуль:
Для движения по произвольной кривой R - радиус кривизны траектории - не будет величиной постоянной.
Динамика материальной точки 4.1. Почему в кинематике вводят только две производные от радиус-вектора:
А если ввести некую Можно, но обычно не нужно. Основная задача механики - предсказать положения тел в любой момент времени, т.е. предсказать вид функции Закон обнаруживается на более глубоком уровне - на уровне второй производной от радиус - вектора:
Двигаясь по этой цепочке "обратным ходом", мы можем, получив из закона природы (второй закон Ньютона) ускорение
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2017; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.223.185 (0.011 с.) |





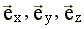 - единичные векторы или орты, направленные по осям x, y, z соответственно;
- единичные векторы или орты, направленные по осям x, y, z соответственно; - по теореме Пифагора.
- по теореме Пифагора.
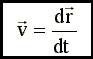 либо, применяя другое обозначение производной по времени,
либо, применяя другое обозначение производной по времени, 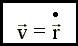
 , то направление вектора
, то направление вектора 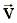 совпадает с предельным направлением вектора
совпадает с предельным направлением вектора  . На рис. а), б), в) показаны этапы предельного перехода для плоского движения (для простоты иллюстрации):
. На рис. а), б), в) показаны этапы предельного перехода для плоского движения (для простоты иллюстрации):
 к
к  ,
, 


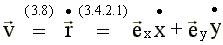 .
. ,
, , так же и
, так же и  ,
, .
. .
. ,
,  - весь путь,
- весь путь,  - весь отрезок времени,
- весь отрезок времени,  - const.
- const.
 .
.
 ,
, или
или 
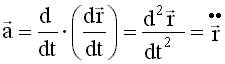
 вдоль вектора скорости:
вдоль вектора скорости: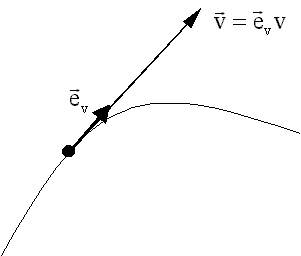



 , при
, при 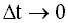 , по вектору
, по вектору  :
: .
. .
. .
. .
. .
. .
. .
. ?
? для всех изучаемых тел. Но в природе не существует фундаментального закона, что-либо утверждающего непосредственно о радиус-векторе материальной точки.
для всех изучаемых тел. Но в природе не существует фундаментального закона, что-либо утверждающего непосредственно о радиус-векторе материальной точки. - нет закона;
- нет закона;  - нет закона;
- нет закона;  - есть закон! →
- есть закон! → 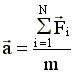 , см. (4.6).
, см. (4.6). , найти сначала
, найти сначала 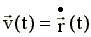 , затем и
, затем и  больше, чем два раза.
больше, чем два раза.


