
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика материальной точки.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Механика. Литература: 1. Савельев И.В. Курс общей физики. Т. 1,2. 2. Детлаф А.А., Яворский Б.М. Курс физики. 3. Волькенштейн В.С. Сборник задач по общему курсу физики, 1979 4. М/у Механика № 1885, электростатика № 1990.
Физические основы механики. Механика изучает простейший вид движения, который сводится к перемещению тел или частей тел относительно друг друга и называется механическим движением. Различают классическую, квантовую и релятивистскую механику. В классической механике рассматривается движение макротел, которые имеют скорость, меньшую, чем скорость света. В релятивистской – движение тел со скоростями, соизмеримыми со скоростью света. В квантовой – движение микрочастиц, размеры которых соизмеримы с размерами атомов или элементарных частиц. Механика подразделяется на кинематику, динамику и статику.
Кинематика материальной точки. В кинематике рассматривается механическое движение без выяснения причин, его вызывающих. Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени. При изучения механического движения реальных объектов в физике используются физические модели. Материальная точка – тело, размерами и формой которого можно пренебречь в условиях данной задачи. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел. Абсолютно твердое тело – тело, размеры и форма которого не меняются в процессе движения. Траектория – линия, вдоль которой материальная точка движется в пространстве в выбранной системе отсчета. По форме траектории движение можно разделить на прямолинейное и криволинейное. Длина пути – скалярная физическая величина, численно равная расстоянию, пройденному материальной точкой по её траектории от одного положения до другого.
Чтобы описать механическое движение тела, нужно знать его координаты в любой момент времени. Для определения координат материальной точки следует выбрать тело отсчета и связать с ним систему координат. Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела. Для описания многих движений систему отсчета связывают с Землей, считая ее неподвижной. В ряде случаев в качестве тела отсчета выбирают Солнце или отдаленные звезды. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно. Положение частицы в пространстве можно задать двумя способами: 1) указав радиус-вектор частицы (
Поступательное движение – механическое движение, при котором прямая, проведенная через две произвольные точки тела, перемещается параллельно самой себе. Для описания поступательного движения достаточно выбрать одну точку и описать ее движение. Вращательное движение - движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой. Основными кинематическими характеристиками движения материальной точки являются скорость и ускорение. График скорости Из уравнения
Основные виды движения 1. аn = 0, at = 0 – прямолинейное равномерное движение; 2. аn = 0, at = const – прямолинейное равнопеременное движение; 3. аn = 0, at ¹ 0 – прямолинейное с переменным ускорением; 4. аn = const, at = 0 – равномерное по окружности 5. аn = const, at = const – равнопеременное по окружности 6. аn ¹ const, at ¹ const – криволинейное с переменным ускорением. Период и частота Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодам обращения (Т). Т.к. длина окружности равна 2pR, период обращения при равномерном движении тела со скоростью v по окружности радиусом R равняется:
Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:
Динамика частиц Динамика рассматривает механическое движение с учетом причин, вызывающих это движение или изменение этого движения. Основная задача динамики: для физической системы, находящейся в определенных внешних условиях, найти уравнение движения. Уравнениями движения называются уравнения, описывающие изменение состояния системы во времени. В классической механике состояние частиц полностью определяется заданием ее координат x, y, z и составляющих скорости vx, vy, vz, т.е. заданием радиус-вектора Состояние системы из N нерелятивистских частиц определяется заданием радиус-векторов В самом общем виде уравнения движения системы частиц может быть записано в виде
Вид функции Общее решение уравнения может быть найдено, если известны: 1) вид функции 2) начальные условия, т.е. значения
Механические системы Механической системой называется совокупность материальных точек (тел), рассматриваемых как единое целое. Тела, не входящие в состав исследуемой механической системы, называются внешними телами. Силы, действующие на систему со стороны внешних тел, называются внешними силами. Внутренними силами называются силы взаимодействия между частями рассматриваемой системы. Механическая система называется замкнутой, или изолированной, системой, если она не взаимодействует с внешними телами (на нее не действуют внешние силы). Тело называется свободным, если на его положение и движение в пространстве не наложено никаких ограничений, и – несвободным – если на его возможные положения и движения наложены те или иные ограничения, называемые в механике связями. Несвободное тело можно рассматривать как свободное, заменив действие на него тел, осуществляющих связи, соответствующими силами. Эти силы называются реакциями связей, а все остальные силы, действующие на тело, - активными силами.
Масса. Импульс Масса – физическая величина, одна из основных характеристик материи, определяющая ее инерционные и гравитационные свойства. Единица массы в СИ – килограмм (кг) Векторная величина
Силы в механике Силы упругости. Силы упругости возникают в результате взаимодействия тел, сопровождающегося их деформацией. Упругая сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия:
где Примером силы упругости является сила упругости деформации пружины при растяжении или сжатии:
где k – жесткость пружины, x – упругая деформация. Сила трения скольжения. Сила трения скольжения возникает при скольжении одного тела по поверхности другого:
где k – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей, N – сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила трения скольжения направлена по касательной к трущимся поверхностям в сторону, противоположную движению рассматриваемого тела относительно другого. III закон Ньютона Рассмотрим замкнутую систему, состоящую из двух частиц, взаимодействующих с силами Для замкнутой системы справедлив закон сохранения импульса:
Дифференцируя это соотношение по времени
На основании (3) получим III закон Ньютона: Всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки. Как и II закон Ньютона, он выполняется только в инерциальных системах отсчета. Кинетическая энергия Энергия – это универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную… Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Пусть частица массы m движется под действием переменной силы F, которая сообщает ей ускорение
Учитывая, что
Величина Кинетическая энергия механической системы (Т) – это энергия механического движения этой системы. Следовательно, работа результирующей силы равна приращению кинетической энергии точки:
Твердое тело в механике. Интервал. Всякое событие происходит в пространстве и во времени и характеризуется тремя пространственными координатами x,y,z и одной временной координатой t. Поэтому для изучения динамики различных процессов часто пользуются воображаемым четырехмерным пространством, на осях которого откладывают координаты x,y,z и время t (четырехмерный мир Минковского). Рассмотрим в четырехмерном пространстве два события: первое имеет координаты x1, y1, z1, t1, второе – x2, y2, z2, t2. Величину
называют интервалом между событиями. Покажем, что интервал между двумя данными событиями одинаков во всех инерциальных системах отсчета. Для этого запишем (75) в двух инерциальных системах отсчета, движущихся относительно друг друга со скоростью
и
Из преобразований Лоренца следует, что:
Подставим (78) а (77) т.к.
умножим на с2:
откуда следует, что
Понятие интервала устанавливает связь между пространственными и временными координатами событий. Как следует из (79), величина интервала не меняется при переходе от одной инерциальной системы отсчета к другой. Этот вывод вытекает из условия, что скорость света одинакова во всех инерциальных системах. Поэтому (79) представляет собой математическое выражение постулата о постоянстве скорости света. Собственное время. Время, отсчитанное по часам, движущимся вместе с данным объектом, называется собственным временем объекта. Собственное время принято обозначать через
Покажем, что собственное время инвариантно относительно преобразований Лоренца, т.е. одинаково во всех инерциальных системах отсчета. Свяжем с инерциальной системой отсчета часы. Т.к. часы покоятся в этой системе, то:
и интервал между событиями в этой системе равен:
а собственное время:
Ранее было показано, что Релятивистский импульс Ранее была установлена инвариантность законов Ньютона, следовательно, и вытекающего из них закона сохранения импульса относительно преобразований Галилея. Однако инвариантность этих законов по отношению к преобразованиям Лоренца не соблюдается. В СТО найдено новое выражение для импульса частицы, такое что 1) закон сохранения импульса остается инвариантным по отношению к преобразованиям Лоренца как при больших, так и при малых скоростях и 2) при Рассмотрим частицу, движущуюся со скоростью
Допустим, что
Величина
называется массой движущегося тела или релятивистской массой. Из (84) следует, что при
Связь энергии и импульса. Соотношение
В числителе прибавим и отнимем
Или
Отсюда получим:
или:
Т.к.
Из формул
легко получить еще одно соотношение, связывающее энергию и импульс частицы в релятивистской механике:
Инварианты преобразования. При изучении СТО мы установили существование целого ряда инвариантных величин, т.е. величин, не меняющихся при переходе от одной инерциальной системы отсчета к другой. Перечислим их: 1. скорость света в вакууме (с); 2. интервал между событиями: 3. собственное время 4. масса покоя Покажем, что существует еще один инвариант
Откуда:
т.к. масса покоя и скорость света инвариантны относительно преобразований Лоренца. Из (100) следует, что в СТО все законы сохранения энергии и импульса перестают быть независимыми, а объединяются в единый закон сохранения импульса-энергии. Механика. Литература: 1. Савельев И.В. Курс общей физики. Т. 1,2. 2. Детлаф А.А., Яворский Б.М. Курс физики. 3. Волькенштейн В.С. Сборник задач по общему курсу физики, 1979 4. М/у Механика № 1885, электростатика № 1990.
Физические основы механики. Механика изучает простейший вид движения, который сводится к перемещению тел или частей тел относительно друг друга и называется механическим движением. Различают классическую, квантовую и релятивистскую механику. В классической механике рассматривается движение макротел, которые имеют скорость, меньшую, чем скорость света. В релятивистской – движение тел со скоростями, соизмеримыми со скоростью света. В квантовой – движение микрочастиц, размеры которых соизмеримы с размерами атомов или элементарных частиц. Механика подразделяется на кинематику, динамику и статику.
Кинематика материальной точки. В кинематике рассматривается механическое движение без выяснения причин, его вызывающих. Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени. При изучения механического движения реальных объектов в физике используются физические модели. Материальная точка – тело, размерами и формой которого можно пренебречь в условиях данной задачи. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел. Абсолютно твердое тело – тело, размеры и форма которого не меняются в процессе движения. Траектория – линия, вдоль которой материальная точка движется в пространстве в выбранной системе отсчета. По форме траектории движение можно разделить на прямолинейное и криволинейное. Длина пути – скалярная физическая величина, численно равная расстоянию, пройденному материальной точкой по её траектории от одного положения до другого.
Чтобы описать механическое движение тела, нужно знать его координаты в любой момент времени. Для определения координат материальной точки следует выбрать тело отсчета и связать с ним систему координат. Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела. Для описания многих движений систему отсчета связывают с Землей, считая ее неподвижной. В ряде случаев в качестве тела отсчета выбирают Солнце или отдаленные звезды. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно. Положение частицы в пространстве можно задать двумя способами: 1) указав радиус-вектор частицы (
Поступательное движение – механическое движение, при котором прямая, проведенная через две произвольные точки тела, перемещается параллельно самой себе. Для описания поступательного движения достаточно выбрать одну точку и описать ее движение. Вращательное движение - движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой. Основными кинематическими характеристиками движения материальной точки являются скорость и ускорение.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.70 (0.011 с.) |


 ), 2) указав координаты частицы (x, y, z).
), 2) указав координаты частицы (x, y, z).
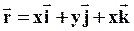 ,
где
,
где  ,
,  и
и  - орты, или единичные векторы, задающие направление осей координат.
- орты, или единичные векторы, задающие направление осей координат.
 следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю, то прямая проходит через начало координат.
следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю, то прямая проходит через начало координат.


 (с-1)
(с-1) и скорости
и скорости  .
. ,
,  , …,
, …, 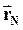 и скоростей
и скоростей  ,
,  , …,
, …, 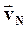 всех частиц в данный момент времени.
всех частиц в данный момент времени.
 зависит от свойств частиц системы и внешних условий, в которых они движутся
зависит от свойств частиц системы и внешних условий, в которых они движутся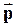 , равная произведению массы m материальной точки на ее скорость
, равная произведению массы m материальной точки на ее скорость  , и имеющая направление скорости, называется импульсом, или количеством движения, этой материальной точки:
, и имеющая направление скорости, называется импульсом, или количеством движения, этой материальной точки:



 и
и  ,
,  и
и  - импульсы этих частиц.
- импульсы этих частиц.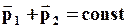

 или
или  (21)
(21) :
:
 Скорость частицы в точке А обозначим через
Скорость частицы в точке А обозначим через 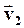 , причем v2>v1.
Работа силы
, причем v2>v1.
Работа силы  на пути АВ (АВ=S) равна:
на пути АВ (АВ=S) равна:

 , получим:
, получим: (25)
(25) называется кинетической энергией точки.
называется кинетической энергией точки. .
. (75)
(75) , в следующем виде:
, в следующем виде: (76)
(76) (77)
(77) ;
;  ;
;  ;
;  ; (78)
; (78) :
:



 или
или  (79)
(79) . Получим выражение для собственного времени
. Получим выражение для собственного времени  :
: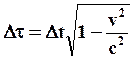 (80)
(80) ;
;  ;
;  ,
,
 (81)
(81) и
и  одинаковы во всех инерциальных системах отсчета, поэтому
одинаковы во всех инерциальных системах отсчета, поэтому  остается справедливым ньютоновское определение импульса.
остается справедливым ньютоновское определение импульса. - вектор перемещения частицы за время
- вектор перемещения частицы за время  . Умножим
. Умножим  , где
, где  - собственное время частицы,
- собственное время частицы,  - некоторая постоянная:
- некоторая постоянная: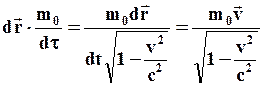 (82)
(82) можно пренебречь, и возьмем в качестве
можно пренебречь, и возьмем в качестве  перейдет в
перейдет в  . В классической механике этот вектор, как известно, называют импульсом частицы. Поэтому в релятивистской механике естественно импульс определить выражением:
. В классической механике этот вектор, как известно, называют импульсом частицы. Поэтому в релятивистской механике естественно импульс определить выражением: (83)
(83) (84)
(84)
 ;
;  возведем в квадрат.
возведем в квадрат. (95)
(95) :
:
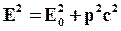
 (96)
(96) (97)
(97) , то
, то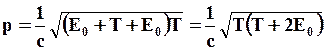 (98)
(98)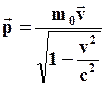 и
и 
 (99)
(99) ;
; . Из уравнения (95) следует, что:
. Из уравнения (95) следует, что:
 (100)
(100)


