
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Длительность событий в различных инерциальных системах отсчета.Содержание книги
Поиск на нашем сайте
По отношению к системе Oxyz т. A движется, начало события происходит в т.
где Моменты начала
откуда получим:
Из (69) следует, что Dt0<Dt, т.е. длительность события наименьшая в той системе, по отношению к которой т. A покоится. Это значит, что процессы в движущейся системе протекают медленнее, чем в неподвижной, движущиеся часы идут медленнее неподвижных.
Релятивистский закон сложения скоростей. Обозначим:
Как известно,
и Из преобразований Лоренца найдем:
Разделив первые три равенства (72) на четвертое и используем (70) и (71):
Легко видеть, что при
Интервал. Всякое событие происходит в пространстве и во времени и характеризуется тремя пространственными координатами x,y,z и одной временной координатой t. Поэтому для изучения динамики различных процессов часто пользуются воображаемым четырехмерным пространством, на осях которого откладывают координаты x,y,z и время t (четырехмерный мир Минковского). Рассмотрим в четырехмерном пространстве два события: первое имеет координаты x1, y1, z1, t1, второе – x2, y2, z2, t2. Величину
называют интервалом между событиями. Покажем, что интервал между двумя данными событиями одинаков во всех инерциальных системах отсчета. Для этого запишем (75) в двух инерциальных системах отсчета, движущихся относительно друг друга со скоростью
и
Из преобразований Лоренца следует, что:
Подставим (78) а (77)
т.к.
умножим на с2:
откуда следует, что
Понятие интервала устанавливает связь между пространственными и временными координатами событий. Как следует из (79), величина интервала не меняется при переходе от одной инерциальной системы отсчета к другой. Этот вывод вытекает из условия, что скорость света одинакова во всех инерциальных системах. Поэтому (79) представляет собой математическое выражение постулата о постоянстве скорости света. Собственное время. Время, отсчитанное по часам, движущимся вместе с данным объектом, называется собственным временем объекта. Собственное время принято обозначать через
Покажем, что собственное время инвариантно относительно преобразований Лоренца, т.е. одинаково во всех инерциальных системах отсчета. Свяжем с инерциальной системой отсчета часы. Т.к. часы покоятся в этой системе, то:
и интервал между событиями в этой системе равен:
а собственное время:
Ранее было показано, что Элементы релятивистской динамики. Релятивистский импульс Ранее была установлена инвариантность законов Ньютона, следовательно, и вытекающего из них закона сохранения импульса относительно преобразований Галилея. Однако инвариантность этих законов по отношению к преобразованиям Лоренца не соблюдается. В СТО найдено новое выражение для импульса частицы, такое что 1) закон сохранения импульса остается инвариантным по отношению к преобразованиям Лоренца как при больших, так и при малых скоростях и 2) при Рассмотрим частицу, движущуюся со скоростью
Допустим, что
Величина
называется массой движущегося тела или релятивистской массой. Из (84) следует, что при
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.175.189 (0.007 с.) |


 - длительность события в системе O’x’y’z’.
- длительность события в системе O’x’y’z’. , а конец в т.
, а конец в т.  , причем:
, причем: (68)
(68) - длительность события в системе Oxyz.
- длительность события в системе Oxyz. и конца
и конца  события должны быть отмечены по синхронизированным часам системы Oxyz, находящимся в точках
события должны быть отмечены по синхронизированным часам системы Oxyz, находящимся в точках 
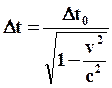 (69)
(69) - скорость некоторой т. A в системе отсчета Oxyz;
- скорость некоторой т. A в системе отсчета Oxyz; - скорость той же точки в системе отсчета O’x’y’z’, движущейся вдоль оси x со скоростью
- скорость той же точки в системе отсчета O’x’y’z’, движущейся вдоль оси x со скоростью  .
. ;
;  ;
;  (70)
(70) ;
;  ;
;  (71)
(71) ;
;  ;
;  ;
;  ; (72)
; (72)



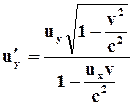



 и
и  релятивистский закон сложения скоростей переходит в классический.
релятивистский закон сложения скоростей переходит в классический. (75)
(75) (76)
(76) (77)
(77) ;
;  ;
;  ;
;  ; (78)
; (78) :
:



 или
или  (79)
(79) . Получим выражение для собственного времени
. Получим выражение для собственного времени  :
: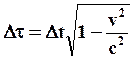 (80)
(80) ;
;  ;
;  ,
,
 (81)
(81) и
и  одинаковы во всех инерциальных системах отсчета, поэтому
одинаковы во всех инерциальных системах отсчета, поэтому  относительно неподвижной инерциальной системы отсчета;
относительно неподвижной инерциальной системы отсчета;  - вектор перемещения частицы за время
- вектор перемещения частицы за время  . Умножим
. Умножим  , где
, где  - собственное время частицы,
- собственное время частицы,  - некоторая постоянная:
- некоторая постоянная: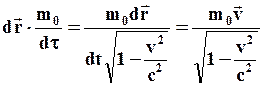 (82)
(82) можно пренебречь, и возьмем в качестве
можно пренебречь, и возьмем в качестве  перейдет в
перейдет в  . В классической механике этот вектор, как известно, называют импульсом частицы. Поэтому в релятивистской механике естественно импульс определить выражением:
. В классической механике этот вектор, как известно, называют импульсом частицы. Поэтому в релятивистской механике естественно импульс определить выражением: (83)
(83) (84)
(84)
 ;
; 


