
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проекции скорости и ускоренияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме. Векторы начальной скорости Известно, что проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось.
График скорости Из уравнения
Основные виды движения 1. аn = 0, at = 0 – прямолинейное равномерное движение; 2. аn = 0, at = const – прямолинейное равнопеременное движение; 3. аn = 0, at ¹ 0 – прямолинейное с переменным ускорением; 4. аn = const, at = 0 – равномерное по окружности 5. аn = const, at = const – равнопеременное по окружности 6. аn ¹ const, at ¹ const – криволинейное с переменным ускорением. Вращательное движение твердого тела. Вращательное движение твердого тела относительно неподвижной оси – движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения. Равномерное движение по окружности Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению. При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости
Из подобия треугольников OAB и BCD следует
Если интервал времени ∆t мал, то мал и угол a. При малых значениях угла a длина хорды AB примерно равна длине дуги AB, т.е.
Поскольку
Период и частота Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодам обращения (Т). Т.к. длина окружности равна 2pR, период обращения при равномерном движении тела со скоростью v по окружности радиусом R равняется:
Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:
Кинематика вращательного движения
Для указания направления вращения малым углам поворота приписывают направление:
Мгновенная угловая скорость:
или
в векторной форме:
Угловое ускорение вращающегося тела Отношение
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.01 с.) |

 и ускорения
и ускорения  могут иметь различные направления, поэтому переход от векторной записи уравнений к алгебраической может оказаться весьма трудоемким.
могут иметь различные направления, поэтому переход от векторной записи уравнений к алгебраической может оказаться весьма трудоемким.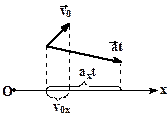
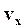 вектора скорости
вектора скорости  на произвольную ось OX нужно найти алгебраическую сумму проекций векторов
на произвольную ось OX нужно найти алгебраическую сумму проекций векторов  на ту же ось.
на ту же ось.
 Проекцию вектора на ось считают положительной, если от проекции начала к проекции конца вектора нужно идти по направлению оси, и отрицательной в противоположном случае.
Проекцию вектора на ось считают положительной, если от проекции начала к проекции конца вектора нужно идти по направлению оси, и отрицательной в противоположном случае.




 . Этот путь равен длине дуги AB. Векторы скоростей
. Этот путь равен длине дуги AB. Векторы скоростей  и
и  в точках A и Bнаправлены по касательным к окружности в этих точках, а угол a между векторами
в точках A и Bнаправлены по касательным к окружности в этих точках, а угол a между векторами  и определим отношение изменения скорости к ∆t:
и определим отношение изменения скорости к ∆t:


 . Т.к.
. Т.к.  ,
, 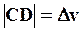 , то получаем
, то получаем
 .
.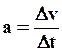 , то получаем
, то получаем

 (с-1)
(с-1)
 за время Dt пройдет путь равный длине дуги DS, а радиус вектор
за время Dt пройдет путь равный длине дуги DS, а радиус вектор 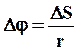 называется углом поворота радиус-вектора выбранной точки от некоторого начального положения или модулем углового перемещения.
называется углом поворота радиус-вектора выбранной точки от некоторого начального положения или модулем углового перемещения.
 направлен по оси вращения так, чтобы рассматриваемое с его конца вращение происходило против часовой стрелки (правило правого винта). Если тело сделало N поворотов:
направлен по оси вращения так, чтобы рассматриваемое с его конца вращение происходило против часовой стрелки (правило правого винта). Если тело сделало N поворотов: 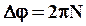 . Средняя угловая скорость:
. Средняя угловая скорость: (11)
(11) (12)
(12)
 связано с углом поворота правилом правого винта. Размерность – рад/с.
Если тело делает n оборотов в сек, то его угловая скорость
связано с углом поворота правилом правого винта. Размерность – рад/с.
Если тело делает n оборотов в сек, то его угловая скорость  .
Связь линейной и угловой скоростей:
.
Связь линейной и угловой скоростей:
 ;
;
 (13)
(13) (14)
(14) называется средним угловым ускорением.
называется средним угловым ускорением.
 (15)
Вектор углового ускорения
(15)
Вектор углового ускорения  направлен по оси вращения, причем при ускоренном вращении
направлен по оси вращения, причем при ускоренном вращении  , при замедленном вращении
, при замедленном вращении 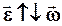 .
.



