
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние упругости опор на критические скоростиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
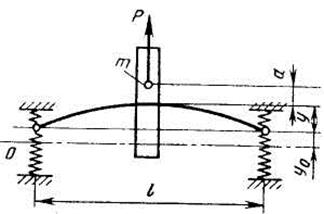
Рассмотрим схему ротора (рис. 7.4), когда опоры вала обладают упругостью, которая оценивается общим коэффициентом c0. Условие равновесия для этой схемы определяется равенствами
Приравняв знаменатель нулю, определим критическую скорость для ротора на упругих опорах:
Полученная формула показывает, что введение упругих опор ротора снижает его критическую скорость. Это позволяет устранить критическую скорость ротора из области его угловых рабочих скоростей и снизить усилия на опорах.
Рис. 7.4. Симметричный ротор на упругих опорах 3. Напряжения растяжения от инерционных сил. Центробежная сила элементарного участка лопатки протяженностью dr(рис. 5.3), выражается формулой
напряжение растяжения
(5.3) Для того чтобы оценить характер распределения напряжений растяжения по длине лопатки, используется некоторый осредненный закон распределения площадей
где F0— площадь поперечного сечения лопатки в корневом сечении; q— показатель, определяющий степень изменения площадей по длине лопатки;a— коэффициент, зависящий от соотношения площадей на конце лопатки и в корневом сечении. Согласно формуле (5.4) он равен
Напряжение растяжения в сечении будет равно
(5.9). Если лопатки имеют бандажную полку, то напряжения растяжения, создаваемые бандажной полкой, складываются с напряжениями от собственной массы лопатки. Напряжения от бандажной полки определяются по формуле
(5.10)где Рб— центробежная сила бандажной полки — величина постоянная для всех сечений лопатки, лежащих ниже бандажной полки:
4 Колебание дисков. При проектировании легких дисков турбин и компрессоров с весьма незначительной толщиной стенок, появляется возможность возникновения опасных резонансных колебаний или автоколебаний дисков. Огромные резонансные или автоколебательные всплески напряжений приводят к разрушению дисков несмотря на наличие вполне достаточных запасов статической прочности. Поэтому необходимо уделять большое внимание динамической прочности дисков. Спектр собственных форм колебаний в первом приближении можно представить с помощью круглых пластин (рис. 6.29). Формы колебаний отличаются друг от друга числом узловых диаметров n и числом узловых окружностей S. В соответствии этими признаками все формы разделяются на три группы. К 1-ой группе относятся осесимметричные формы колебаний (иногда называемые зонтичными). Для этих форм характерно отсутствие узловых диаметров (n=0). Внутри группы формы отличаются числом узловых окружностей (S= 0, 1, 2, 3). Особенностью осесимметричных форм является их неуравновешенность в осевом направлении.
Рис. 6.32. Формы колебаний дисков ротора компрессора и турбины: а — колебания центральной части дисков: 1- первая форма; 2 — вторая форма; б—раздельные колебания: 1— периферийных частей дисков с лопатками, 2 - центральных частей: в — совместные колебания дисков, лопаток и барабанной оболочки; г — колебания диска турбины
5 КОЛЕБАНИЯ ЛОПАТОК. Колебания лопаток создают большие дополнительные динамические напряжения в них, вызывают усталостные явления в материале. Вследствие этого с течением времени в различных местах лопаток появляются трещины, происходит их разрушение. Лопатка, как всякая упругая конструкция, обладает спектром собственных частот и форм колебаний. Эти показатели являются определяющими, так как полностью представляют динамические свойства лопаток. Резонансные колебания и факторы, влияющие на них, исследуются экспериментально и при натурных испытаниях двигателей. Виды и формы колебаний лопаток. Если лопатку представить весьма упрощенно, в виде плоской пластины, закрепленной в виде заделки с одной стороны (рис. 5.28), то можно разделить формы колебаний лопаток на три вида: изгибные, крутильные и пластиночные. Внутри каждого вида формы отличаются числом поперечных узловых линий и имеют соответствующую нумерацию: первая форма без поперечных узловых линий, вторая — с одной, третья — с двумя линиями и т. д. Каждая форма имеет свою определенную частоту собственных колебаний, зависящую от размеров лопатки.
Рис. 5.28. Формы колебаний лопатки. а — изгибные формы, б — крутильные формы, в — пластиночные формы Изгибные формы являются наиболее широкой разновидностью колебаний лопаток. Они всегда присут-ствуют на работающем двигателе. Из-за многообразия форм практически не представляется возможным избавиться от всех форм колебаний в пределах рабочих частот вращения рабочих колес компрессоров и турбин. Если центры тяжести сечений лопатки не лежат на общей радиальной оси, то изгибные колебания сопровождаются крутильными деформациями лопаток. Если лопатка имеет естественную закрутку, то ее колебания становятся пространственными, но изгибный характер сохраняется. 7 Расчет дисков методом кольцевых элементов. Диск произвольной формы разбивается сечениями на кольцевые элементы со следующими условиями: каждое кольцо имеет постоянную толщину; в пределах кольца температура изменяется по закону: T=Ti+Ti+1-Ti/ri+1-ri/
Последовательность расчетов: 1. Исходные и не радиальные сечения разбиваются на систему колец, причем у дисков с центральным отверстием первое сечение нач-ся r1 =(0,01...0,05)б 2. Замковая часть в расчетах не учитывается, т.к. в ней действует много факторов. 3. Задается температура на границе диска в 1-ых и n-ых сечениях. Tn=Tкорн-(100..200). причем Tn- Tкорн <450..500.расчитывается температура по формуле: Ti=T1+(Tn-T1)(ri-r1/rn-r1)^m m=2-для неохлажд-его диска m=3- для охлаждаемого диска. По значениям Т выбираем Е, α, σ. 4. Определ-ся радиальные напряжения в n-ом сечении σr=(Pл*z+(2Пr-f)ρrω2)/((2Пrh) 4. Задаются условия для 1-ого и 2-ого расчетов σ 1Ө, σ 1r. σ 2 Ө . σ 2 r. для диска с центральным отверстием σ 1r=. σ 2 r дл диска без центр. отв. σ 1Ө= σ 1r σ 2 Ө= σ 2 r. 5. Произ-ся 1-ый расчет и опред-ся σ 1Ө,σ 1r. 6. Произ-ся 2-ой расчет при условии ω=0; ΔTi=0 7. φ- опред-ся коэф-т согласия напряжений. φ=σrn- σ 1rn/ σ 2rn 8. Определ-ся напр. в i-ом сечении σ Ө= σ 1Ө+φ σ 2Ө σ r= σ 1r+φ σ 2r 9. Определяем расчетное знач. напря-ий как средние по сечению σ Ө расч=0,5(σ Өi+ σ iӨ) 10. Определяем запас прочности в сечениях κ=σдл/σэкв σэкв= σ1-λ σ3 λ- коэф-ет предела длител-ой прочности при растяжении или сжатии 8 Определение изгибающих моментов и напряжений от действия газодинамических сил. Изгибающие моменты определяются на основании треугольников скоростей и статических давлений перед и за рабочим колесом в проекциях на координатные оси х, у, z. Примем правую систему осей координат (рис. 5.8). Начало координат помещается в центр инерции корневого сечения. (Рис. 5.8. К расчету лопатки на изгиб: 1— ось ротора) Ось х направ-лена параллельно оси ротора в сторону осевой ско-рости воздуха, ось у — в сторону, противоположную окружной скорости касательно к окружности кор-невых сечений лопаток. Ось z является радиальной осью. Методика определения изгибающих моментов является общей для компрессоров и турбин. В практических расчетах отличие состоит в знаках и величинах определяющих скоростей, давлений и получаемых моментов. Интенсивность давления на лопатку аэродинамических сил в проекциях на координатные плоскости обозначим qxи qy. Она определяется формулами
Где tz— шаг лопатки по окружности с координатой z, равный 2πrs / n; n — число лопаток; p, ρ, ca, cu—статическое дав-ление, плотность газа, осевые и окружные скорости за и перед рабочим колесом соответственно треугольникам скоростей; ρ1* c1a — массовый рас-ход рабочего тела через лопаточную машину, отнесенную к единице проходного сечения. 1- ый член в формуле (5.11) представляет собой разность статических давлений на участок лопатки, равный единице. Второй член — сила реакции, равная изменению количества движения воздуха или газа под действием лопаток. В направлении оси у интенсивность qy определяется только изменением количества движения. Выделим на лопатке элементарный участок протяженностью dz (рис. 5.9). Компоненты газодинамических сил, действующие на элементарный участок, равны qxdzи qydz. Элементарные моменты, создаваемые этими силами в сечении с координатой z1, определяются формулами
(5.13) Напряжения изгиба в любой точке расчетного сечения профиля определяются изгибающими моментами Mξ и Mη, действующими по главным осям. Эти моменты находим как сумму проекций изгибающих моментов Mx и My, рассчитанных по формулам (5.14):
Напряжение изгиба в любой точке s на контуре профиля или внутри его, имеющей координаты ξ,η определяется по формуле
Где Jξ, Jη — моменты инерции сечения относи-тельно главных осей. Величина и знак напряжения зависят от положения точки s, от знака и величины изгибающих моментов. Как было показано, изгибающие моменты для лопатки турбины имеют положительный знак, а для лопатки компрессора — отрицательный (см. рис. 5.10). Наибольшие напряжения возникают в точках А, В, С — наиболее удаленных от оси ξ. В точках А и B как у турбинных, так и у компрессорных лопаток действуют напря-жения растяжения, а на спинке лопатки — в точке С — напряжения сжатия. Напряжения изгиба склады-ваются с учетом знака с напряжениями растяжения.
9 Опред-ние осевых газовых сил. Осевое усилие, возник-щее на элементах констр-ций двигателей, опред-ся как ∑ статических давлений воздуха или газа на поверх-ти проточной части элем-ов и газодинам-ской силы, вызванной изменением количества движения воздуха или газа при прохож-нии его ч/з рассматр-мый элемент конструкции. Входное устройство двига-теля. Осевая сила, действующая на входное устройство двигателя с осевым компрессором (рис. 2.5), согласно общему определению, рассчитывается по формуле Где р1, р2— статические давления в потоке перед и за входным устройством; р3— статическое давление в полости за задним торцом внутреннего обтекателя; может отличаться от р2. Граница, разделяющая зоны давлений р2 и р3, проходит по окружности расположения лабиринтного уплотнения; с1а, с2а— осевые скорости потока на входе и выходе входного устройства; G— масса воздуха, проходящего через входное устройство, кг/с; Paвнеш—осевое (горизонтальная составляющая) усилие от давления воздуха на внешнюю поверхность входного устройства; определяется продувкой.
10 УСИЛИЯ, ДЕЙСТВУЮЩИЕ В ГАЗОТУРБИННЫХ ДВИГАТЕЛЯХ. На силовые элементы конструкций газотурбинного двигателя действуют разнообразные нагрузки в виде сил и моментов. основные нагрузки можно разделить на следующие группы: 1) газовые нагрузки, возникающие как результат воздействия газового потока на элементы проточной части двигателя и газостатические нагрузки; 2) массовые нагрузки, к которым относятся силы инерции и инерционные моменты, возникающие в деталях при вращении ротора, при эволюциях самолета, при взлете и посадке; 3) температурные нагрузки, возникающие из-за неравномерного нагрева деталей, различия коэффициентов линейного расширения их материалов, при стеснении температурных деформаций. В зависимости от направления действия нагрузки могут быть разделены на осевые, поперечные, действующие в вертикальной и горизонтальной плоскостях.. Перечисленные нагрузки воспринимаются силовыми элементами корпуса и ротора, частично замыкаются и уравновешиваются в пределах двигателя, а частично передаются на узлы крепления двигателя к самолету. Инерционные силы. При выполнении самолетом эволюции в полете, а также при взлете и посадке возникают инерционные перегрузки, действующие на все элементы двигателя
где М — масса узла, детали или двигателя в целом, в кг; nэmax— коэффициент максимальной эксплуатационной перегрузки. Гироскопические моменты. При выполнении самолетом эволюцией на вращающийся ротор двигателя кроме сил инерции, вызывающих перегрузку, действует гироскопический момент.
где Jp — массовый полярный момент инерции ротора относительно оси его вращения; ω— угловая скорость ротора; Ω— угловая скорость самолета при эволюции;θ — угол между векторами угловых скоростей ω и Ω.
11 расчет на прочность дисков турбин. Основной нагрузкой являе-ся центробежная сила лопаток, собственная масса диска и присоединенных к диску элементов. В дисках турбины возникают доп-ые напр-ия вследствии неравномерного распределения тем-ры по радиусу. Целью расчета является определение распределения окр-ых и радиал-ых усилий в диске, радиал-ых деформаций и запасов прочности. Основные допущения: 1. Рассмат-ся симметричная форма диска. 2. Диск является осесимметрчным телом наличие отверстий и бобышек отдельных выступов и протчек не учитываятся. 3. Контурная нагрузка от центр-ых сил лопаток, дейст-ет в плоскости симметрии и равномерно распред-а по всей поверхности внеш-го контура. 4. температура изменяется только по радиусу диска и равномерно распред-ны по его толщине 5. по тлщине диска напряжения енеизменны, осевые напряжения =0. вывод расч-ых урав-ий:
Выделим в диске перм-ой толщины бесконечно малый элемент (см. рис.) Огран-ый 2-мя плоскостями прох-ми ч/з ось вращения и образующие м/у собой угол dӨ и 2-ия цилиндр-ми поверхностями r и r+dr. Действия отброш-ых частей диска заменим напряжениями σr,σ r+dr,Усилие, возникающее на контуре элемента равны произведению действующего напряжения на величину площадки, кроме контурных сил на элемнт действует центроб-ая сила собст-ой массы элемента: dP=rω2dm Упругие и темпер-ые деформации будут равны: ε=1/E(σr-μσӨ)+αT 1-ый член упругая деформация, 2-ой член температурное напряжение
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 635; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.61.184 (0.014 с.) |

 (7.6) где у0 — смещение в упругих опорах; у— прогиб вала; а— эксцентриситет; с0— коэффициент жесткости упругой опоры. Решив эти равенства относительно у, получим
(7.6) где у0 — смещение в упругих опорах; у— прогиб вала; а— эксцентриситет; с0— коэффициент жесткости упругой опоры. Решив эти равенства относительно у, получим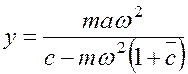 где
где  . (7.7)
. (7.7)
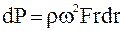 (5.1)где ρ — плотность материала; ω— угловая скорость колеса; F— площадь поперечного сечения лопатки на радиусе r.
(5.1)где ρ — плотность материала; ω— угловая скорость колеса; F— площадь поперечного сечения лопатки на радиусе r.
 (5.4)
(5.4)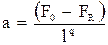 (5.5)
(5.5)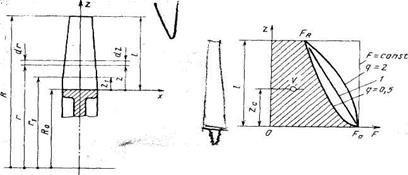 за счет профилирования сечений лопатки по ее длине масса уменьшается почти в два раза. Это позволяет уменьшить центробежную силу лопатки, напряжения растяжения и увеличить окружную скорость рабочего колеса. Формулу для расчета растягивающей инерционной силы, действующей в сечении лопатки с координатой z1, получим из (5.2), подставив в нее функцию площади (5.4) и заменив
за счет профилирования сечений лопатки по ее длине масса уменьшается почти в два раза. Это позволяет уменьшить центробежную силу лопатки, напряжения растяжения и увеличить окружную скорость рабочего колеса. Формулу для расчета растягивающей инерционной силы, действующей в сечении лопатки с координатой z1, получим из (5.2), подставив в нее функцию площади (5.4) и заменив  :
:
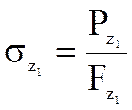
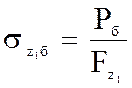
 Здесь Мб— масса бандажной полки; rб— радиус расположения ее центра инерции сечения площади поперечного сечения лопатки в направлении от корневого сечения к ее концу уменьшаются, напряжения от действия бандажной полки растут. Это выравнивает напряжения, и наиболее рациональный закон профилирования лопатки становится близким к q=1. Напряжения растяжения для лопаток являются основными. Они составляют в среднем 50... 70 % общего напряжения. При этом, что очень важно, они действуют по всему сечению лопатки, но не в отдельных точках. Поэтому приближенная оценка лопатки часто производится по напряжениям растяжения, с полным расчетом.
Здесь Мб— масса бандажной полки; rб— радиус расположения ее центра инерции сечения площади поперечного сечения лопатки в направлении от корневого сечения к ее концу уменьшаются, напряжения от действия бандажной полки растут. Это выравнивает напряжения, и наиболее рациональный закон профилирования лопатки становится близким к q=1. Напряжения растяжения для лопаток являются основными. Они составляют в среднем 50... 70 % общего напряжения. При этом, что очень важно, они действуют по всему сечению лопатки, но не в отдельных точках. Поэтому приближенная оценка лопатки часто производится по напряжениям растяжения, с полным расчетом. Рис. 6.29. Формы колебаний дисков: n — число узловых диаметров; S— число узловых окружностей; 1— узловые диаметры; 2 — узловые окружности. Ко 2-ой группе относятся кососимметричные формы колебания, для которых характерным является наличие только одного узлового диаметра и нескольких узловых окружностей. Для низшей формы колебаний S=0. Особенностью кососимметричных форм колебаний является неуравновешенность динамического момента, возникающего относительно узлового диаметра. 3- тья группа — циклически симметричные формы колебаний. Эта группа весьма обширна, формы колебаний в ней разделяются на подгруппы по числу узловых диаметров:n = 2, 3, 4, 5. Диски роторов компрессоров, когда силовая оболочка ротора проходит по внешнему контуру дисков (рис. 6.32, а), колеблются по формам круглых пластин с заделкой по внешнему контуру. Преобладают формы осесимметричные с различным числом узловых окружностей, но могут быть и с узловыми диаметрами. Диски турбин имеют, как правило, большую ступицу и жесткий пояс крепления к валу (рис. 6.32, г). Колебания таких дисков происходят совместно с лопатками, по формам с несколькими узловыми диаметрами. Пояс заделки диска проходит по поясу крепления к валу.
Рис. 6.29. Формы колебаний дисков: n — число узловых диаметров; S— число узловых окружностей; 1— узловые диаметры; 2 — узловые окружности. Ко 2-ой группе относятся кососимметричные формы колебания, для которых характерным является наличие только одного узлового диаметра и нескольких узловых окружностей. Для низшей формы колебаний S=0. Особенностью кососимметричных форм колебаний является неуравновешенность динамического момента, возникающего относительно узлового диаметра. 3- тья группа — циклически симметричные формы колебаний. Эта группа весьма обширна, формы колебаний в ней разделяются на подгруппы по числу узловых диаметров:n = 2, 3, 4, 5. Диски роторов компрессоров, когда силовая оболочка ротора проходит по внешнему контуру дисков (рис. 6.32, а), колеблются по формам круглых пластин с заделкой по внешнему контуру. Преобладают формы осесимметричные с различным числом узловых окружностей, но могут быть и с узловыми диаметрами. Диски турбин имеют, как правило, большую ступицу и жесткий пояс крепления к валу (рис. 6.32, г). Колебания таких дисков происходят совместно с лопатками, по формам с несколькими узловыми диаметрами. Пояс заделки диска проходит по поясу крепления к валу.

 Лопатки компрессоров и турбин из-за сложности их конструктивной формы не имеют строгого разделения форм колебаний. Колебания лопаток происходят по смешанным формам с преобладанием того или иного вида.
Лопатки компрессоров и турбин из-за сложности их конструктивной формы не имеют строгого разделения форм колебаний. Колебания лопаток происходят по смешанным формам с преобладанием того или иного вида. ; (5.11)
; (5.11) , (5.12)
, (5.12)
 (5.16)
(5.16) (5.17)
(5.17)

 Первые три члена, входящие в формулу (2.1), представляют собой равнодействующие статических давлений, четвертый — динамическое усилие, связанное с изменением осевой скорости воздуха во входном устройстве. Осевой компрессор. Первоначально определяются осевые силы, действующие на каждое рабочее колесо ротора и направляющий аппарат статора. Осевая газодинамическая сила, возникающая на лопатках рабочего колеса, может быть подсчитана по формуле
Первые три члена, входящие в формулу (2.1), представляют собой равнодействующие статических давлений, четвертый — динамическое усилие, связанное с изменением осевой скорости воздуха во входном устройстве. Осевой компрессор. Первоначально определяются осевые силы, действующие на каждое рабочее колесо ротора и направляющий аппарат статора. Осевая газодинамическая сила, возникающая на лопатках рабочего колеса, может быть подсчитана по формуле 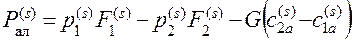 , (2.2)
, (2.2) Где S— верхний индекс — номер ступени; p1, p2, c1a, c2a — статические давления и осевые скорости на cреднем радиусе проточной части перед и за рабочим колесом (рис. 2.6):;. Рис. 2.6. К расчету осевой газодинамической силы лопаток компрессора и турбины
Где S— верхний индекс — номер ступени; p1, p2, c1a, c2a — статические давления и осевые скорости на cреднем радиусе проточной части перед и за рабочим колесом (рис. 2.6):;. Рис. 2.6. К расчету осевой газодинамической силы лопаток компрессора и турбины  Усилие растяжения возрастает от первой ступени к последней, так как происходит сложение осевых сил ступеней. Общее осевое усилие, возникающее на роторе компрессора, равно сумме осевых сил от всех ступеней. Газовая турбина. Осевое усилие, действующее на рабочее колесо турбины и сопловой аппарат, определяется так же, как и для компрессора. Для определения осевого усилия на лопатках может быть использована формула (2.2), в которую подставляются параметры газа и размеры, присущие турбине. Если ротор турбины состоит из нескольких дисков, то подсчет осевой силы такого ротора производится тем же методом, который был рассмотрен для компрессора. Камера сгорания. Осевая газодинамическая сила, действующая на весь узел камеры сгорания в целом, может быть рассчитана по формуле
Усилие растяжения возрастает от первой ступени к последней, так как происходит сложение осевых сил ступеней. Общее осевое усилие, возникающее на роторе компрессора, равно сумме осевых сил от всех ступеней. Газовая турбина. Осевое усилие, действующее на рабочее колесо турбины и сопловой аппарат, определяется так же, как и для компрессора. Для определения осевого усилия на лопатках может быть использована формула (2.2), в которую подставляются параметры газа и размеры, присущие турбине. Если ротор турбины состоит из нескольких дисков, то подсчет осевой силы такого ротора производится тем же методом, который был рассмотрен для компрессора. Камера сгорания. Осевая газодинамическая сила, действующая на весь узел камеры сгорания в целом, может быть рассчитана по формуле  (2.12)
(2.12)





