
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скорости пули с помощью крутильно-Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Баллистического маятника.
Цель работы: определить скорость полета шара с целью практического применения закона сохранения момента импульса, основного уравнения динамики вращательного движения твердого тела, закона сохранения энергии, теоремы Штейнера. Теоретический материал. Вращательное движение твердого тела. Момент силы, момент инерции. Теорема Штейнера, Момент импульса материальной точки, момент импульса твердого тела относительно оси. Уравнение движения твердого тела. Уравнение моментов. Системы материальных точек и моменты сил, которые действуют на систему материальных точек. Закон сохранения момента импульса для замкнутых систем. Потенциальная и кинетическая энергии. Потенциальная энергия упругого взаимодействия. Кинетическая энергия вращающегося твердого тела. Закон сохранения энергии. Консервативные и диссипативные системы. О законах сохранения и неконсервативных системах. Гармонические колебания. Амплитуда, период, частота.
При изучении динамики вращательного движения тел важное значение имеет закон сохранения момента импульса. Моментом импульса частицы относительно точки О называют вектор
Если система частиц замкнута (
Из последнего выражения значит, что моменты импульса отдельных частиц замкнутой системы могут изменяться со временем, однако эти изменения всегда происходят так, что увеличение момента импульса одной части системы равняется уменьшению момента импульса ее другой части. Особый интерес представляют случаи, когда момент импульса В более ограниченном случае у незамкнутых систем может сохраняться не сам момент импульса
надо, что
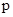 , которые передвигаются, мишенью M и зеркальцем , которые передвигаются, мишенью M и зеркальцем  , подвешенную на стальном проводе (рис.1). При попадании в мишень М шара, который выстреливают из пистолета, маятник отклоняется на некоторый угол a от положения равновесия и начинает совершать гармонические колебания. Период этих колебаний значительно больше времени столкновенья. Угол отклонения маятника от положения равновесия определяется по отклонению светового зайчика, отраженного от зеркальца z на горизонтальной шкале “a” и расстояния от оси вращения маятника до шкалы “b”. Если на зеркальце направить луч света, то при отклонении зеркальца на угол a, отраженный луч повернется на угол 2a, при этом , подвешенную на стальном проводе (рис.1). При попадании в мишень М шара, который выстреливают из пистолета, маятник отклоняется на некоторый угол a от положения равновесия и начинает совершать гармонические колебания. Период этих колебаний значительно больше времени столкновенья. Угол отклонения маятника от положения равновесия определяется по отклонению светового зайчика, отраженного от зеркальца z на горизонтальной шкале “a” и расстояния от оси вращения маятника до шкалы “b”. Если на зеркальце направить луч света, то при отклонении зеркальца на угол a, отраженный луч повернется на угол 2a, при этом  . .
Теория метода. Система маятник-пуля является незамкнутой, поскольку находится в поле сил тяготения. Однако проекция момента силы тяготения на вертикальную ось z равняется нулю, поэтому проекция момента импульса системы маятник-пуля на ось z сохраняется, т.е.
где
Откуда скорость пули равняется:
Массу шара m и расстояние r можно измерить непосредственно. Для определения При ударе шара об маятник последний приобретает кинетическую энергию
где w0 - максимальное значение угловой скорости. По мере закручивания нити кинетическая энергия маятника переходит в потенциальную энергию закручивания нити
Здесь k- модуль кручения, a0 - угол максимального закручивания нити. Считая потери энергии на трение незначительными, по закону сохранения имеем
Последнее выражение дает возможность получить следующее соотношение
Теперь обратимся к основному уравнению динамики вращательного движения и запишем его относительно оси вращения маятника
где
Это линейное однородное дифференциальное уравнение, частинним розв'язком которого является гармоническая функция
Собственная частота гармонических колебаний маятника определяется физическими свойствами колебательной системы и равняется
Соответственно период колебания маятника будет
Учитывая соотношение (2), находим связь между максимальной угловой скоростью маятника w0 и максимальным углом его отклонения a0 при попадании шара
Величины Tи a0могут быть определенные экспериментально. Для определения момента инерции маятника I относительно оси вращения воспользуемся выражением (3), переписав его в виде:
У это соотношение входит модуль кручения нити k, величину которого определить экспериментально тяжело. Чтобы исключить k из дальнейшего рассмотрения воспользуемся следующим приемом. Привинтим к стрежню маятника на расстоянии r1 от оси вращения небольшой шар, который имеет массу m1. Радиус шара должен быть намного меньше r1, тогда момент инерции системы маятник-пуля относительно оси вращения будет
При этом период колебаний маятника изменится и станет T1. С учетом этого можно записать
Разделив (4") на (4), получим
Откуда момент инерции маятника
Подставив теперь значение w0 и I в выражение для скорости пули (1), окончательно находим
Все величины, которые входят в это выражение могут быть легко определенные экспериментально.
Порядок выполнения работы. 1. Взвесить пулю на аналитических весах, а дополнительную пулю на технических. 2. Включить осветитель, привинтить дополнительный шар к стрежню маятника. 3. Отклонить маятник на небольшой угол и отпустить. Измерить время десяти полных колебаний и определить период колебаний маятника с шаром T1.Провести опыт 3 раза и вычислить среднее значение T1. 4. Снять шар и провести аналогичную пункта 3 серию опытов, определив период колебаний маятника T. 5. Вычислить момент инерции маятника по формуле: 6. Сделать выстрел, отмечая по шкале наибольший отброс зайчика “a” и измеряя расстояние “r” от оси вращения до места попадания пули. Опыт повторить 5 раз и найти средние значения “a” и “r”, а также рассчитать границы доверительного интервала Δa, Δr относительно средних значений измеренных величин. 7. По формуле Вычислить w0, используя соотношение 8. По среднему значению измеренных величин рассчитать скорость пули по формуле (5).
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.129.138 (0.012 с.) |

 , который равняется векторному произведению векторов
, который равняется векторному произведению векторов  и
и 
 .
. Вектор
Вектор  и вектор
и вектор  образуют правовинтовую систему. Модуль
образуют правовинтовую систему. Модуль  , где
, где  – плечо вектора
– плечо вектора  , где все вектора определены относительно одной и той же точки О заданной системы отсчета. Закон сохранения момента импульса системы частиц непосредственно вытекает из уравнения моментов
, где все вектора определены относительно одной и той же точки О заданной системы отсчета. Закон сохранения момента импульса системы частиц непосредственно вытекает из уравнения моментов .
. 0), то момент импульса системы остается постоянным, т.е. не изменяется со временем.
0), то момент импульса системы остается постоянным, т.е. не изменяется со временем. .
. 
 всех внешних сил на эту ось
всех внешних сил на эту ось  равняется нулю, то из уравнение
равняется нулю, то из уравнение ,
, .
.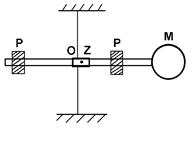 Сам вектор
Сам вектор  и
и  .
. . Момент импульса шара относительно точки О (центр масс маятника) равняется
. Момент импульса шара относительно точки О (центр масс маятника) равняется  и направлен вдоль оси z. В момент столкновения с мишенью вектор
и направлен вдоль оси z. В момент столкновения с мишенью вектор  , где m - масса шара; v - ее скорость; r - расстояние от оси вращения к месту попадания шара в мишень. Испытав неупругий удар с мишенью, система маятник-пуля приобретает угловую скорость
, где m - масса шара; v - ее скорость; r - расстояние от оси вращения к месту попадания шара в мишень. Испытав неупругий удар с мишенью, система маятник-пуля приобретает угловую скорость  , которая направлена вдоль оси z. Поскольку ось вращения маятника является главной осью инерции, то момент импульса системы имеет такой же направление, как и вектор
, которая направлена вдоль оси z. Поскольку ось вращения маятника является главной осью инерции, то момент импульса системы имеет такой же направление, как и вектор 

 - момент инерции шара относительно оси z,
- момент инерции шара относительно оси z,  - момент инерции маятника. Поскольку
- момент инерции маятника. Поскольку  . Соответственно закону сохранения момента импульса системы имеем:
. Соответственно закону сохранения момента импульса системы имеем: .
. (1)
(1) и
и  воспользуемся законом сохранения энергии и основным уравнением динамики вращательного движения.
воспользуемся законом сохранения энергии и основным уравнением динамики вращательного движения.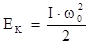 ,
, .
. .
. (2)
(2) ,
, - угловое ускорение маятника, I- момент инерции маятника относительно оси вращения. Получив от шара кинетическую энергию, маятник делает колебание под действием упругого момента нити
- угловое ускорение маятника, I- момент инерции маятника относительно оси вращения. Получив от шара кинетическую энергию, маятник делает колебание под действием упругого момента нити  . Знак минус указывает на то, что упругий момент нити направлен в сторону, противоположную вектору углового перемещения маятника. С учетом этого, основное уравнение динамики вращательного движения можно записать в следующем виде:
. Знак минус указывает на то, что упругий момент нити направлен в сторону, противоположную вектору углового перемещения маятника. С учетом этого, основное уравнение динамики вращательного движения можно записать в следующем виде: = 0.
= 0. .
.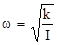 .
.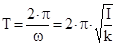 (3)
(3) .
. (4)
(4) .
. (4²)
(4²) .
. .
. (5)
(5)
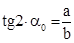 и среднему значению “a” найти a0 в радианах
и среднему значению “a” найти a0 в радианах .
.


